文章目录
- abstract
- 1. introduction
- 2 Related Work
- 2.1 Binary Relation Embedding
- 2.2 Multi-fold Relation Embedding
- 3 Group-Constrained Embedding
- 3.1 Framework
- 3.2 Optimizing Method
- 3.3 Proposed Model
- 3.4 Complexity Analysis
- 4.实验
- 4.1 数据集
- 4.2 Link Prediction
- 4.3 Instance Classification
- 5.总结
Huang, Y., et al. (2019). Group-Constrained Embedding of Multi-fold Relations in Knowledge Bases. Natural Language Processing and Chinese Computing: 235-248.
abstract
知识库的表示学习旨在将实体和关系都嵌入到连续的向量空间中。大多数现有模型(例如TransE,DistMult,ANALOGY和ProjE)仅考虑知识库中涉及的二进制关系,而将多重关系转换为三元组并视为二进制关系的实例,从而导致结构信息丢失。M-TransH是最近提出的用于多重关系的直接建模框架,但忽略了某些事实属于同一关系的关系级信息。本文提出了一种组约束嵌入方法,该方法将实体节点和事实节点从实体空间嵌入到关系空间中,将与同一关系相关的嵌入事实节点限制为具有零约束,半径约束或余弦约束的组。使用此方法,提供了一个新模型,即Gm-TransH。我们在链接预测和实例分类任务上评估了我们的模型,实验结果表明Gm-TransH明显优于以前的多重关系嵌入方法,并取得了出色的性能。
- 实体/关系嵌入(到连续的向量空间中)
- 二元关系:例如TransE,DistMult,ANALOGY和ProjE)
- 多重关系嵌入
- 二元关系的方法用于多重关系(多重关系转化为多个三元组,对每个三元组用二元关系的方法)
- 问题:二元关系的方法若用于多重关系,将之转换为三元组,视为二元关系,导致信息丢失
- 出现谓词的异质性heterogeneity,不利于嵌入
- 解决:M-TransH
- M-TransH的问题:忽略了某些事实属于同一关系的关系级信息
- 解决:本文Gm-TransH
- Gm-TransH:
- 任务:将实体节点和事实节点从实体空间嵌入到关系空间中
- 动机:考虑某些事实属于同一关系的关系级信息
- 做法:以使嵌入的事实向量接近超平面上其对应的关系向量
- 优化:组约束嵌入方法:Group-Constrained Embedding
- 约束:
- 目的:将同一关系的事实节点限制在组中:
- 策略:零约束、半径约束、余弦约束
- 约束:
- 对应于三种策略的三个模型变体:Gm-TransH:zero, Gm-TransH:radius, Gm-TransH:cosine
1. introduction
表示学习[7]已被提出作为一种新的知识库表示和推理方法。它嵌入了实体和实体之间的关系。实体和关系的表示是通过最小化涉及所有实体和关系的全局损失函数获得的。与传统的基于逻辑的推理方法相比,表示学习在语义搜索,问题解答,药物发现和疾病诊断等应用中显示出强大的可行性和鲁棒性。
- 知识图谱应用的方法
- 基于逻辑的推理方法
- 表示学习
- 实体和关系的表示,通过最小化相关的所有实体和关系的全局损失得到
- 更稳定、可行
尽管取得了令人鼓舞的成就,但大多数现有的表示学习技术(例如TransE [1],DistMult [18],ANALOGY [9]和ProjE [12])仅考虑知识库中包含的二元关系,即三元组每个都涉及两个实体和一个关系。例如,“唐纳德·J·特朗普是美国总统”由两个实体组成:“唐纳德·J·特朗普。特朗普”,“美国”和二元关系“一国总统”。但是,我们现实生活中大量的知识是具有多重关系(n元, 2)的实例,在一个实例中涉及三个或更多实体(例如“哈利·波特是英美电影系列根据作者JK罗琳的哈利波特小说”)。解决此问题的通用方法是将每个多重关系转换为具有二进制关系的三元组,并使用现有的Trans(E,H,R)方法学习每个三元组的嵌入。因此,具有N元关系的实例将转换为2)三元组[17]。尽管这种转换能够捕获多重关系结构的一部分[11],但它导致谓词的异质性,不利于嵌入。Wen等。 [17]提倡多重关系的实例表示,并提出了用于知识库嵌入的直接建模框架“ m-TransH”。但是,m-TransH将事实节点与一般实体节点相同,并且忽略某些事实属于同一关系的关系级别信息。
在本文中,我们首先提出了一种组约束嵌入方法,该方法将实体节点和事实节点从实体空间嵌入到关系空间中,使用三种不同的约束策略()将与同一关系相关的嵌入事实节点限制在组中。即零约束,半径约束和余弦约束。
- 数据集
- FB15K [1]
- JF17K [17].
- 贡献:
- Group-Constrained Embedding 框架
- 三种约束策略:零约束,半径约束和余弦约束
- 提出Gm-TransH和三个变体
- 清理冗余数据,从JF17K数据集生成GfactG_{fact}Gfact
(a)提出了用于多重关系嵌入的组约束嵌入框架,该框架将实体和事实节点都嵌入到低维向量空间中,从而迫使事实嵌入接近其对应的关系向量。
(b)我们引入了三种不同的组约束类型:零约束,半径约束和余弦约束。对它们的优缺点进行了经验分析。
(c)整合了TransH模型,并提出了一种新模型Gm-TransH和三个变体Gm-TransH:Zero,Gm-TransH:Radius和GmTransH:Cosine用于多重关系嵌入。链接预测和实例分类任务的实验结果证明了这三种模型变体的有效性。
(d)清理冗余数据并为JF17K数据集生成一个新的子集GfactG_{fact}Gfact。
2 Related Work
2.1 Binary Relation Embedding
- 二元关系
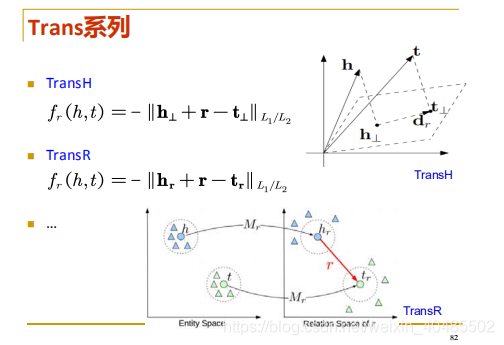
- TransE系列:(transilation embedding)
- TransE:(h,r,t)成立:h+r≈t(h,r,t)成立:h+r\approx t(h,r,t)成立:h+r≈t
- TransH:在不同关系下,实体的表示不同(投影)
- TransR:实体空间–>关系空间
- PTransE [7],
- TranSparse [6],
- KG2E [3]
- MultiKE [19],
- RotatE [14]
- 张量分解方法
- LFM [4],
- HolE [10]
- 神经网络方法
- ProjE [12]
- Conv2D [2],
- NKGE [15],
- CrossE [20]
- TransE系列:(transilation embedding)
2.2 Multi-fold Relation Embedding
- 多重关系嵌入
- 通常使用S2C转换和分解框架[17]
- 多元关系->多个三元组
- 每个三元组用一次二元关系的方法
- 直接的多重关系框架
- M-TransH
- 将TransH直接泛化到multi-fold关系上
- cost function:fr(t)=∣∣Σrho∈M(Rr)ar(ρ)Pnr(t(ρ))+br∣∣22,t∈NM(Rr)M(Rr):涉及关系Rr的一组实体N:KB中的所有实体t::Rr的实例t(ρ):ρ角色的实体Pnr(z):向量z在超平面上的投影,nr:normal向量Pnr(z)=z−nrTznrnr和br:单位长度正交向量f_r(t)=||\Sigma_{rho\in M(R_r)}a_r(\rho)P_{n_r}(t(\rho))+b_r||_2^2,t\in N^{M(R_r)}\\ M(R_r):涉及关系R_r的一组实体\\ N:KB中的所有实体 t::R_r的实例\\ t(\rho):\rho角色的实体\\ P_{n_r}(z):向量z在超平面上的投影,\\n_r:normal向量\\ P_{n_r}(z)=z-n_r^Tzn_r\\ n_r和b_r:单位长度正交向量fr(t)=∣∣Σrho∈M(Rr)ar(ρ)Pnr(t(ρ))+br∣∣22,t∈NM(Rr)M(Rr):涉及关系Rr的一组实体N:KB中的所有实体t::Rr的实例t(ρ):ρ角色的实体Pnr(z):向量z在超平面上的投影,nr:normal向量Pnr(z)=z−nrTznrnr和br:单位长度正交向量
- ar∈RM(Rr),Σrho∈M(Rr)ar(ρ)=0a_r\in R^{M(R_r)},\Sigma_{rho\in M(R_r)}a_r(\rho)=0ar∈RM(Rr),Σrho∈M(Rr)ar(ρ)=0
- M-TransH
- 通常使用S2C转换和分解框架[17]
3 Group-Constrained Embedding
3.1 Framework

- 框架
- 原始文本->知识->知识库中多重关系的实例
- 事实节点:特定关系的每个实例(Fact)
- 实例的实体链接到事实节点(三角形)
- 事实节点可以共享:实体(角色)和关系
- 组:同一个关系的属于一个组
- 组内fact距离近,组间距离远
我们的多重关系建模框架如图1所示。从原始文本中提取的知识构成了知识库中多重关系的实例,我们引入事实节点来表示特定关系的每个实例,并将实例的实体链接到相应的事实节点。这些事实节点可以共享某些角色(即实体)和关系。例如,在图1中,事实2和事实4具有相同的“出生”关系,即唐纳德·特朗普和伊万卡·特朗普都出生在纽约。我们将实体和事实节点都嵌入到低维向量空间中,并使具有相同关系的事实节点的嵌入接近,从而为每种关系类型生成一个组,而使不同关系的组彼此远离。
3.2 Optimizing Method
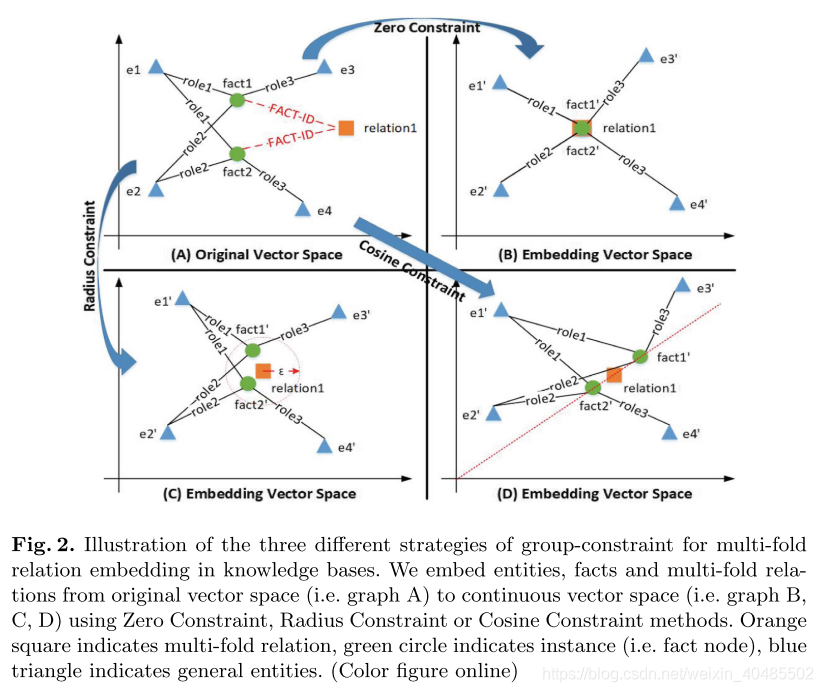
说明了在知识库中进行多重关系嵌入的三种不同的组约束策略。我们使用零约束,半径约束或余弦约束方法将实体,事实和多重关系从原始向量空间(即图A)嵌入到连续向量空间(即图B,C,D)。橙色正方形表示多重关系,绿色圆圈表示实例(即事实节点),蓝色三角形表示一般实体。 (在线彩色图)
将多重关系转换为二进制关系会导致谓词的异构性,这不利于知识库的嵌入。M-TransH [17]将事实节点与一般实体节点相同,忽略了某些事实属于同一关系的关系级别信息。在这里,我们提出了一种称为组约束嵌入的优化方法,该方法将实体节点和事实节点从实体空间嵌入到关系空间中,从而将与同一关系相关的嵌入事实节点限制为特定组。
- 优化方法:组约束嵌入
- 将同一关系相关的嵌入事实节点限定为特定组
- cost function:fr(t)=∣∣Σrho∈M(Rr)ar(ρ)Pnr(t(ρ))+br∣∣22+β×gr(t),t∈NM(Rr)M(Rr):涉及关系Rr的一组实体N:KB中的所有实体t::Rr的实例t(ρ):ρ角色的实体Pnr(z):向量z在超平面上的投影,nr:normal向量Pnr(z)=z−nrTznrnr和br:单位长度正交向量gr(t):用于限制嵌入事实向量和关系向量的惩罚项。前loss,后penalty−−偏置向量br:来代表关系相似度:测量事实嵌入与关系向量的距离f_r(t)=||\Sigma_{rho\in M(R_r)}a_r(\rho)P_{n_r}(t(\rho))+b_r||_2^2+\beta\times g_r(t),t\in N^{M(R_r)}\\ M(R_r):涉及关系R_r的一组实体\\ N:KB中的所有实体 t::R_r的实例\\ t(\rho):\rho角色的实体\\ P_{n_r}(z):向量z在超平面上的投影,\\n_r:normal向量\\ P_{n_r}(z)=z-n_r^Tzn_r\\ n_r和b_r:单位长度正交向量\\ g_r(t):用于限制嵌入事实向量和关系向量的惩罚项。 \\前loss,后penalty-- \\偏置向量b_r:来代表关系 \\相似度:测量事实嵌入与关系向量的距离fr(t)=∣∣Σrho∈M(Rr)ar(ρ)Pnr(t(ρ))+br∣∣22+β×gr(t),t∈NM(Rr)M(Rr):涉及关系Rr的一组实体N:KB中的所有实体t::Rr的实例t(ρ):ρ角色的实体Pnr(z):向量z在超平面上的投影,nr:normal向量Pnr(z)=z−nrTznrnr和br:单位长度正交向量gr(t):用于限制嵌入事实向量和关系向量的惩罚项。前loss,后penalty−−偏置向量br:来代表关系相似度:测量事实嵌入与关系向量的距离
- ar∈RM(Rr),Σrho∈M(Rr)ar(ρ)=0a_r\in R^{M(R_r)},\Sigma_{rho\in M(R_r)}a_r(\rho)=0ar∈RM(Rr),Σrho∈M(Rr)ar(ρ)=0
- 目标:减少损失和惩罚
- 惩罚gr(t)g_r(t)gr(t):(相似度)
- zero-constraint:强约束,令事实向量=关系向量
- gr(t)=∣∣br−Pnr(efact)∣∣2,t∈NM(Rr)g_r(t)=||b_r-P_{n_r}(e_{fact})||_2,t\in N^{M(R_r)}gr(t)=∣∣br−Pnr(efact)∣∣2,t∈NM(Rr)
- 优点:减少解空间,加快模型收敛
- 缺点:降低多样性和表达能力
- 如图B:同组内事实共享相同的实体表示,组内事实表示相同=关系
- radius
- gr(t)=∣∣br−Pnr(efact)∣∣2−ϵ,t∈NM(Rr)g_r(t)=||b_r-P_{n_r}(e_{fact})||_2-\epsilon,t\in N^{M(R_r)}gr(t)=∣∣br−Pnr(efact)∣∣2−ϵ,t∈NM(Rr)
- 宽松的约束,在欧几里得空间的距离<ϵ\epsilonϵ(圆)
- 保证表达能力和多样性
- 缺点:每个维度的贡献均等
- 同组的事实在以关系为中心的圆内(超球体)(图C)
- cosine
- gr(t)=cos(br,Pnr(efact)),t∈NM(Rr)g_r(t)=cos(b_r,P_{n_r}(e_{fact})),t\in N^{M(R_r)}gr(t)=cos(br,Pnr(efact)),t∈NM(Rr)
- 图D:同组在一条线上(过原点)
- zero-constraint:强约束,令事实向量=关系向量
在图A的原始向量空间中,我们有一个三元关系“ relation1”(用橙色正方形表示)和两个实例(用绿色圆圈表示),它们的FACT-ID为“ f act1”和“ f act2”。两个实例中的每个实例都通过不同的角色(即role1,role2和role3)与其他三个通用实体(由蓝色三角形表示)链接。我们在图A中呈现4个一般实体e1,e2,e3和e4。我们可以看到,f act1和f act2在“ role1”和“ role2”上共享相同的实体,这与“ role3”不同。
在图B,C和D中,我们通过在实例和实体的名称上添加单引号来表示实例和实体的嵌入矢量。事实节点“ f act1”的嵌入向量被标记为“ f act1’”。我们指出嵌入的多重关系“ relation1”与原始向量空间中的关系相同,因为它们是相同的向量,并且没有映射操作。
图B显示了具有零约束的组约束嵌入的结果。当我们强制嵌入的事实向量“ f act1’”,“ f act2’”及其对应的关系向量“ relation1”之间的欧几里得距离为零时,这三个向量几乎落入了嵌入向量空间中的同一点。当使用半径约束时,
如图C所示,“ f act1’”和“ f act2’”落入超球体,“ relation1”充当球体的中心,半径ϵ是介于0和0之间的十进制数。 1。我们可以看到,将ϵ设置为0时,半径约束退化为零约束。
在图D中,我们使用余弦距离作为度量,因此嵌入矢量“ f act1’”,“ f act2’”和“ relation1”的角度几乎相同,投影到超平面时落在一条直线上。
3.3 Proposed Model
- Group-constrained m-TransH (Gm-TransH)
- 目标:以使嵌入的事实向量接近超平面上其对应的关系向量
3.4 Complexity Analysis
- 时间复杂度:TransH>Gm-TransH>M-TransH
- 变体:radius>zero>cosine
- 参数数量:Gm-TransH<M-TransH

4.实验
4.1 数据集
- 数据集
- FB15K [1]
- 为了验证我们的模型对特定退化类型的多重(N-ary)关系(N=2)的有效性,我们还对FB15K数据集执行了实例分类任务[1]
- JF17K [17].
- 多重关系:
- T(F):GT(F):GT(F):G
- Tid(F):GidT_{id}(F):G_{id}Tid(F):Gid:缺少大量实例的事实节点
- FACTID:不适用于本文model,去除
- 扩充为GfactG_{fact}Gfact
- 用三元关系表示的二元关系的数据集(S2C(G)):G_{s2c}
- 一致的数据集
- 一开始就去除了冗余
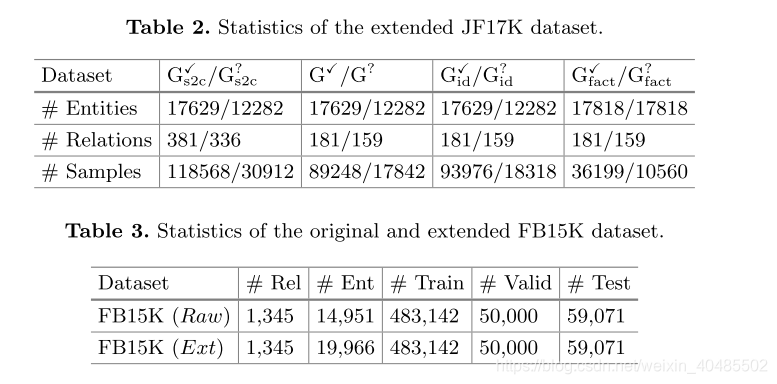
- 多重关系:
- FB15K [1]
FB15K。为了验证我们的模型对特定退化类型的多重(N-ary)关系,即N = 2的二元关系的有效性,我们还对FB15K数据集执行了实例分类任务[1]。由于FB15K数据集仅由三元组的二进制关系组成,并且不包含事实节点的信息,因此我们扩展FB15K数据集并将唯一的事实节点附加到每个三元组。因此,我们可以使用扩展的FB15K数据集训练提出的Gm-TransH模型并在仅保持二进制关系的情况下测试其性能。为了与二进制关系的基准模型进行比较,我们使用原始的FB15K数据集来训练NTN,TransE,TransH和TransR模型。为方便起见,我们使用“ Raw”表示原始FB15K数据集,并使用“ Ext”表示扩展的FB15K数据集。表3列出了原始FB15K和扩展FB15K数据集的统计信息。
4.2 Link Prediction
- 链接预测
- (h,r,t):三缺1,预测缺的部分
- the extended JF17K datasets i
- 给候选实体排序
- Evaluation Protocol
- 将测试集中的实例
- 为了公平起见,我们仅替换实例中出现的真实实体,并排除事实节点。
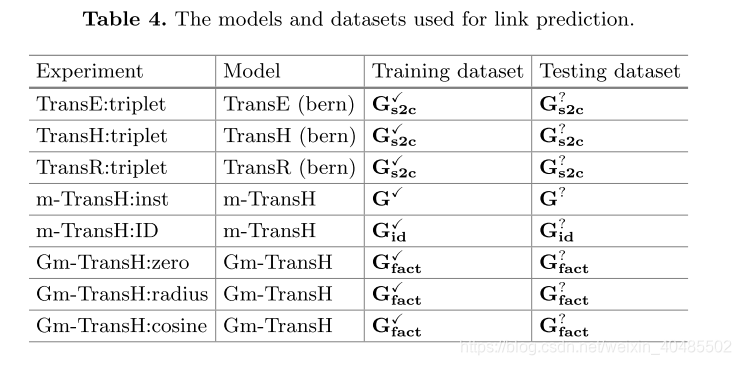
- 参数
按照标准,随机梯度下降用于训练。我们将L2作为相异性,遍历所有训练样本1000轮。在我们的实验中,研究了实体和关系维d的几种选择:25、50、100、150、200、250。我们在0.0015、0.005、0.01、0.1中选择SGD的学习率λ,在0.001、0.01、0.05 0.1中选择Gm-TransH的平衡因子β,在0.5、1.0、2.0中选择余量γ,在Gm-TransH中选择半径ϵ :半径在0.01、0.05、0.1、0.5、1、5之间,批量B在120、480、960、1920之间。三种不同的Gm-TransH模型的最佳配置为Gm-TransH:零:λ= 0.0015,β= 0.01,γ= 0.5,d = 150,B = 960。Gm-TransH:半径:λ= 0.0015,β= 0.05,γ= 1.0,ϵ = 0.05,d = 250,B = 480。Gm-TransH:余弦:λ= 0.0015,β= 0.01,γ= 1.0,d = 200,B = 1920。
- 结果
- 总体而言,模型效果好
- zero:利于判别
- cosine:均值度量上好,具有整体优化能力
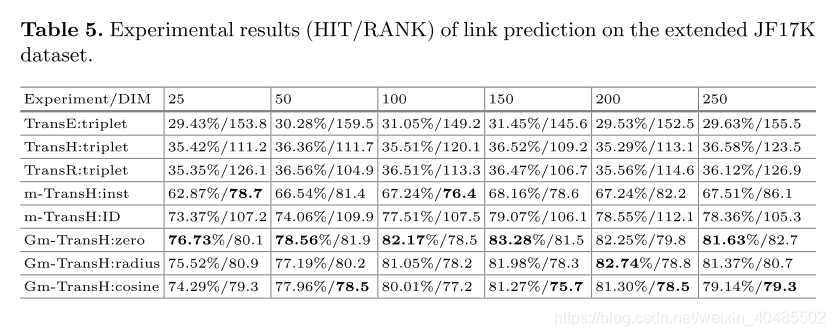
结果。表5中显示了在清洁和扩展的JF17K数据集上进行链接预测的实验结果,该结果显示了尺寸分别为25、50、100、150、200、250的不同嵌入模型的Hit @ 10结果和平均排名结果。这三个Gm-TransH模型在Hit @ 10和平均排名指标上均大大优于Trans(E,H,R)模型。与m-TransH模型相比,我们的模型提高了Hit @ 10的概率,并通过m-TransH:inst获得了近似的平均排名。结果表明,我们的方法对于通过多重关联嵌入提高链接预测的准确性是有效的。此外,相比之下,Gm-TransH:zero优于Hit @ 10度量上的Radius约束和余弦约束,表明Zero Constraint更好用于判别。Gm-TransH:cosine在均值秩度量上表现最佳,并且具有更高的整体优化能力。
4.3 Instance Classification
- 实例分类任务:判断给定实例(h,r,t)是否正确
- 构建否定实例
- 我们选择与链接预测中使用的相同的超参数,并获得20次重复试验的平均准确性。
- 有效
评估协议。对于实例分类任务,我们在NTN和TransH中遵循相同的协议。由于分类的评估需要否定标记,因此JF17K和FB15K数据集都只包含肯定实例,因此我们按照文献[13]中对FB13使用的相同步骤构造否定实例。对于每个黄金实例,都会创建一个否定实例。
通过最大化训练集的分类精度,我们为每个关系r设置阈值。对于测试集中的给定实例,如果相异性得分低于δr\delta_rδr,它将被分类为正,否则为负。
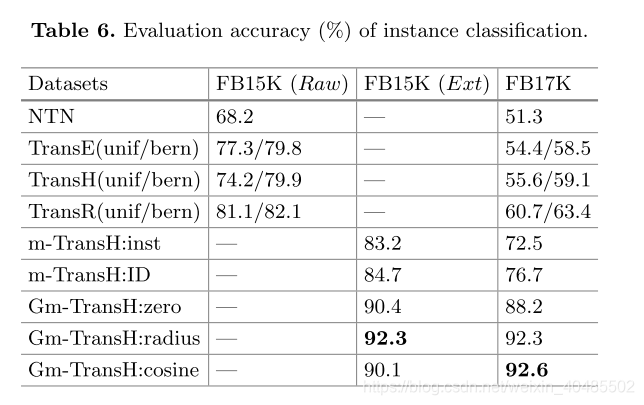
结果。表6详细列出了实例分类的评估结果。我们可以观察到,在FB15K和JF17K数据集上,Gm-TransH模型都可以达到90%的精度,明显优于包括NTN,Trans(E,H,R)和m-TransH在内的基线模型。这表明我们的模型可以有效,富有表现力地学习关系级信息。此外,从FB15K(Raw)和FB15K(Ext)数据集的结果中,我们看到,即使对于二进制关系,组约束嵌入模型也是可行且可靠的。
5.总结
我们提出了具有三种不同类型的多重关系约束策略的群约束嵌入框架,并提出了一种新的表示学习模型Gm-TransH。我们在扩展的FB15K和JF17K数据集上评估所提出模型的有效性和性能。实验结果表明,在链接预测和实例分类任务上,Gm-TransH模型优于所有基线模型。将来,我们将针对知识库中日趋复杂的数据探索更多的表示和嵌入框架,例如事件和过程,并结合了二进制关系学习中的最新进展以进行多重关系嵌入。






,考虑长距离的实体标签之间的关)







)


----内部bean的引入(bean和bean之间的引入)、(3)级联方式注入)

)