原理部分主要来自大牛zouxy09和trnadomeet两个人的博客;后面的代码详细讲解为自己精心编写
一、概述
非监督学习的一般流程是:先从一组无标签数据中学习特征,然后用学习到的特征提取函数去提取有标签数据特征,然后再进行分类器的训练和分类。之前说到,一般的非监督学习算法都存在很多hyper-parameters需要调整。而,最近我们发现对于上面同样的非监督学习流程中,用K-means聚类算法来实现特征学习,也可以达到非常好的效果,有时候还能达到state-of-the-art的效果。亮瞎了凡人之俗眼。
托“bag of features ”的福,K-means其实在特征学习领域也已经略有名气。今天我们就不要花时间迷失在其往日的光芒中了。在这里,我们只关注,如果要K-means算法在一个特征学习系统中发挥良好的性能需要考虑哪些因素。这里的特征学习系统和其他的Deep Learning算法一样:直接从原始的输入(像素灰度值)中学习并构建多层的分级的特征。另外,我们还分析了K-means算法与江湖中其他知名的特征学习算法的千丝万缕的联系(天下武功出少林,哈哈)。
经典的K-means聚类算法通过最小化数据点和最近邻中心的距离来寻找各个类中心。江湖中还有个别名,叫“矢量量化vector quantization”(这个在我的博客上也有提到)。我们可以把K-means当成是在构建一个字典D∊Rnxk,通过最小化重构误差,一个数据样本x(i)∊Rn可以通过这个字典映射为一个k维的码矢量。所以K-means实际上就是寻找D的一个过程:
这里,s(i)就是一个与输入x(i)对应的码矢量。D(j)是字典D的第j列。K-means毕生的目标就是寻找满足上面这些条件的一个字典D和每个样本x(i)对应的码矢量s(i)。我们一起来分析下这些条件。首先,给定字典D和码矢量s(i),我们需要能很好的重构原始的输入x(i)。数学的表达是最小化x(i)和它的重构D s(i)。这个目标函数的优化需要满足两个约束。首先,|| s(i)||0<=1,意味着每个码矢量s(i)被约束为最多只有一个非零元素。所以我们寻找一个x(i)对应的新的表达,这个新的表达不仅需要更好的保留x(i)的信息,还需要尽可能的简单。第二个约束要求字典的每列都是单位长度,防止字典中的元素或者特征变得任意大或者任意小。否则,我们就可以随意的放缩D(j)和对应的码矢量,这样一点用都木有。
这个算法从精神层面与其他学习有效编码的算法很相似,例如sparse coding:
Sparse coding也是优化同样类型的重构。但对于编码复杂度的约束是通过在代价函数中增加一个惩罚项λ|| s(i)||1,以限制s(i)是稀疏的。这个约束和K-means的差不多,但它允许多于一个非零值。在保证s(i)简单的基础上,可以更准确的描述x(i)。
虽然Sparse coding比K-means性能要好,但是Sparse coding需要对每个s(i)重复的求解一个凸优化问题,当拓展到大规模数据的时候,这个优化问题是非常昂贵的。但对于K-means来说,对s(i)的优化求解就简单很多了:
这个求解是很快的,而且给定s求解D也很容易,所以我们可以通过交互的优化D和s(可以了解下我博客上的EM算法的博文)来快速的训练一个非常大的字典。另外,K-means还有一个让人青睐的地方是,它只有一个参数需要调整,也就是要聚类的中心的个数k。
二、数据、数据预处理
2.1数据:
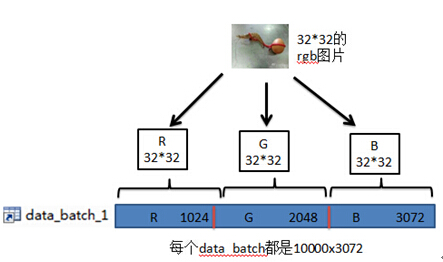
下载的CIFAR-10数据库;其中的每个data_batch都是10000x3072大小的,即有1w个样本图片,每个图片都是32*32且rgb三通道的,这里的每一行表示一个样本。
提取40W个训练patches:
patches = zeros(numPatches, rfSize*rfSize*3);%400000*108
for i=1:numPatches
if (mod(i,10000) ==0) fprintf('Extracting patch: %d / %d\n', i, numPatches);end
r= random('unid', CIFAR_DIM(1) - rfSize +1);%从1到27中采用均匀分布提取数
c= random('unid', CIFAR_DIM(2) - rfSize +1);
%使用mod(i-1,size(trainX,1))是因为对每个图片样本,提取出numPatches/size(trainX,1)=8个patch;每个size(trainX,1)=50000为一轮,提取8轮,总计40W个patches
patch = reshape(trainX(mod(i-1,size(trainX,1))+1, :), CIFAR_DIM);%32*32*3
patch = patch(r:r+rfSize-1,c:c+rfSize-1,:);%6*6*3
patches(i,:) = patch(:)';%patches的每一行代表一个小样本
end
相当于在原始图片上随机抽取8个6*6的rgb 图像patches。
为了建立一个“完备complete”的字典(至少有256个类中心的字典),我们需要保证有足够的用以训练的patches,这样每个聚类才会包含一定合理数量的输入样本。实际上,训练一个k-means字典比其他的算法(例如sparse coding)需要的训练样本个数要多,因为在k-means中,一个样本数据只会贡献于一个聚类的中心,换句话说一个样本只能属于一个类,与其他类就毫无瓜葛了,该样本的信息全部倾注给了它的归宿(对应类的中心)。(以上分析来自zouxy09博客)。所以本文作者用40W个随机patches,来训练108维的聚类特征。
2.2、预处理 Pre-processing
给定多张图片构成的一个矩阵(其中每张图片看成是一个向量,多张图片就可以看做是一个矩阵了)。要对这个矩阵进行whitening操作,而在这之前是需要均值化的。在以前的实验中,有时候是对每一张图片内部做均值,也就是说均值是针对每张图片的所有维度,而有的时候是针对矩阵中图片的每一维做均值操作,那么是不是有矛盾呢?其实并不矛盾,主要是这两种均值化的目的不同。如果是算该均值的协方差矩阵,或者将一些训练样本输入到分类器训练前,则应该对每一维采取均值化操作(因为协方差均值是描述每个维度之间的关系)。如果是为了增强每张图片亮度的对比度,比如说在进行whitening操作前,则需要对图片的内部进行均值化(此时一般还会执行除以该图像内部的标准差操作)。
在训练之前,我们需要对所有的训练样本patches先进行亮度和对比度的归一化。具体做法是,对每个样本,我们减去灰度的均值和除以标准差。另外,在除以标准差的时候,为了避免分母为0和压制噪声,我们给标准差增加一个小的常数。对于[0, 255]范围的灰度图,给方差加10一般是ok的:
样本归一化代码:
patches = bsxfun(@rdivide, bsxfun(@minus,patches, mean(patches,2)), sqrt(var(patches,[],2)+10));
对训练数据进行归一化后,我们就可以在上面运行k-means算法以获得相应的聚类中心了(字典D的每一列),可视化在图a中,可以看到,k-means趋向于学习到低频的类边缘的聚类中心。但不幸的是,这样的特征不会有比较好的识别效果,因为邻域像素的相关性(图像的低频变化)会很强。这样K-means就会产生很多高度相关的聚类中心。而不是分散开聚类中心以更均匀的展开训练数据。所以我们需要先用白化来去除数据的相关性,以驱使K-means在正交方向上分配更多的聚类中心。
图a是由k-means从没有经过白化处理的自然图像中学习到的聚类中心。图b展示了没有和有白化的效果。左边是没有经过白化的,因为数据存在相关性,所以聚类中心会跑偏。右边是经过白化后的,可以看到聚类中心是更加正交的,这样学习到的特征才会不一样。图c展示的是从经过白化后的图像patches学习到的聚类中心。
实现whitening白化一个比较简单的方法是ZCA白化(可以参考UFLDL)。我们先对数据点x的协方差矩阵进行特征值分解cov(x)=VDVT。然后白化后的点可以表示为:
ɛzca是一个很小的常数。对于对比度归一化后的数据,对16x16的patch,可以设ɛzca=0.01,对8x8的patch,可以设ɛzca=0.1 。需要注意的一点是,这个常数不能太小,如果太小会加强数据的高频噪声,会使特征学习更加困难。另外,因为数据的旋转对K-means没有影响,所以可以使用其他的白化变换方法,例如PCA白化(与ZCA不同只在于其旋转了一个角度)。
在白化后的数据中运行k-means可以得到清晰的边缘特征。这些特征和sparse coding啊,ICA啊等等方法学到的初级特征差不多。如图c所示。另外,对于新的数据,可能需要调整归一化的参数ɛ和白化的参数ɛzca,以满足好的效果(例如,图像patches具有高对比度,低噪声和少低频波动)。
数据白化代码:
C = cov(patches);%计算patches的协方差矩阵
M= mean(patches);
[V,D] = eig(C);
P= V * diag(sqrt(1./(diag(D) +0.1))) * V';%P是ZCA Whitening矩阵
%对数据矩阵白化前,应保证每一维的均值为0
patches = bsxfun(@minus, patches, M) * P;%注意patches的行列表示的意义不同时,白化矩阵的位置也是不同的。
三、用kmeans算法获取聚类中心
详见:k-means聚类原理代码分析
四、特征提取
我们用K-means聚类算法来从输入数据中学习K个聚类中心c(k)。当学习到这K个聚类中心后,我们可以有两种特征映射f的方法。第一种是标准的1-of-K,属于硬分配编码:
这个fk(x)表示样本x的特征向量f的第k个元素,也就是特征分量。为什么叫硬分配呢,因为一个样本只能属于某类。也就是说每个样本x对应的特征向量里面只有一个1,其他的全是0。K个类有K个中心,样本x与哪个中心欧式距离最近,其对应的位就是1,其他位全是0,属于稀疏编码的极端情况,高稀疏度啊。
第二种是采用非线性映射。属于软编码。
这里zk=||x-c(k)||2,u(z)是向量z的均值。也就是先计算出对应样本与k个类中心点的平均距离d,然后如果那些样本与类别中心点的距离大于d的话都设置为0,小于d的则用d与该距离之间的差来表示。这样基本能够保证一半以上的特征都变成0了,也是具有稀疏性的,且考虑了更多那些距类别中心距离比较近的值。为什么叫软分配呢。软表示这个样本以一定的概率属于这个类,它还以一定的概率属于其他的类,有点模糊聚类的感觉。而硬则表示这个样本与哪个类中心距离最近,这个样本就只属于这个类。与其他类没有任何关系。
特征提取代码:
1 ,原始图像数据拆分变换:
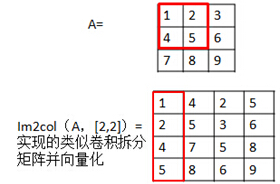
im2col函数:
该函数是将一个大矩阵按照小矩阵取出来,并把取出的小矩阵展成列向量。比如说B =im2col(A,[m n],block_type):就是把A按照m*n的小矩阵块取出,取出后按照列的方式重新排列成向量,然后多个列向量组成一个矩阵。而参数block_type表示的是取出小矩形框的方式,有两种值可以取,分别为’distinct’和’sliding’。Distinct方式是指在取出的各小矩形在原矩阵中是没有重叠的,元素不足的补0。而sliding是每次移动一个元素,即各小矩形之间有元素重叠,但此时没有补0元素的说法。如果该参数不给出,则默认的为’sliding’模式。
代码:
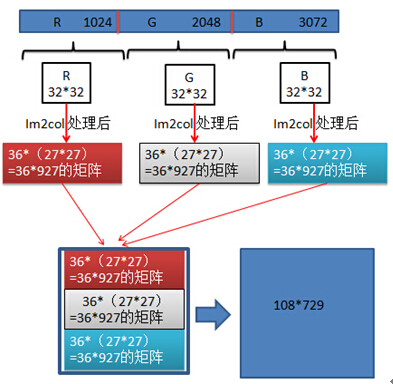
patches = [ im2col(reshape(X(i,1:1024),CIFAR_DIM(1:2)), [rfSize rfSize]) ;
im2col(reshape(X(i,1025:2048),CIFAR_DIM(1:2)), [rfSize rfSize]) ;
im2col(reshape(X(i,2049:end),CIFAR_DIM(1:2)), [rfSize rfSize]) ]';
最后,通过类似“卷积拆分”变换将原始图像变为一个729*108的矩阵,每行为原始图像提取的6*6rgb patch的向量表达;卷积块总共移动729次。
2 ,数据的标准化,白化处理
标准化
patches =
bsxfun(@rdivide,bsxfun(@minus, patches, mean(patches,2)), sqrt(var(patches,[],2)+10));
白化
patches = bsxfun(@minus, patches, M) * P;
3 ,特征提取
此处采用是采用非线性映射,属于软编码。
这里zk=||x-c(k)||2,u(z)是向量z的均值。也就是先计算出对应样本与k个类中心点的平均距离d,然后如果那些样本与类别中心点的距离大于d的话都设置为0,小于d的则用d与该距离之间的差来表示。这样基本能够保证一半以上的特征都变成0了,也是具有稀疏性的,且考虑了更多那些距类别中心距离比较近的值。为什么叫软分配呢。软表示这个样本以一定的概率属于这个类,它还以一定的概率属于其他的类,有点模糊聚类的感觉。而硬则表示这个样本与哪个类中心距离最近,这个样本就只属于这个类。与其他类没有任何关系。
计算样本与k个中心的距离
xx = sum(patches.^2, 2);%729列,的列向量
cc = sum(centroids.^2, 2)';%1600列,的列向量
xc = patches * centroids';%729*1600的矩阵,
z = sqrt( bsxfun(@plus, cc, bsxfun(@minus,xx, 2*xc)) ); % distances = xx^2+cc^2-2*xx*cc;
z为729*1600的矩阵,z矩阵的每行为patches中一行(patches每行为一个rgb卷积块6*6*3=108)与1600个聚类中心的距离。因为一个原始图片有729个卷积块,每个卷积块都与1600个卷积中心计算距离,所以有729*1600个距离。
软编码:
其实就是也就是先计算出对应样本与k个类中心点的平均距离d,然后如果那些样本与类别中心点的距离大于d的话都设置为0,小于d的则用d与该距离之间的差来表示。
这样基本能够保证一半以上的特征都变成0了,也是具有稀疏性的,且考虑了更多那些距类别中心距离比较近的值。
mu = mean(z, 2); % 每个卷积块与1600个中心的平均距离
patches = max(bsxfun(@minus, mu, z), 0);%patches中每一行保存的是:小样本与这1600个类别中心距离的平均值减掉与每个类别中心的距离,限定最小距离为0;
a=[ -1 2 3]; max(a,0)=[0 2 3];%a中的元素与0比较;若小于0,取值为0,大于0取值本身
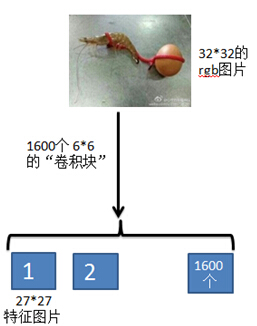
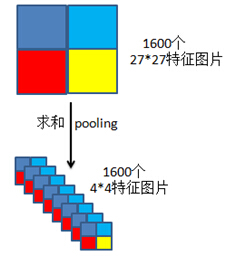
把patches从729*1600,变形为27*27*1600;上面的软编码实现了类似用6*6的卷积块,卷积图像的操作,1600个中心,相当于1600个特征提取卷积块。如图
Patches的每列为:
根据卷积运算图像原则,一个卷积块在原图像上依次滑动,也就是一个特征卷积提取整个图像;按照这个原理,patches的每列应该是每个一个聚类中心点(“卷积块”),与原图像每个卷积模块求距离后,再进行软编码。不应该是上面原图像的每个卷积块,与1600个中心点求距离在进行软计算,这里有些不明白?
4pool操作
prows = CIFAR_DIM(1)-rfSize+1;
pcols = CIFAR_DIM(2)-rfSize+1;
patches = reshape(patches, prows, pcols,numCentroids);
pool代码:
halfr = round(prows/2);
halfc = round(pcols/2);
q1 = sum(sum(patches(1:halfr, 1:halfc, :), 1),2);%区域内求和,是个列向量,1600*1
q2 = sum(sum(patches(halfr+1:end,1:halfc, :), 1),2);
q3 = sum(sum(patches(1:halfr, halfc+1:end, :),1),2);
q4 = sum(sum(patches(halfr+1:end, halfc+1:end, :),1),2);
% concatenate into feature vector
XC(i,:) = [q1(:);q2(:);q3(:);q4(:)]';%类似于pooling操作
这么pool是为了数据降维,但是这是什么pooling方式,为什么用这种方式有些不明白。总之最后向量化后,就提取完特征了。
参考文献:
Deep Learning论文笔记之(三)单层非监督学习网络分析
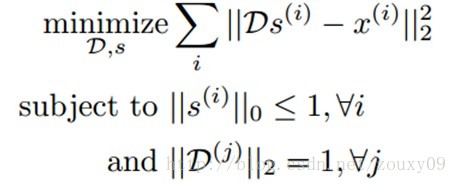
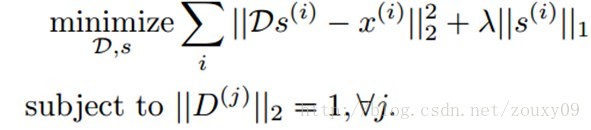
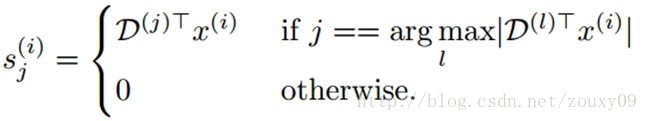

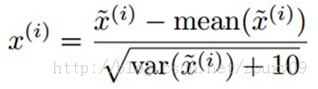

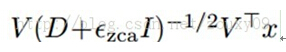
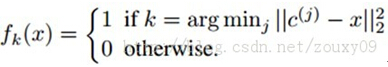
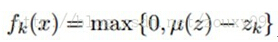
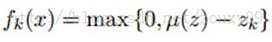




)














