来源：中国科学报

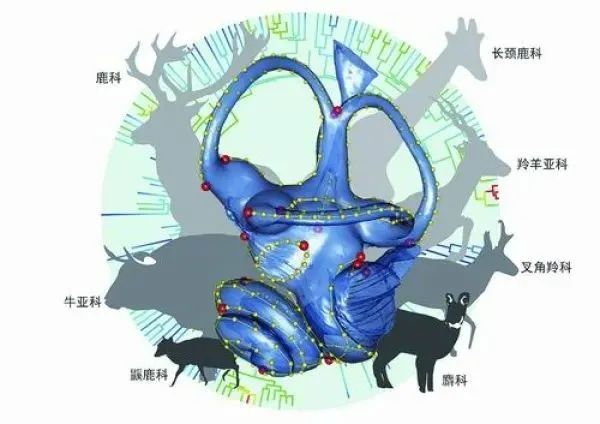
反刍类的内耳几何形态学分析及系统发育示图。Laura Dziomber/绘

化石研究的第一步是通过形态特征鉴定身份，厘清物种的亲缘关系，但这种方法并不完美。那些长相相似的也许“八竿子打不着”，而毫无共同特征的却是“亲属”。

近日，瑞士巴塞尔自然历史博物馆、中国科学院古脊椎动物与古人类研究所（以下简称古脊椎所）等合作团队在《自然-通讯》发表了一项研究成果。他们开创性地找出了一种反刍类动物的形态学特征——内耳迷路，为化石反刍类高阶元系统发育带来全新的研究手段。

姐妹群却没有共同特征

在大型植食性哺乳动物家族里，反刍类是分布最广、多样性最高，也是演化最成功的类群。但让古生物学家头痛的是，反刍类的系统演化关系有着高度的迷惑性。

“这是由于反刍类具有非常广泛的适应性，不同类群在相似的环境选择压力下，强烈呈现出平行或趋同演化的趋势，从而掩盖了系统发育的信息。”古脊椎所研究员王世骐解释说，最典型的例子莫过于叉角羚科。

一开始，研究人员把叉角羚科作为牛科的姐妹群，理由是两者都具有高冠齿。后来，又依据角及头骨的一些共同形态特征，把它们作为鹿科的姐妹群。然而，近年来分子系统发育研究却证实，叉角羚科其实是长颈鹿科的姐妹群。这一结果让科学家大跌眼镜，毕竟这对姐妹群几乎没有什么共同特征。

“分子系统发育的结果往往被认为比传统的形态学手段更加可靠，但运用到古生物学里也有局限性，因为它很难用于时代稍早的化石类群，而反刍类恰恰在新生代具有非常庞大的化石记录，也存在大量的化石科或亚科一级的单元，这也导致了反刍类的高阶分类位置一直都具有很大争议性。”王世骐指出。

因此，找到关键的系统发育和分类学的形态依据，成为古生物学研究的一大挑战。

内耳迷路为高阶元分类提供重要证据

内耳迷路是埋藏在脊椎动物围耳骨中的复杂管状结构，负责平衡和听力的器官就存在于这个结构中。王世骐表示，由于陆生哺乳动物感受平衡的方式和听觉方式早已演化成型，而内耳迷路存在于围耳骨内部，很少受到外界环境选择压力的影响。

“过去对灵长类、食肉类等类群内耳迷路的研究已经证实，它的形态具有很强的系统发育信号，是系统发育重建的有力武器。”王世骐说。

在这项研究中，科研人员利用高分辨率CT三维重建，获得了306件190种现生和化石反刍类的内耳迷路形态三维数据。结果发现，这些反刍类的内耳显示了非常强烈的系统发育信号，尤其在科一级的水平上，这种信号非常明显，与分子重建的系统发育呈现出高度一致性。

王世骐举例说，麝科与牛科的内耳迷路形态接近，而与鹿科有明显区别，从而支持麝科与牛科作为姐妹群组成牛超科，否定了过去通过齿冠高度和蹠骨形态将麝科与鹿科作为姐妹群的观点。

此外，内耳迷路形态还表明，长颈鹿超科、叉角羚科与基干有角类的内耳迷路形态更加接近，支持前两者为各冠群中最先分化出来的类群，这与分子系统发育给出的结果一致。

“这项研究揭示的内耳迷路形态特征，不仅为研究和解决反刍类系统演化和发育难题提供了重要的形态学证据，也为解决一些化石反刍类的分类难题提供了重要的参考依据。”王世骐强调。

相关论文信息：https://doi.org/10.1038/s41467-022-34656-0

未来智能实验室的主要工作包括：建立AI智能系统智商评测体系，开展世界人工智能智商评测；开展互联网（城市）大脑研究计划，构建互联网（城市）大脑技术和企业图谱，为提升企业，行业与城市的智能水平服务。每日推荐范围未来科技发展趋势的学习型文章。目前线上平台已收藏上千篇精华前沿科技文章和报告。

  如果您对实验室的研究感兴趣，欢迎加入未来智能实验室线上平台。扫描以下二维码或点击本文左下角“阅读原文”