递归：

一个问题可以分解成若干子问题，且求解思路一样，当到一定的情况下有终止条件，这样的问题可以用递归方法求解

注意事项：

1. 递归调用深度太大，栈空间会耗尽溢出
2. 注意避免调用中某些值的重复计算（见以下代码3）
3. 递归，频繁调用函数，时间成本高（见以下代码1）
4. 递归代码可以改成循环代码 （见以下代码2）

问题1

给你 n 个台阶，你的最大步幅是2步，可以一次走1步，也可以一次走2步，问有多少种走法？

思路

1. 假设总共走法为 f (n) ，我现在走1步，后面还有 n-1 步（其走法为 f (n-1) ）
2. 我还可以，开始走2步，后面还有 n-2 步（其走法为 f(n-2) ）
3. 那么递推公式即： f (n) = f (n-1) + f (n-2)
4. 终止条件：f (1) = 1; f (2) = 2;

1.递归代码（未考虑重复计算问题）

以下所有代码原来采用 size_t 溢出，改用 unsigned long

#include <iostream>
using namespace std;
unsigned long cal(unsigned long n)
{if(n==1)return 1;else if(n==2)return 2;return cal(n-1)+cal(n-2);
}
int main()
{size_t n;cout << "请输入你要走的台阶数 n :" ;cin >> n;cout << "走台阶有 " << cal(n) << " 种方案。" << endl;return 0;
}

以上递归方法，在 n 比较小的时候运行时间较短
输入 n = 100 时，超过10s还没出结果，我就终止程序了。以下改用循环。

2.循环代码

#include <iostream>
using namespace std;
int main()  //循环
{unsigned long n, step, nextStep = 2, nextnextStep = 1;cout << "请输入你要走的台阶数 n :" ;cin >> n;if(n > 0){if(n == 1){step = 1;} else if(n == 2){step = 2;}else{for(int i = 2; i < n; ++i){step = nextStep + nextnextStep;nextnextStep = nextStep;nextStep = step;}}cout << "走台阶有 " << step << " 种方案。" << endl;}return 0;
}

输入 n = 100 时，改用循环，眨眼间出结果。

3.递归代码（避免重复计算问题）

代码 1 中的 f(n), 比如 n = 5 时

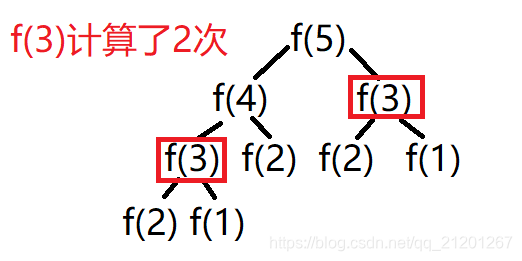
以下代码，屏蔽多次计算重复的值

#include <iostream>
#include <iterator>
#include <map>
using namespace std;
unsigned long cal(unsigned long n, map<unsigned long, unsigned long>& n_fn_map)
{map<unsigned long,unsigned long>::iterator iter = n_fn_map.find(n);   //查找key nif(iter != n_fn_map.end()){return iter->second;    //如果找到了，就不必进行下面计算了，直接返回value}if(n==1){n_fn_map.insert(pair<unsigned long, unsigned long>(1,1)); //把f(1)存入映射return 1;}else if(n==2){n_fn_map.insert(pair<unsigned long, unsigned long>(2,2)); //把f(2)存入映射return 2;}else{size_t sum = cal(n-1,n_fn_map)+cal(n-2,n_fn_map);   //递归调用函数n_fn_map.insert(pair<unsigned long, unsigned long>(n,sum));       //求得的f(n)存入映射，供后面查询直接使用return sum;}
}
int main()  //递归(带避免重复计算fn的值功能)
{size_t n;cout << "请输入你要走的台阶数 n :" ;cin >> n;map<unsigned long, unsigned long> n_Fn;   //n，f(n)的 k，v 容器cout << "走台阶有 " << cal(n,n_Fn) << " 种方案。" << endl;return 0;
}

输入 n = 100，程序也是眨眼间出结果

测试运行时间

测试程序运行时间shell代码：https://blog.csdn.net/qq_21201267/article/details/81840299

问题2

给你 n 个台阶，你的最大步幅是2步，可以一次走1步，也可以一次走2步，先迈左脚，要求最后到达时是右脚，问有多少种走法？

解法1：模拟实际的行走，暴力搜索

/**1. @description: 39个台阶，一次走1步或2步，左脚出发，要求右脚到达2. @author: michael ming3. @date: 2019/4/6 18:174. @modified by: */
#include <iostream>
using namespace std;
void recursion(const unsigned long &targetStairs, unsigned long steps, unsigned long stairsWalkAway, unsigned long &ways)
{		//暴力搜索，n很大时效果不好if(stairsWalkAway > targetStairs)	//走过了，不做记录return;else if(stairsWalkAway == targetStairs && steps%2 == 0)	//正好走到，且步数为偶数（右脚到达）{ways++;	//记录一种方案可以return;}else	//没走到，继续递归{recursion(targetStairs, steps+1, stairsWalkAway+1, ways);recursion(targetStairs, steps+1, stairsWalkAway+2, ways);}
}
int main()
{unsigned long stairs = 0, steps = 0, stairsWalkAway = 0, ways = 0;cout << "请输入台阶个数：" << endl;cin >> stairs;recursion(stairs, steps, stairsWalkAway, ways);cout << "左脚出发，右脚到达的方案有：" << ways << " 种。" << endl;return 0;
}

解法2：递推公式和之前一样，结束条件变了

1. n = 2 时，不论什么情况，大家都只有1种可能，使得右脚到达，f (2) = 1
2. n = 1时，只剩1步了，如果已经走过了偶数步，那就是不可能右脚达到，f(1) = 0；如果已走过奇数步，那也只有1种可能，右脚到达，f(1) = 1
3. 由于 f(1) 是变化的，所以不能用上面问题1的代码3那种方法存储 f(n) 的值，因为其都与 f(1) 相关。所以当 n 比较大的时候还没有找到好的解决办法。

#include <iostream>
#include <map>
using namespace std;
unsigned long cal(size_t n,  size_t stepWalkAway)
{if(n==1){if(stepWalkAway%2 == 0)return 0; //只剩1步了，如果走过了偶数步，那就是右脚达到，不可能了，0return 1;}else if(n==2)   //n = 2 时，不论什么情况，大家都只有1种可能，使得右脚到达{return 1;}else{return cal(n-1,stepWalkAway+1)+cal(n-2,stepWalkAway+1);   //递归调用函数}
}
int main()  
{size_t n, stepWalkAway = 0;cout << "请输入你要走的台阶数 n :" ;cin >> n;cout << "左脚开走，右脚走到有 " << cal(n,stepWalkAway) << " 种方案。" << endl;return 0;
}

解法3：动态规划，现在还不太明白
见他人博客：
https://blog.csdn.net/qq_40269087/article/details/80236102
大概的思路是：自底向上

• 用 left [ i ] 表示剩余 i 个台阶，左脚到达的可能方案， right [ i ] 表示右脚到达的方案
• 边界条件： left [ 1 ] = 1； left [ 2 ] = 1； right [ 1 ] = 0； right [ 2 ] = 1
• 现在还有3个台阶到达，相当于在前面到达的方案中，退一步（1个台阶或者2个台阶），那么我在剩余3个台阶时，左脚到达 left [ 3 ] = right [ 2 ] + right [ 1 ] ；（右脚可以到达的方案，后退一步就变成了左脚到达的方案）
• 同理 right [ 3 ] = left [ 2 ] + left [ 1 ]

#include <iostream>
using namespace std;
unsigned long dynamicProgram(size_t N)
{unsigned long left[N+1], right[N+1];left [1] = 1; left [2] = 1; right [1] = 0; right [2] = 1;for(size_t i = 3; i <= N; ++i){left[i] = right[i-1] + right[i-2];right[i] = left[i-1] + left[i-2];}return right[N];    //题目要求返回右脚到达方案
}
int main()
{size_t N;cout << "请输入你要走的台阶数 n :" ;cin >> N;cout << "左脚开走，右脚走到有 " << dynamicProgram(N) << " 种方案。" << endl;return 0;
}