1. 题目信息

在一个由 0 和 1 组成的二维矩阵内，找到只包含 1 的最大正方形，并返回其面积。

示例:

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/maximal-square
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

类似题目：LeetCode 85. 最大矩形（DP，难）

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {if(matrix.empty())return 0;int i, j, n, incr, maxEdgeLen = 0;int r = matrix.size(), c = matrix[0].size();int dp[r][c];//以右下角为结束的最大正方形边长for(i = 0; i < r; ++i)for(j = 0; j < c; ++j){dp[i][j] = 0;//初始化为0}for(i = 0; i < c; ++i)//第一行填表{if(matrix[0][i] == '1')dp[0][i] = 1;}for(i = 1; i < r; ++i)//第一列填表{if(matrix[i][0] == '1')dp[i][0] = 1;}for(i = 1; i < r; ++i)for(j = 1; j < c; ++j){if(matrix[i][j] == '0')dp[i][j] = 0;else//matrix[i][j] == '1'{n = dp[i-1][j-1];incr = 0;while(n--){incr++;//记录同时为1的次数if(matrix[i-incr][j] == '1' && matrix[i][j-incr] == '1'){continue;//往左和往上同时判断都为1吗？}else//有中断则跳出{incr--;break;}}dp[i][j] = 1+incr;}}for(i = 0; i < r; ++i)for(j = 0; j < c; ++j){if(dp[i][j] > maxEdgeLen)//寻找最大边长maxEdgeLen = dp[i][j];}return maxEdgeLen*maxEdgeLen;//返回最大面积}
};

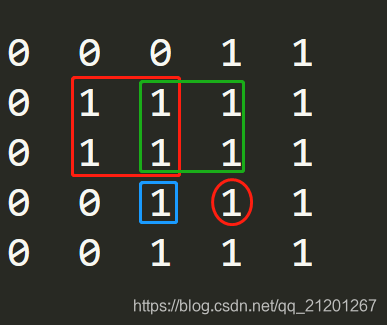
• 又发现以（i，j）为右下角的最大正方形边长 dp[i][j] 就是 min（dp[i-1][j], dp[i][j-1], dp[i-1][j-1]）(i,j 位置左上角3个点的最大边长中的最小者)
  对以上结论，可以自己尝试将1变成0, 0变成1，自己画个图试下。

对上面程序进行小的修改

class Solution {
public:int maximalSquare(vector<vector<char>>& matrix) {if(matrix.empty())return 0;int i, j, n, incr, maxlen = 0;int r = matrix.size(), c = matrix[0].size();int dp[r][c];//以右下角为结束的最大正方形边长memset(dp,0,sizeof(dp));for(i = 0; i < c; ++i)//第一行填表{if(matrix[0][i] == '1')dp[0][i] = 1,maxlen = 1;}for(i = 1; i < r; ++i)//第一列填表{if(matrix[i][0] == '1')dp[i][0] = 1,maxlen = 1;}for(i = 1; i < r; ++i){for(j = 1; j < c; ++j){if(matrix[i][j]=='1'){dp[i][j] = 1+min(dp[i-1][j], min(dp[i][j-1], dp[i-1][j-1]));maxlen = max(maxlen, dp[i][j]);}}}return maxlen*maxlen;}
};