1. Logistic Regression 模型

1.1 logistic 分布

定义：设 $X$ 是连续随机变量， $X$ 服从 logistic 分布是指 $X$ 具有下列分布函数和密度函数：

$F(x)=P(X\le x)=\frac{1}{1+e^{-(x-\mu )/\gamma }}$

$f(x)=F^{\prime }(x)=\frac{e^{-(x-\mu )/\gamma }}{\gamma {(1+e^{-(x-\mu )/\gamma })}^2}$

式中 $\mu$ 为位置参数，$\gamma >0$ 为形状参数

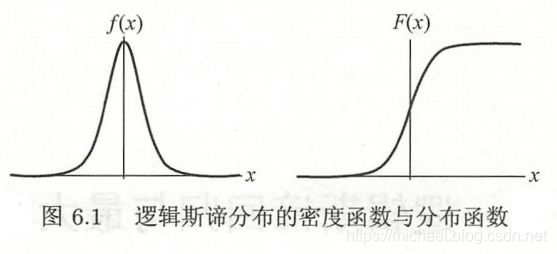
分布函数 $F(x)$ 是一条S形曲线 sigmoid curve，曲线以点 $(\mu ,\frac{1}{2})$ 为中心对称，即满足：$F(-x+\mu )-\frac{1}{2}=-F(x+\mu )+\frac{1}{2}$

形状参数 $\gamma$ 的值越小，曲线在中心附近增长越快

1.2 二项逻辑斯谛回归模型

binomial logistic regression model 是一种分类模型，由条件概率分布 $P(Y|X)$ 表示， 形式为参数化的逻辑斯谛分布。这里，随机变量 $X$ 的取值为实数，随机变量 $Y$ 取值为 1 或者 0。用监督学习的方法来估计模型参数。

二项逻辑斯谛回归模型具有下面条件概率分布：

$P(Y=1|x)=\frac{\exp (wx+b)}{1+\exp (\omega x+b)}$

$P(Y=0|x)=\frac{1}{1+\exp (\omega x+b)}$

$\omega$ 是权值向量，$b$ 是偏置，$\omega \cdot x$ 为 $\omega$ 和 $x$ 的内积（内积，对应位置相乘，再加总）

按照上面式子，可以求得 $P(Y=1|x)$ 和 $P(Y=0|x)$，LR模型将实例 $x$ 分到概率较大的那一类。

事件的几率（odds）是指该事件发生的概率 $p$ 比上 不发生的概率 $1-p$，该事件的对数几率即 $\log it(p)=\log \frac{p}{1-p}$

对于LR来讲，$\log \frac{P(Y=1|x)}{1-P(Y=1|x)}=w\cdot x$，就是说， $Y=1$ 的对数几率是输入 $x$ 的线性函数

1.3 模型参数估计

LR模型学习时，对于给定的训练数据集 T={(x1,y1),(x2,y2),...,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}, 其中，xi∈Rn,yi∈{0,1}x_i \in R^n, \quad y_i \in \{0,1\}xi​∈Rn,yi​∈{0,1}, 应用极大似然估计，得到 LR 模型

假设：$P(Y=1|x)=\pi (x),P(Y=0|x)=1-\pi (x)$

似然函数为：$\prod _{i=1}^N[\pi (x_i){]}^{y_i}[1-\pi (x_i){]}^{1-y_i}$

对数似然函数：
$$\begin{array}{rl}L(\omega )& =\sum _{i=1}^N[y_i\log \pi (x_i)+(1-y_i)\log (1-\pi (x_i))]\\ & =\sum _{i=1}^N[y_i\log \frac{\pi (x_i)}{1-\pi (x_i)}+\log (1-\pi (x_i))]\\ & =\sum _{i=1}^N[y_i(\omega •x_i)-\log (1+\exp (\omega •x_i))]\end{array}$$
对 $L(\omega )$ 求极大值，得到 $\omega$ 的估计值。

1.4 多项逻辑斯谛回归

上面介绍的是两类分类LR模型，可以推广到多类分类。

假设离散随机变量 $Y$ 的取值集合是 {1,2,...,K}\{1,2,...,K\}{1,2,...,K}, 那么多项LR模型是：

$P(Y=k|x)=\frac{\exp ({\omega }_k•x)}{1+\sum _{k=1}^{K-1}\exp ({\omega }_k•x)},k=1,2,...,K-1$

$P(Y=K|x)=\frac{1}{1+\sum _{k=1}^{K-1}\exp ({\omega }_k•x)}$

这里，$x\in R^{n+1},{\omega }_k\in R^{n+1}$ （把 $\omega •x+b$ 合并写做 $\omega •x$，所以 $n$ 维变成 $n+1$ 维）

1.5 Python代码

sklearn.linear_model.LogisticRegression

# -*- coding:utf-8 -*-
# @Python Version: 3.7
# @Time: 2020/3/15 23:27
# @Author: Michael Ming
# @Website: https://michael.blog.csdn.net/
# @File: 6.LogisticRegression_MaxEntropy.py
# @Reference: https://github.com/fengdu78/lihang-codefrom math import exp
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_splitdef create_data():iris = load_iris()df = pd.DataFrame(iris.data, columns=iris.feature_names)df['label'] = iris.targetdata = np.array(df.iloc[:100, [0, 1, -1]])return data[:, :2], data[:, -1]X, y = create_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)class LRclassifier():def __init__(self, max_iter=200, learning_rate=0.01):self.max_iter = max_iterself.learning_rate = learning_rateself.weights = Nonedef sigmoid(self, x):return 1 / (1 + exp(-x))def data_matrix(self, X):data_mat = []for d in X:data_mat.append([1.0, *d])  # 数据加了一个截距项return data_matdef fit(self, X, y):data_mat = self.data_matrix(X)self.weights = np.zeros((len(data_mat[0]), 1), dtype=np.float32)for iter_ in range(self.max_iter):for i in range(len(X)):result = self.sigmoid(np.dot(data_mat[i], self.weights))  # w x 内积error = y[i] - resultself.weights += self.learning_rate * error * np.transpose([data_mat[i]])# 学习算法，更新 wprint('LR Model(learning_rate={},max_iter={})'.format(self.learning_rate, self.max_iter))def score(self, X_test, y_test):right = 0X_test = self.data_matrix(X_test)for x, y in zip(X_test, y_test):result = np.dot(x, self.weights)if (result > 0 and y == 1) or (result < 0 and y == 0):right += 1return right / len(X_test)def predict(self, X_test):result = np.dot(self.data_matrix(X_test), self.weights)if result > 0:return 1else:return 0lr_clf = LRclassifier()
lr_clf.fit(X_train, y_train)
print(lr_clf.score(X_test, y_test))x_points = np.arange(4, 8)
y_ = -(lr_clf.weights[1] * x_points + lr_clf.weights[0]) / lr_clf.weights[2]
plt.plot(x_points, y_)
plt.scatter(X[:50, 0], X[:50, 1], label='0')
plt.scatter(X[50:, 0], X[50:, 1], label='1')
plt.legend()
plt.show()# X_train, y_train = np.array([[3, 3, 3], [4, 3, 2], [2, 1, 2], [1, 1, 1], [-1, 0, 1], [2, -2, 1]]), np.array([1, 1, 1, 0, 0, 0])
# X_test = [[1, 2, -2]]
# lr_clf = LRclassifier()
# lr_clf.fit(X_train, y_train)
# print(lr_clf.predict(X_test))
# ---------sklearn--LR-----------------------
from sklearn.linear_model import LogisticRegressionclf = LogisticRegression(max_iter=200)
clf.fit(X_train, y_train)
print(clf.score(X_test, y_test))
print(clf.coef_, clf.intercept_)
x_ponits = np.arange(4, 8)
y_ = -(clf.coef_[0][0] * x_ponits + clf.intercept_) / clf.coef_[0][1]
plt.plot(x_ponits, y_)
plt.plot(X[:50, 0], X[:50, 1], 'bo', color='blue', label='0')
plt.plot(X[50:, 0], X[50:, 1], 'bo', color='orange', label='1')
plt.xlabel('sepal length')
plt.ylabel('sepal width')
plt.legend()
plt.show()

2. Maximum Entropy 模型

2.1 最大熵原理

• 最大熵原理认为，学习概率模型时，在所有可能的概率模型（分布）中，熵最大的模型是最好的模型。

• 通常用约束条件来确定概率模型的集合，所以，最大熵原理也可以表述为在满足约束条件的模型集合中选取熵最大的模型。

假设离散随机变量 $X$ 的概率分布是 $P(X)$, 则其熵（熵介绍请点击）是：
$H(P)=-\sum _{x}P(x)\log P(x)$

变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。
信息熵是信息论中用于度量信息量的一个概念。一个系统越是有序，信息熵就越低；
反之，一个系统越是混乱，信息熵就越高。

熵满足不等式： $0\le H(P)\le \log |X|$
$|X|$ 是 $X$ 的取值个数，当且仅当 $X$ 是 均匀分布 时右边等号成立；$X$ 均匀分布时（离散较大，混乱，不集中）， 熵最大

最大熵原理认为，要选择的概率模型首先必须满足已有约束条件。在没有更多信息的情况下，那些不确定的部分都是“等可能的 ”。最大熵原理通过熵的最大化来表示等可能性。

2.2 最大熵模型的定义

• 假设分类模型是一个条件概率分布 $P(Y|X)$
• $X\in \mathcal{X}\subseteq R^n$ 表示输入
• $Y\in \mathcal{Y}$ 表示输出，$\mathcal{X},\mathcal{Y}$ 是输入、输出的集合
• 模型：对给定的输入 $X$，以条件概率 $P(Y|X)$ 输出 $Y$
• 训练数据集 T={(x1,y1),(x2,y2),...,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}

---

模型应满足的条件，根据训练集，可以确定联合分布 $P(X,Y)$ 的经验分布

• $\tilde{P}(X=x,Y=y)=\frac{\nu (X=x,Y=y)}{N}$

边缘分布 $P(X)$ 的经验分布

• $\tilde{P}(X=x)=\frac{\nu (X=x)}{N}$，$\nu$ 表示频数，$N$ 表示样本容量

特征函数
$$f(x,y)=\{\begin{array}{r}1,x与y满足某一事实\\ 0,否则\end{array}$$

特征函数 $f(x,y)$ 关于经验分布 $\tilde{P}(X,Y)$ 的期望值：
$E_{\tilde{P}}(f)=\sum _{x,y}\tilde{P}(x,y)f(x,y)$

特征函数 $f(x,y)$ 关于模型 $P(Y|X)$ 与经验分布 $\tilde{P}(X)$ 的期望值：
$E_P(f)=\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)$

如果模型能够获取训练数据中的信息，那么就可以假设这两个期望值相等，即
$E_P(f)=E_{\tilde{P}}(f)$
$\sum _{x,y}\tilde{P}(x)P(y|x)f(x,y)=\sum _{x,y}\tilde{P}(x,y)f(x,y)$

将上式作为模型学习的约束条件。如果有 $n$ 个特征函数 $f_i(x,y)$ ，就有 $n$ 个约束条件。

---

最大熵模型（定义）:

• 假设满足所有约束条件的模型集合为：
  C≡{P∈P∣EP(fi)=EP~(fi),i=1,2,...,n}\mathcal{C} \equiv \{P \in \mathcal{P} | E_P(f_i)=E_{\tilde P}(f_i),i=1,2,...,n\}C≡{P∈P∣EP​(fi​)=EP~​(fi​),i=1,2,...,n}
• 定义在条件概率分布 $P(Y|X)$ 上的条件熵为：
  $H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$
• 则模型集合 $\mathcal{C}$ 中条件熵 $H(P)$ 最大的模型称为最大熵模型，对数为自然对数 $e$

2.3 最大熵模型的学习

学习过程就是约束最优化问题。

对于给定的训练数据集 T={(x1,y1),(x2,y2),...,(xN,yN)}T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，以及特征函数 $f_i(x,y),i=1,2,...,n$，ME 模型的学习等价于约束最优化问题：

$\underset{P\in \mathcal{C}}{\max }H(P)=-\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$
$s.t.E_P(f_i)=E_{\tilde{P}}(f_i),i=1,2,...,n$
$\sum _{y}P(y|x)=1$

按照最优化的习惯，改为求最小值问题：

$\underset{P\in \mathcal{C}}{\min }-H(P)=\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)$
$s.t.E_P(f_i)-E_{\tilde{P}}(f_i)=0,i=1,2,...,n$
$\sum _{y}P(y|x)=1$

---

求解：

引进拉格朗日乘子 ${\omega }_0,{\omega }_1,{\omega }_2,...,{\omega }_n$，定义拉格朗日函数 $L(P,\omega )$ ：

$$\begin{array}{rl}L(P,\omega )& \equiv -H(P)+{\omega }_0(1-\sum _{y}P(y|x))+\sum _{i=1}^n{\omega }_i(E_{\tilde{P}}(f_i)-E_P(f_i))\\ & =\sum _{x,y}\tilde{P}(x)P(y|x)\log P(y|x)+{\omega }_0(1-\sum _{y}P(y|x))+\\ & \sum _{i=1}^n{\omega }_i(\sum _{x,y}\tilde{P}(x,y)f_i(x,y)-\sum _{x,y}\tilde{P}(x)P(y|x)f_i(x,y))\end{array}$$
通过求解对偶问题求解原始问题。

最优化原始问题：$\underset{P\in \mathcal{C}}{\min }\underset{\omega }{\max }L(P,\omega )$

对偶问题：$\underset{\omega }{\max }\underset{P\in \mathcal{C}}{\min }L(P,\omega )$

---

先求对偶问题内部的极小化问题 $\underset{P\in \mathcal{C}}{\min }L(P,\omega )$, $\underset{P\in \mathcal{C}}{\min }L(P,\omega )$ 是 $\omega$ 的函数，记为：
$\Psi (\omega )=\underset{P\in \mathcal{C}}{\min }L(P,\omega )=L(P_{\omega },\omega )$, 称为对偶函数
对偶函数的解记为：$P_{\omega }=\underset{P\in \mathcal{C}}{\mathrm{argmin}}L(P,\omega )=P_{\omega }(y|x)$

$L(P,\omega )$ 对 $P(y|x)$ 求偏导数：

$$\begin{array}{rl}\frac{\partial L(P,\omega )}{\partial P(y|x)}& =\sum _{x,y}\tilde{P}(x)(\log P(y|x)+1)-\sum _y{\omega }_0-\sum _{x,y}(\tilde{P}(x)\sum _{i=1}^n{\omega }_i{f}_i(x,y))\\ & =\sum _{x,y}\tilde{P}(x)(\log P(y|x)+1-{\omega }_0-\sum _{i=1}^n{\omega }_i{f}_i(x,y))\end{array}$$

令偏导数等于0，在 $\tilde{P}(x)>0$ 的情况下，有

$P(y|x)=\exp (\sum _{i=1}^n{\omega }_i{f}_i(x,y)+{\omega }_0-1)=\frac{\exp (\sum _{i=1}^n{\omega }_i{f}_i(x,y))}{\exp (1-{\omega }_0)}$

由于 $\sum _{y}P(y|x)=1$, 得

$P_{\omega }(y|x)=\frac{1}{Z_{\omega }(x)}\exp (\sum _{i=1}^n{\omega }_i{f}_i(x,y)),其中Z_{\omega }(x)=\sum _y\exp (\sum _{i=1}^n{\omega }_i{f}_i(x,y))$

$Z_{\omega }(x)$ 是规范化因子； $f_i(x,y)$ 是特征函数；${\omega }_i$ 是特征的权值。
红色部分就是最大熵模型，$\omega$ 是ME模型中的参数向量。

---

再求解对偶问题外部的极大化问题 $\underset{\omega }{\max }\Psi (\omega )$
其解记为 ${\omega }^{\ast }$, ${\omega }^{\ast }=\underset{\omega }{\mathrm{argmax}}\Psi (\omega )$

应用最优化算法求对偶函数 $\Psi (\omega )$ 的极大化， 得到 ${\omega }^{\ast }$, 用来表示 $P^{\ast }\in \mathcal{C}$, 这里 $P^{\ast }=P_{{\omega }^{\ast }}=P_{{\omega }^{\ast }}(y|x)$ 是学习到的最优模型（最大熵模型）。

2.4 例题

假设随机变量 $X$ 有5个取值 {A,B,C,D,E}\{A,B,C,D,E\}{A,B,C,D,E},要估计各个值的概率 $P(A),P(B),P(C),P(D),P(E)$，其中 $P(A)+P(B)=\frac{3}{10}$，求最大熵模型。

解：

用 $y_1,y_2,y_3,y_4,y_5$ 表示 $A,B,C,D,E$,最大熵模型学习的最优化问题是：

$\min -H(P)=\sum _{i=1}^{5}P(y_i)\log P(y_i)$
$s.t.P(y_1)+P(y_2)=\tilde{P}(y_1)+\tilde{P}(y_2)=\frac{3}{10}$
$\sum _{i=1}^{5}P(y_i)=\sum _{i=1}^5\tilde{P}(y_i)=1$

• 引进拉格朗日乘子 ${\omega }_0,{\omega }_1$ , 定义拉格朗日函数：

$L(P,\omega )=\sum _{i=1}^{5}P(y_i)\log P(y_i)+{\omega }_1(P(y_1)+P(y_2)-\frac{3}{10})+{\omega }_0(\sum _{i=1}^{5}P(y_i)-1)$

根据拉格朗日对偶性，可以通过求解对偶最优化问题得到原始最优化问题的解，所以求解：$\underset{\omega }{\max }\underset{P}{\min }L(P,\omega )$

• 求解 $L(P,\omega )$ 关于 $P$ 的极小化问题，求偏导：

$$\begin{array}{rl}\frac{\partial L(P,\omega )}{\partial P(y_1)}& =1+\log P(y_1)+{\omega }_1+{\omega }_0\\ \frac{\partial L(P,\omega )}{\partial P(y_2)}& =1+\log P(y_2)+{\omega }_1+{\omega }_0\\ \frac{\partial L(P,\omega )}{\partial P(y_3)}& =1+\log P(y_3)+{\omega }_0\\ \frac{\partial L(P,\omega )}{\partial P(y_4)}& =1+\log P(y_4)+{\omega }_0\\ \frac{\partial L(P,\omega )}{\partial P(y_5)}& =1+\log P(y_5)+{\omega }_0\end{array}$$

• 令各偏导数等于0，解得：
  $$\begin{array}{rl}P(y_1)& =P(y_2)=e^{-{\omega }_1-{\omega }_0-1}\\ P(y_3)& =P(y_4)=P(y_5)=e^{-{\omega }_0-1}\end{array}$$

于是：
$\underset{P}{\min }L(P,\omega )=L(P_{\omega },\omega )=-2e^{-{\omega }_1-{\omega }_0-1}-3e^{-{\omega }_0-1}-\frac{3}{10}{\omega }_1-{\omega }_0$

• 再求解 $L(P_{\omega },\omega )$ 关于 $\omega$ 的极大化问题：

$\underset{\omega }{\max }L(P_{\omega },\omega )=-2e^{-{\omega }_1-{\omega }_0-1}-3e^{-{\omega }_0-1}-\frac{3}{10}{\omega }_1-{\omega }_0$
上式对 ${\omega }_0,{\omega }_1$求偏导数并令其等于0，有：
$e^{-{\omega }_1-{\omega }_0-1}=\frac{3}{20}$
$e^{-{\omega }_0-1}=\frac{7}{30}$

于是求得概率分布：
$$\begin{array}{rl}P(y_1)& =P(y_2)=\frac{3}{20}\\ P(y_3)& =P(y_4)=P(y_5)=\frac{7}{30}\end{array}$$

3. 模型学习的最优化算法

常用的方法有 改进的迭代尺度法、梯度下降法、牛顿法或拟牛顿法。牛顿法或拟牛顿法一般收敛速度更快。
（略）

4. 鸢尾花LR分类实践

基于sklearn的LogisticRegression二分类实践

基于sklearn的LogisticRegression鸢尾花多类分类实践