1. 题目

给定一个整数数组 A，对于每个整数 A[i]，我们可以选择 x = -K 或是 x = K，并将 x 加到 A[i] 中。

在此过程之后，我们得到一些数组 B。

返回 B 的最大值和 B 的最小值之间可能存在的最小差值。

示例 1：
输入：A = [1], K = 0
输出：0
解释：B = [1]示例 2：
输入：A = [0,10], K = 2
输出：6
解释：B = [2,8]示例 3：
输入：A = [1,3,6], K = 3
输出：3
解释：B = [4,6,3]提示：
1 <= A.length <= 10000
0 <= A[i] <= 10000
0 <= K <= 10000

来源：力扣（LeetCode） 链接：https://leetcode-cn.com/problems/smallest-range-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

类似题目：LeetCode 908. 最小差值 I

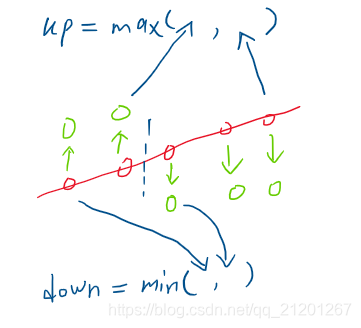
• 首先 都向一侧偏移，差值就是max-min
• 部分偏移的话，排序以后，左侧小的+K，右侧大的-K，才可能得到更小的差值
• 遍历所有的分割点
  

class Solution { // c++
public:int smallestRangeII(vector<int>& A, int K) {sort(A.begin(), A.end());int i, n = A.size(), up, down;int mindis = INT_MAX;for(i = 0; i < n-1; i++){up = max(A[i]+K, A[n-1]-K);down = min(A[0]+K, A[i+1]-K);mindis = min(mindis, up-down);}return min(mindis, A[n-1]-A[0]);//第二种情况为同侧偏置}
};

68 ms 15 MB

class Solution: # py3def smallestRangeII(self, A: List[int], K: int) -> int:A.sort()mindis = float("inf")n = len(A)for i in range(n-1):up = max(A[i]+K, A[n-1]-K)down = min(A[0]+K, A[i+1]-K)mindis = min(mindis, up-down)return min(mindis, A[n-1]-A[0])# 第二种情况为同侧偏置

212 ms 14.9 MB