时间序列简单的说就是各时间点上形成的数值序列，通过观察历史数据的变化规律预测未来的值。在这里需要强调一点的是，时间序列分析并不是关于时间的回归，它主要是研究自身的变化规律的。

准备工作：SPSS - 中文版 SPSS 22.0 软件下载与安装教程 - 【附产品授权许可码，永久免费】

第一步：导入数据

路径：【文件】--【打开】--【数据】--【更改文件类型，找到你的数据】--【打开】--【然后会蹦出下图左中的筛选框，基本使用默认值就行，点确定】

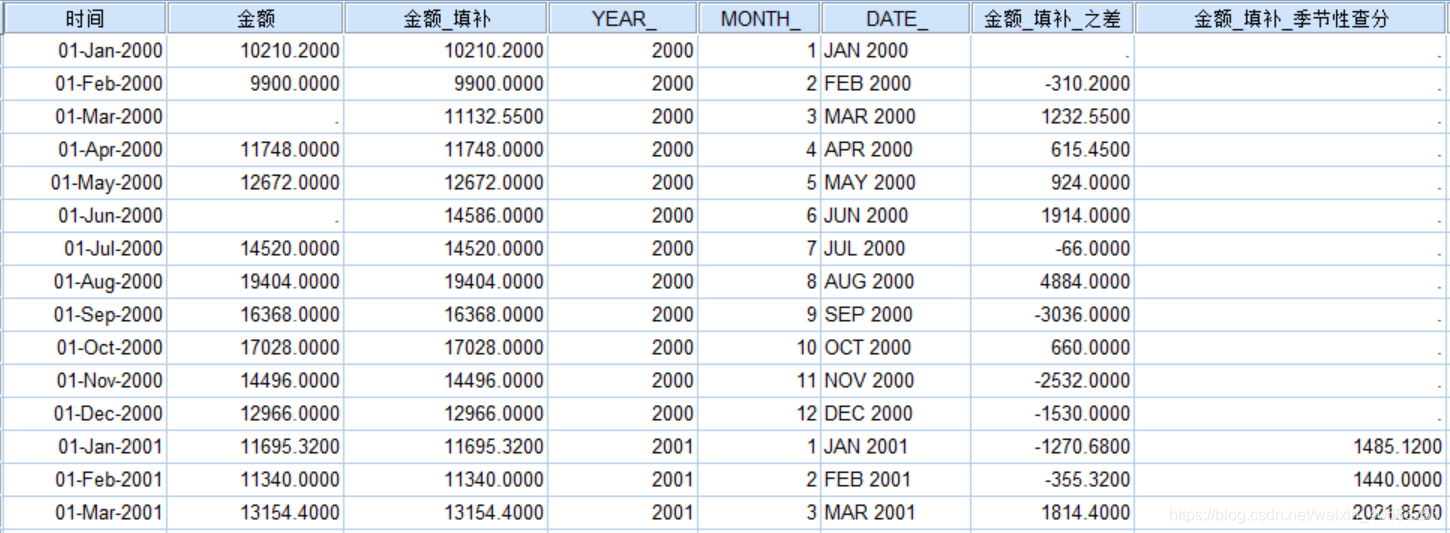
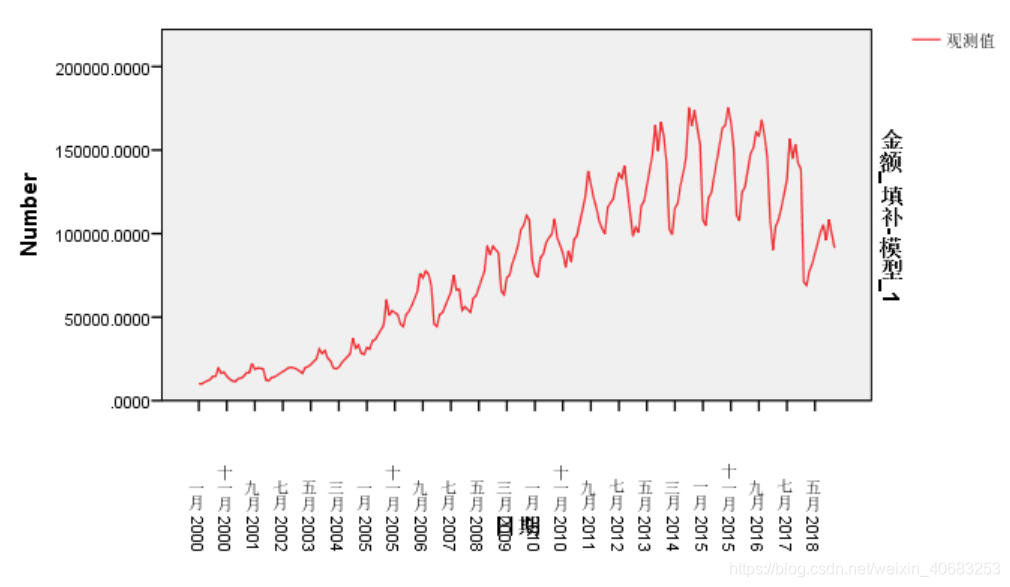
数据中，第一列为融资年月时间（2000-01~2018-12），第二列为融资金额（已脱敏），一共228行数据。

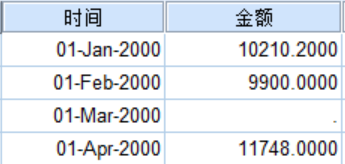
既然是研究融资金额在各时间点上的变化规律，那么第一列的月份必须连续，因此部分月份会有缺失值存在。下面我们需要填补缺失值。

第二步：数据预处理

填补缺失值：

【转换】--【替换缺失值】

【1：选择存在缺失值的列名（金额）】--【2：点击箭头】--【3：重命名填补缺失值之后的列名】--【4：选择填补缺失值的方法】--【5：部分填补方法需要设置邻近点的跨度】--【6：所有方法设置好了之后，点击更改（勿忘）】--【7：点击确定】

         

共有7个缺失值被邻近点的均值替换，填补之后的数据表为下图右所示。

时间变量的定义：

 若需要按照月度（或年度）差分查看分布状况的话，我们还需要对时间列进行转换。

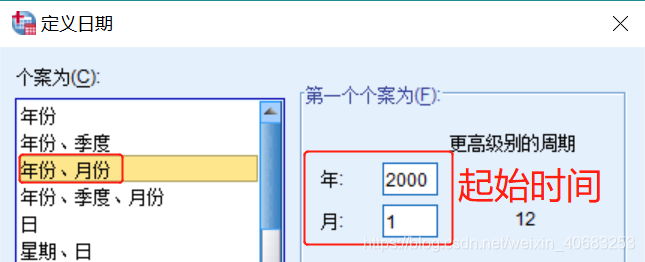
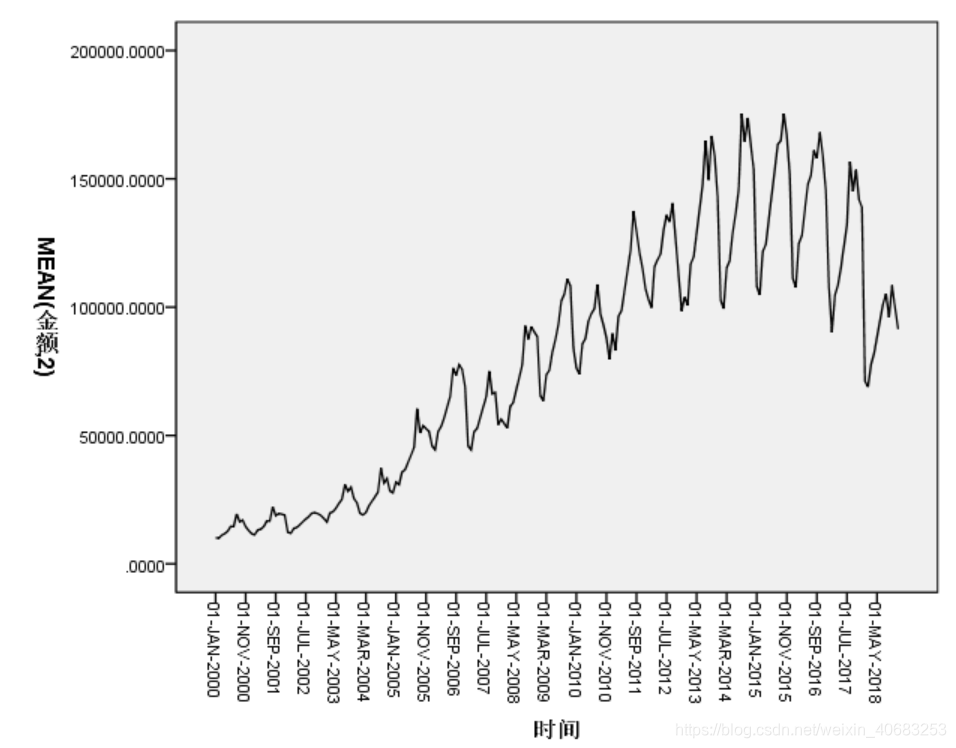
第三步：做图观察

【分析】--【预测】--【序列图】

【变量（y轴，使用填补缺失值后的金额）】--【时间轴标签（x轴）】--【待熟悉之后可以尝试改变‘时间线’、‘格式’、‘转换’里的参数，现在先使用默认值】--【确定】

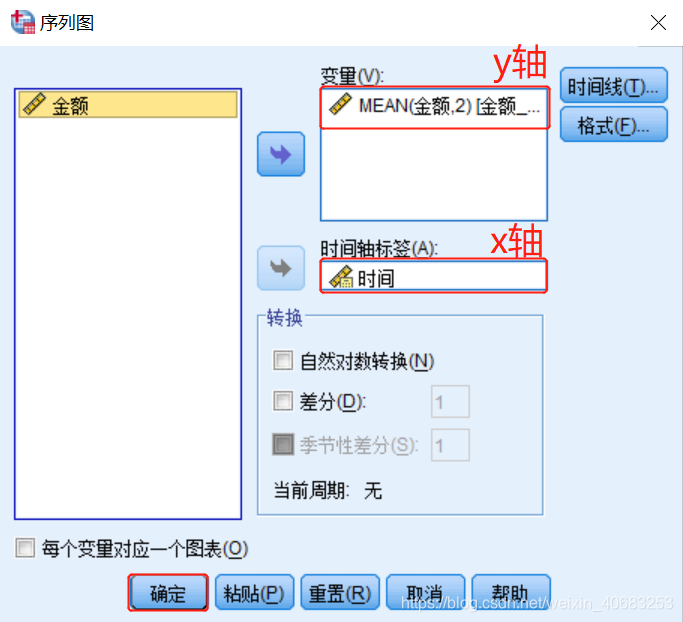
输出：大致可以看出，金额随着时间的变化是有一定规律的。

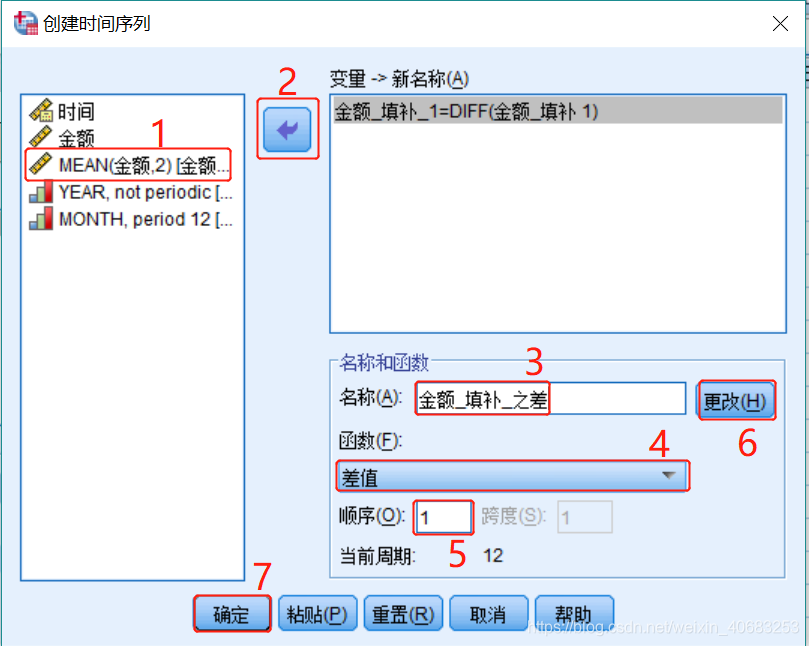
第四步：创建时间序列

计算前后相邻两个数值之差

输出：

 给‘金额_填补_之差’这一列作图观察数值的变化情况（操作步骤与第三步一样）：

图形输出：

如果每个月金额的变化速度一致的话（即接近等差数列），那么‘金额_填补_之差’这一列的数值应该是比较平缓的！

季节差分

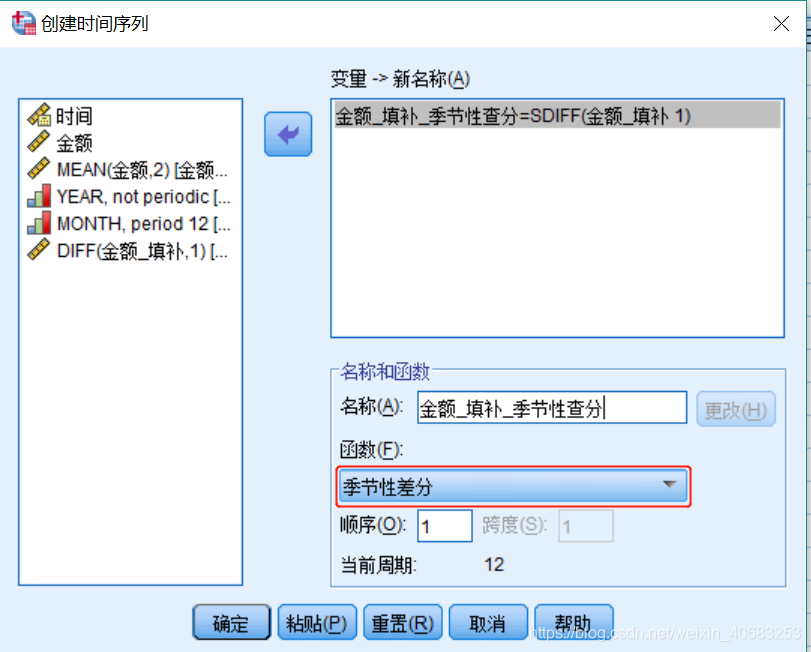
输出：

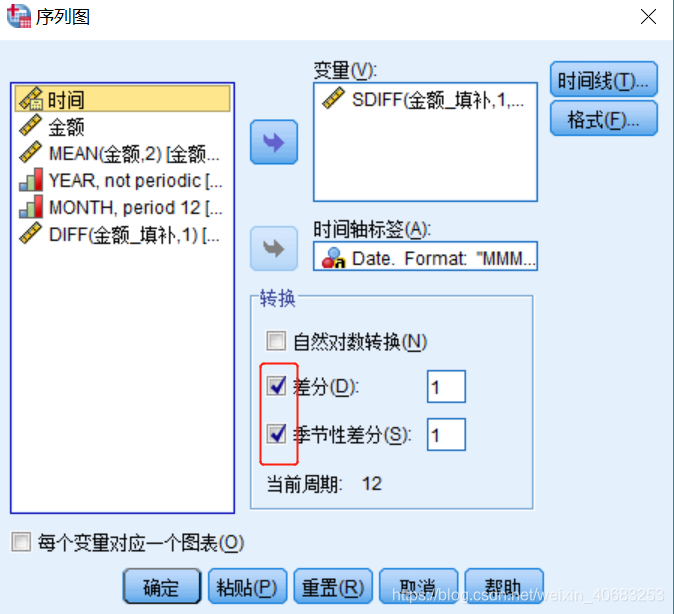
 给‘金额_填补_季节性查分’这一列作图观察数值的变化情况（操作步骤与第三步的区别是，需要勾选【差分】和【季节性差分】如下图所示）：

图形输出：

 第五步：自相关分析

通过自相关看金额变量在时间上是否存在序列依存性。

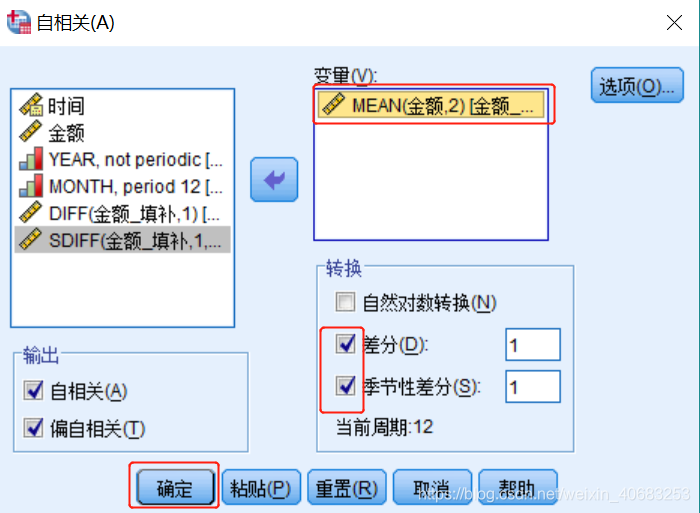
输出结果：

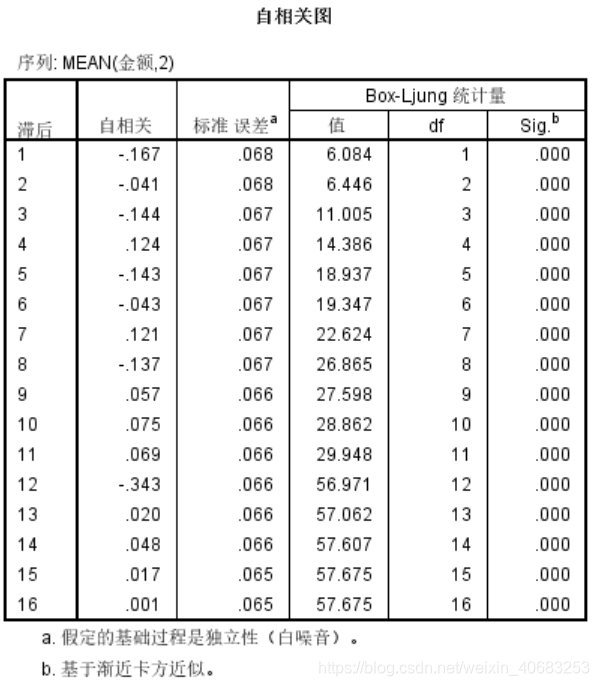
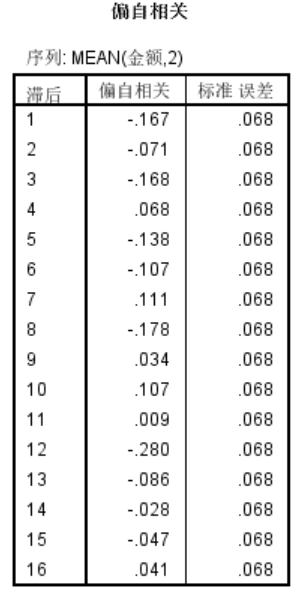
自相关图中，Sig 小于理论显著性水平 0.01（或0.05） 即认为显著，这些数据间是有自相关的。

第六步：创建模型

【分析】--【预测】--【创建模型】

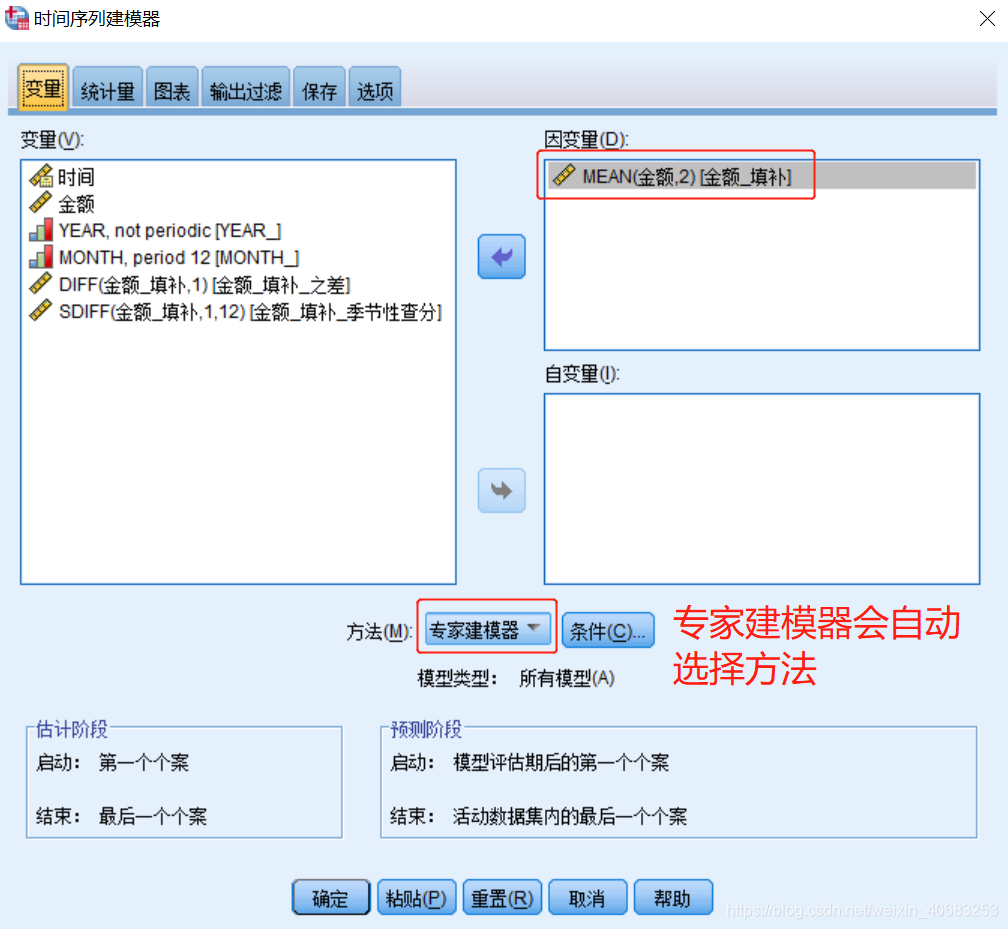
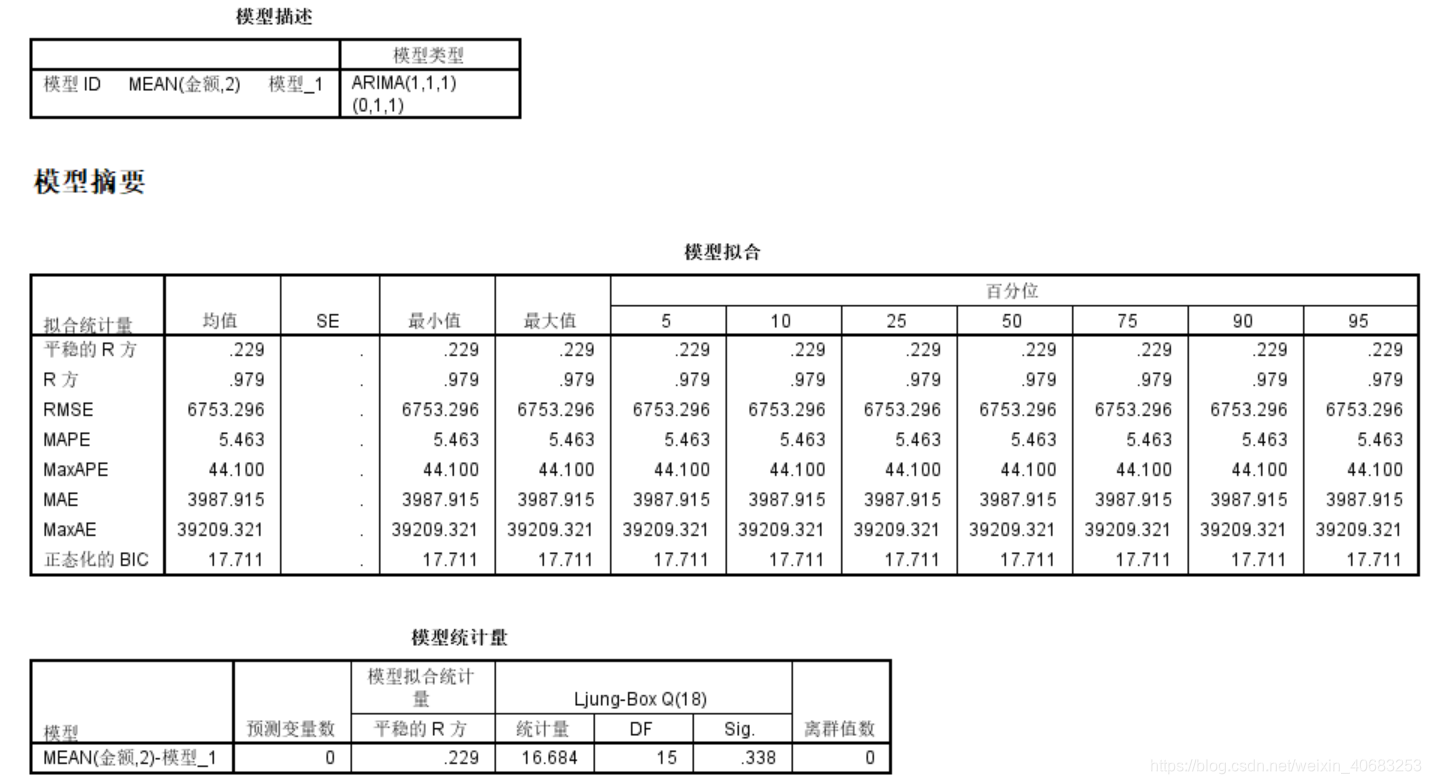
输出：

平稳的R方：决定系数，现有模型所能够解释的原变量的多少变异（较客观）。

R方：原数据去掉季节趋势，波动趋势，周期趋势之后的变异解释度（偏高）。

RMSE：残差均方。

MAPE：平均相对误差。

MAXApe：最大的相对百分比误差。

MAE：平均实测误差。

MAXAE：最大的绝对误差

H0未被拒绝。H0:当前的模型剩下来的这一块是否被看成是白噪声序列。

保存模型：【分析】--【预测】--【创建模型】

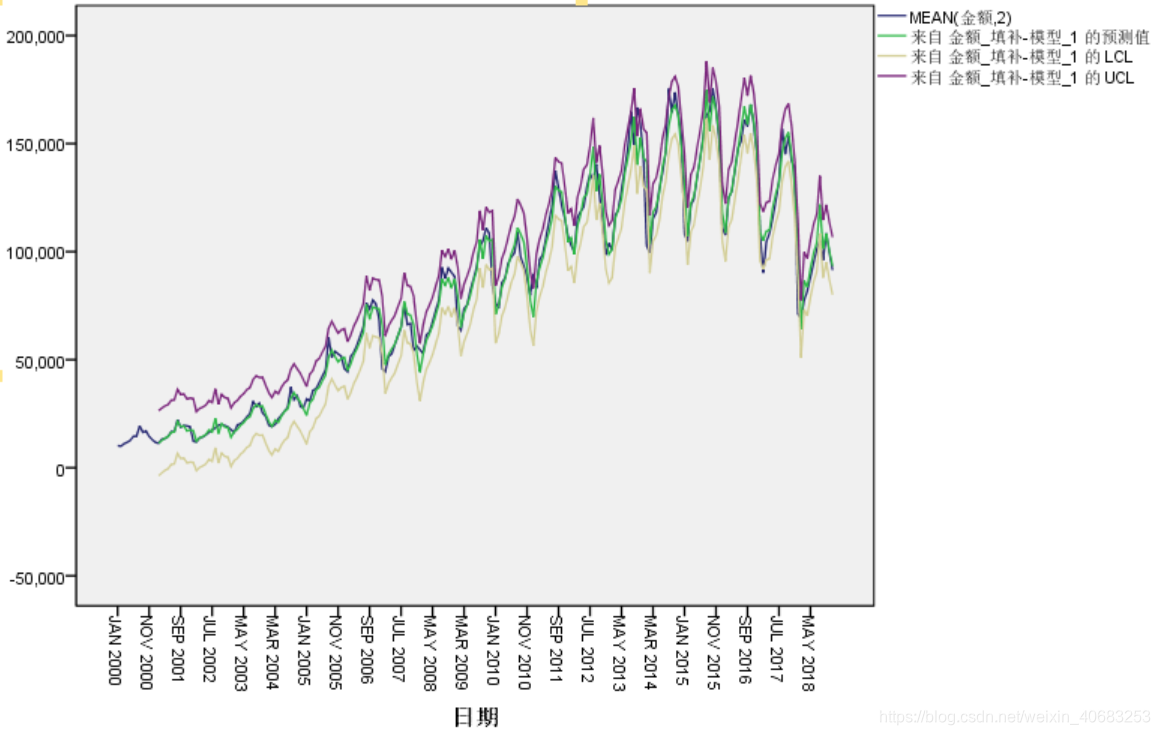
 对比预测值与实际值：

按照第三步的操作（区别是 y 轴不仅仅是填充后的金额第一列，还需要选上 以 pre，LCL，UCL为前缀的三列）进行对比：

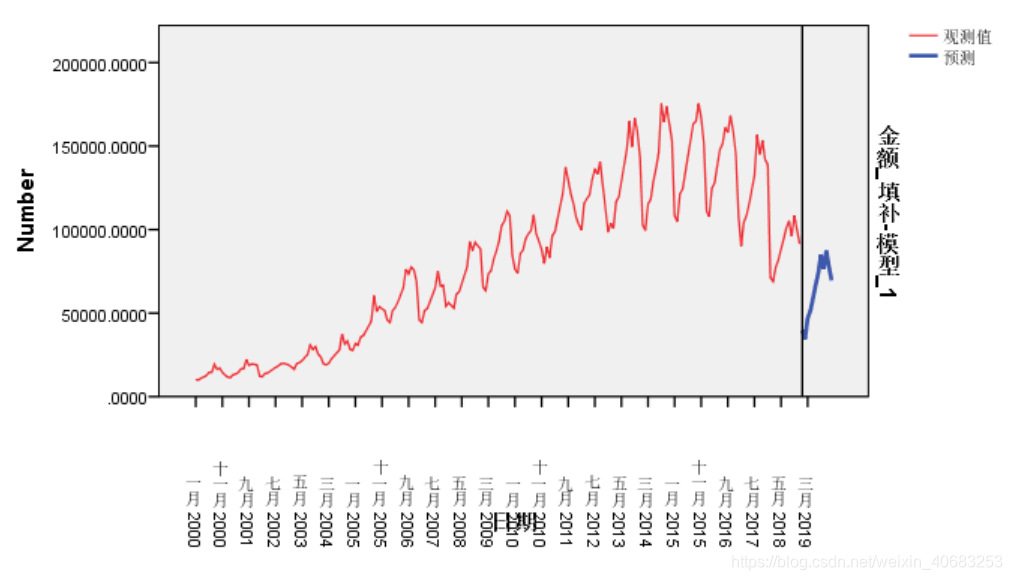
第七步：预测

【分析】--【预测】--【创建模型】

输出（图表中蓝色线为预测值），同时数据表中也会自动保存具体的预测值：

使用的时候导出就好，（左上角：【文件】--【另存为】)