本文为 scikit-learn机器学习（第2版）学习笔记

1. 多元线性回归

模型 $y=\alpha +{\beta }_1{x}_1+{\beta }_2{x}_2+...+{\beta }_n{x}_n$

写成向量形式：$Y=X\beta \to \beta =(X^{T}X{)}^{-1}{X}^{T}Y$

还是披萨价格预测的背景：

• 特征：披萨直径、配料数量，预测目标：披萨价格
• 参数包含：一个截距项、两个特征的系数

from numpy.linalg import inv
from numpy import dot, transpose
X = [[1, 6, 2], [1, 8, 1], [1, 10, 0], [1, 14, 2], [1, 18, 0]]
y = [[7], [9], [13], [17.5], [18]]
print(dot(inv(dot(transpose(X),X)), dot(transpose(X),y)))from numpy.linalg import lstsq
# help(lstsq)
print(lstsq(X,y))

[[1.1875    ][1.01041667][0.39583333]](array([[1.1875    ],[1.01041667],[0.39583333]]), array([8.22916667]), 3, array([26.97402951,  2.46027806,  0.59056212]))系数， 			残差，     			秩， 奇异值

• sklearn 线性回归

from sklearn.linear_model import LinearRegression
X = [[6, 2], [8, 1], [10, 0], [14, 2], [18, 0]]
y = [[7], [9], [13], [17.5], [18]]model = LinearRegression()
model.fit(X, y)X_test = [[8, 2], [9, 0], [11, 2], [16, 2], [12, 0]]
y_test = [[11], [8.5], [15], [18], [11]]
predictions = model.predict(X_test)for i, pred in enumerate(predictions):print("预测值：%s, 实际值：%s" %(pred, y_test[i]))
print(model.score(X_test,y_test))

预测值：[10.0625], 实际值：[11]
预测值：[10.28125], 实际值：[8.5]
预测值：[13.09375], 实际值：[15]
预测值：[18.14583333], 实际值：[18]
预测值：[13.3125], 实际值：[11]
0.7701677731318468 # r_squared

2. 多项式回归

披萨的价格跟直径之间可能不是线性的关系

二阶多项式模型：$y=\alpha +{\beta }_{1}x+{\beta }_2{x}^2$

import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.preprocessing import PolynomialFeaturesX_train = [[6], [8], [10], [14], [18]] # 直径
y_train = [[7], [9], [13], [17.5], [18]]
X_test = [[6], [8], [11], [16]] # 价格
y_test = [[8], [12], [15], [18]]
regressor = LinearRegression()
regressor.fit(X_train, y_train)
xx = np.linspace(0, 26, 100)
yy = regressor.predict(xx.reshape(xx.shape[0], 1))
plt.plot(xx, yy, c='g',linestyle='-')# 2次项特征转换器
quadratic_featurizer = PolynomialFeatures(degree=2)
X_train_quadratic = quadratic_featurizer.fit_transform(X_train)
X_test_quadratic = quadratic_featurizer.transform(X_test)
print("原特征\n",X_train)
print("二次项特征\n",X_train_quadratic)regressor_quadratic = LinearRegression()
regressor_quadratic.fit(X_train_quadratic, y_train)
xx_quadratic = quadratic_featurizer.transform(xx.reshape(xx.shape[0], 1))
plt.plot(xx, regressor_quadratic.predict(xx_quadratic), c='r', linestyle='--')
plt.rcParams['font.sans-serif'] = 'SimHei'  # 消除中文乱码
plt.title('披萨价格 VS 直径')
plt.xlabel('直径')
plt.ylabel('价格')
plt.axis([0, 25, 0, 25])
plt.grid(True)
plt.scatter(X_train, y_train)
plt.show()print('简单线性回归 r-squared值', regressor.score(X_test, y_test))
print('二次多项式回归 r-squared值', regressor_quadratic.score(X_test_quadratic, y_test))

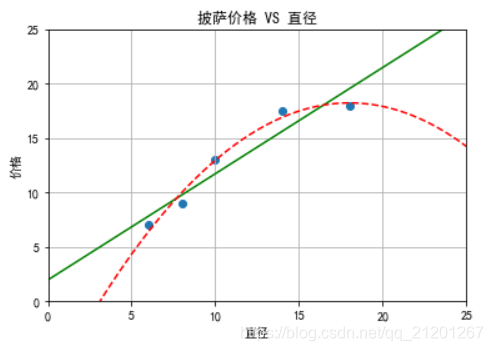
原特征[[6], [8], [10], [14], [18]]
二次项特征[[  1.   6.  36.][  1.   8.  64.][  1.  10. 100.][  1.  14. 196.][  1.  18. 324.]]简单线性回归 r-squared值 0.809726797707665
二次多项式回归 r-squared值 0.8675443656345054 # 决定系数更大

当改为 3 阶拟合时，多项式回归 r-squared值 0.8356924156037133
当改为 4 阶拟合时，多项式回归 r-squared值 0.8095880795746723
当改为 9 阶拟合时，多项式回归 r-squared值 -0.09435666704315328

为9阶时，模型完全拟合了训练数据，却不能够很好地对 test 集做出好的预测，称之过拟合

3. 正则化

正则化，预防过拟合

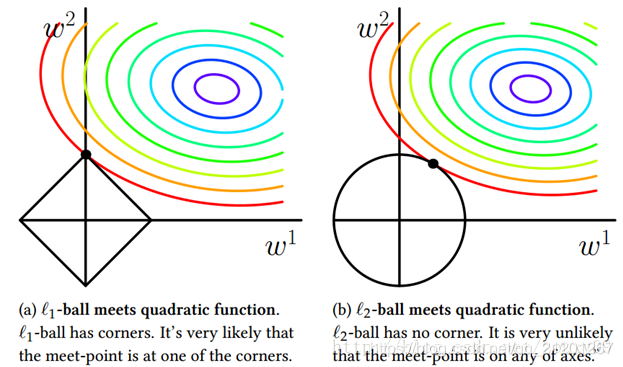
L1 正则可以实现特征的稀疏（趋于产生少量特征，其他为0）
L2 正则可以防止过拟合，提升模型的泛化能力（选择更多的特征，特征更一致的向0收缩，但不为0）

4. 线性回归应用举例（酒质量预测）

酒的质量预测（0-10的离散值，本例子假定是连续的，做回归预测）
特征：11种物理化学性质

4.1 数据预览

# 酒质量预测
import pandas as pd
data = pd.read_csv("winequality-red.csv",sep=';')
data.describe()

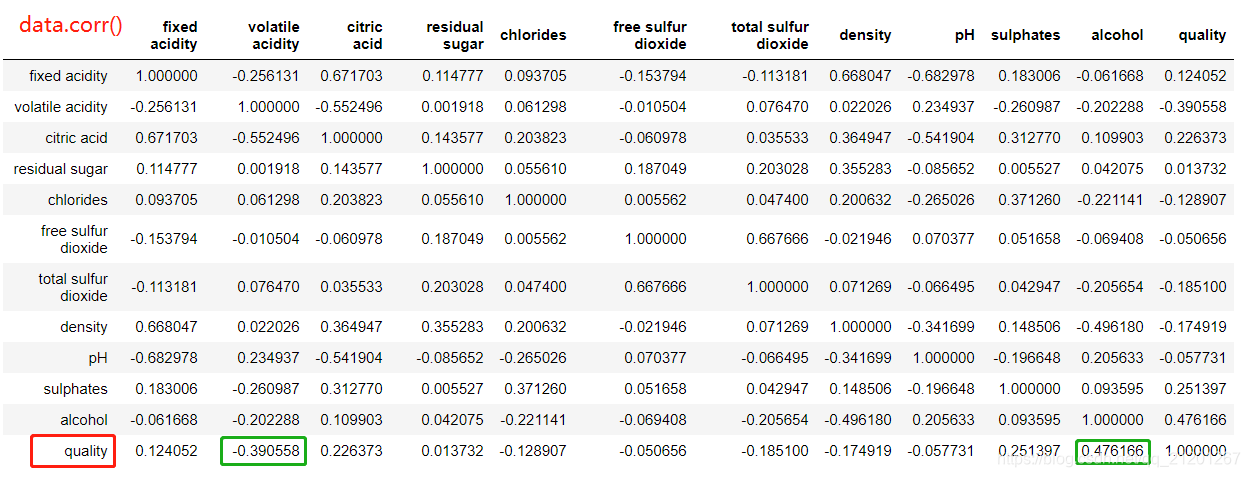
相关系数矩阵显示，酒的质量 跟 酒精含量 呈较强的正相关，跟 柠檬酸 呈较强的负相关性

4.2 模型验证

from sklearn.linear_model import LinearRegression
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_splitX = data[list(data.columns)[:-1]]
y = data['quality']
X_train,X_test,y_train,y_test = train_test_split(X,y)regressor = LinearRegression()
regressor.fit(X_train,y_train)
y_pred = regressor.predict(X_test)
print("决定系数：", regressor.score(X_test,y_test))
# 决定系数： 0.3602241149540347

• 5 折交叉验证

from sklearn.model_selection import cross_val_score
scores = cross_val_score(regressor, X, y, cv=5)
scores.mean() # 0.2900416288421962
scores # array([0.13200871, 0.31858135, 0.34955348, 0.369145  , 0.2809196 ])

5. 梯度下降法

一种有效估计 模型最佳参数 的方法

朝着代价函数下降最快的梯度迈出步伐（步长，也叫学习率）

• 学习率太小，收敛时间边长
• 学习率太大，会在局部极小值附近震荡，不收敛

根据每次训练迭代，使用的训练实例数量：

• 批次梯度下降：每次训练，使用全部实例来更新模型参数，时间长，结果确定
• 随机梯度下降：每次训练，随机选取一个实例，时间短，每次结果不确定，接近极小值

sklearn 的 SGDRegressor 是随机梯度下降的一种实现

import numpy as np
from sklearn.datasets import load_boston
from sklearn.linear_model import SGDRegressor
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_splitdata = load_boston()
X_train, X_test, y_train, y_test = train_test_split(data.data, data.target)X_scaler = StandardScaler()
y_scaler = StandardScaler()
X_train = X_scaler.fit_transform(X_train)
y_train = y_scaler.fit_transform(y_train.reshape(-1, 1))
X_test = X_scaler.transform(X_test)
y_test = y_scaler.transform(y_test.reshape(-1, 1))regressor = SGDRegressor(loss='squared_loss')
scores = cross_val_score(regressor, X_train, y_train, cv=5)print('Cross validation r-squared scores: %s' % scores)
print('Average cross validation r-squared score: %s' % np.mean(scores))regressor.fit(X_train, y_train)
print('Test set r-squared score %s' % regressor.score(X_test, y_test))

Cross validation r-squared scores: [0.57365322 0.73833251 0.69391029 0.67979254 0.73491949]
Average cross validation r-squared score: 0.6841216111623614
Test set r-squared score 0.7716363798764403

help(SGDRegressor)

class SGDRegressor(BaseSGDRegressor)|  SGDRegressor(loss='squared_loss', penalty='l2', alpha=0.0001, l1_ratio=0.15, fit_intercept=True, max_iter=1000, tol=0.001, shuffle=True, verbose=0, epsilon=0.1, random_state=None,learning_rate='invscaling', eta0=0.01, power_t=0.25, early_stopping=False, validation_fraction=0.1, n_iter_no_change=5, warm_start=False, average=False)|  |  Linear model fitted by minimizing a regularized empirical loss with SGD|  |  SGD stands for Stochastic Gradient Descent: the gradient of the loss is|  estimated each sample at a time and the model is updated along the way with|  a decreasing strength schedule (aka learning rate).|  |  The regularizer is a penalty added to the loss function that shrinks model|  parameters towards the zero vector using either the squared euclidean norm|  L2 or the absolute norm L1 or a combination of both (Elastic Net). If the|  parameter update crosses the 0.0 value because of the regularizer, the|  update is truncated to 0.0 to allow for learning sparse models and achieve|  online feature selection.