本文是Koala带你进入GIS世界的开篇,Koala打算用简单通俗的语言为大家介绍地图投影,帮助GISer理解地图投影的概念。作为进入GIS世界多年的老鸟,Koala也是在不断的实战中才真正理解和掌握地图投影的奥秘。
我们生活的地球长啥模样?
很久很久以前(相当白话的开场),人类就开始琢磨地球是如何存在的。《十万个为什么》告诉我们,古印度人认为地球是被四只站立在乌龟背上的大象支撑着的,而乌龟又趴在首尾相连的眼镜蛇上面(这乌龟的腿该多细啊……)。古希腊的哲学家毕达哥拉斯率先提出地球是球形的,不过这哥们得出这个结论的依据竟然是他认为圆球是所有几何形体中最完美的。又过了几年,亚里士多德根据月食时月面出现的地影是圆形的,给出了地球是球形的结论,显然这个比较靠谱,果然是大贤!直到1622年葡萄牙驴友麦哲伦不花自己的钱,坐着邮轮环游世界,证明地球确实是圆形的。这告诉我们把兴趣和事业结合在一起,是多么幸福的一件事。
![earth shape_thumb[2] earth shape_thumb[2]](https://images.cnblogs.com/cnblogs_com/laoyu/201206/201206032322208082.png)
工业革命以后,经过天文大地测量、地球重力测量、卫星大地测量等精密测量后,人们发现:地球并不是一个正球体,而是一个极半径略短、赤道半径略长,北极略突出、南极略扁平,近于梨形的椭球体。
Discovery中的地球是那么梦幻,那么婀娜。
![earth_thumb[1] earth_thumb[1]](https://images.cnblogs.com/cnblogs_com/laoyu/201206/201206032322231622.png)
真实世界的地球却长得非常不光滑,坑坑洼洼到令人发指,珠穆朗玛与马里亚纳海沟之间的高差竟达20km。
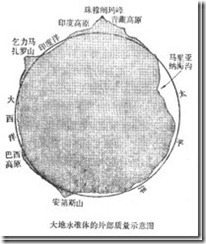
为了能够精确描述地球表面形状,人们试图寻找一种与地球自然表面非常接近的规则曲面,来代替地球不规则的自然表面,这就是大地水准面。
大地水准面
假想将静止的平均海水面延伸到大陆内部,形成一个连续不断的,与地球比较接近的形体,其表面称为大地水准面。有了大地水准面以后,我们就可以使用仪器来测量海拔高程:某点到大地水准面的高度。

地球的数学表面(看到数学二字,是不是有客官已经开始面部抽搐了?)
为了测量成果的计算和制图工作的需要,科学家选用一个同大地体相近的,可以用数学方法来表达的旋转椭球体来代替地球。这个旋转椭球被称为地球椭球体——地球的数学表面。
地球椭球体三要素:长轴a (赤道半径)短轴b (极半径)椭球扁率:f=(a-b)/a

对地球形状 a,b,f 测定后,还必须确定大地水准面与椭球体面的相对关系。即确定与局部地区大地水准面符合最好的一个地球椭球体 —— 参考椭球体,这项工作就是参考椭球体定位。
通过数学方法将地球椭球体摆到与大地水准面最贴近的位置上,并求出两者各点垂直的偏差。
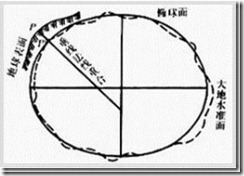
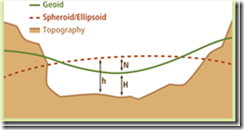
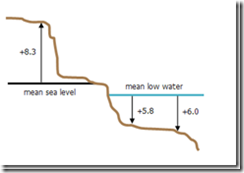
h = H + N,大地高:H,正常高:h,异常值:N





)

)


)
)
)



)


