测试题：参考博文

笔记：02.改善深层神经网络：超参数调试、正则化以及优化 W1.深度学习的实践层面

作业1：初始化

好的初始化：

• 加快梯度下降的收敛速度
• 增加梯度下降收敛到较低的训练（和泛化）误差的几率

导入数据

import numpy as np
import matplotlib.pyplot as plt
import sklearn
import sklearn.datasets
from init_utils import sigmoid, relu, compute_loss, forward_propagation, backward_propagation
from init_utils import update_parameters, predict, load_dataset, plot_decision_boundary, predict_dec%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'# load image dataset: blue/red dots in circles
train_X, train_Y, test_X, test_Y = load_dataset()

我们的任务是：将两类点分类

1. 神经网络模型

用一个已经实现好了的 3层神经网络

def model(X, Y, learning_rate = 0.01, num_iterations = 15000, print_cost = True, initialization = "he"):"""Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.Arguments:X -- input data, of shape (2, number of examples)Y -- true "label" vector (containing 0 for red dots; 1 for blue dots), of shape (1, number of examples)learning_rate -- learning rate for gradient descent num_iterations -- number of iterations to run gradient descentprint_cost -- if True, print the cost every 1000 iterationsinitialization -- flag to choose which initialization to use ("zeros","random" or "he")Returns:parameters -- parameters learnt by the model"""grads = {}costs = [] # to keep track of the lossm = X.shape[1] # number of exampleslayers_dims = [X.shape[0], 10, 5, 1]# Initialize parameters dictionary.if initialization == "zeros":parameters = initialize_parameters_zeros(layers_dims)elif initialization == "random":parameters = initialize_parameters_random(layers_dims)elif initialization == "he":parameters = initialize_parameters_he(layers_dims)# Loop (gradient descent)for i in range(0, num_iterations):# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.a3, cache = forward_propagation(X, parameters)# Losscost = compute_loss(a3, Y)# Backward propagation.grads = backward_propagation(X, Y, cache)# Update parameters.parameters = update_parameters(parameters, grads, learning_rate)# Print the loss every 1000 iterationsif print_cost and i % 1000 == 0:print("Cost after iteration {}: {}".format(i, cost))costs.append(cost)# plot the lossplt.plot(costs)plt.ylabel('cost')plt.xlabel('iterations (per hundreds)')plt.title("Learning rate =" + str(learning_rate))plt.show()return parameters

2. 使用 0 初始化

# GRADED FUNCTION: initialize_parameters_zeros def initialize_parameters_zeros(layers_dims):"""Arguments:layer_dims -- python array (list) containing the size of each layer.Returns:parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])b1 -- bias vector of shape (layers_dims[1], 1)...WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])bL -- bias vector of shape (layers_dims[L], 1)"""parameters = {}L = len(layers_dims)            # number of layers in the networkfor l in range(1, L):### START CODE HERE ### (≈ 2 lines of code)parameters['W' + str(l)] = np.zeros((layers_dims[l], layers_dims[l-1]))parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))### END CODE HERE ###return parameters

运行以下代码训练：

parameters = model(train_X, train_Y, initialization = "zeros")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

结果：

Cost after iteration 0: 0.6931471805599453
Cost after iteration 1000: 0.6931471805599453
Cost after iteration 2000: 0.6931471805599453
Cost after iteration 3000: 0.6931471805599453
Cost after iteration 4000: 0.6931471805599453
Cost after iteration 5000: 0.6931471805599453
Cost after iteration 6000: 0.6931471805599453
Cost after iteration 7000: 0.6931471805599453
Cost after iteration 8000: 0.6931471805599453
Cost after iteration 9000: 0.6931471805599453
Cost after iteration 10000: 0.6931471805599455
Cost after iteration 11000: 0.6931471805599453
Cost after iteration 12000: 0.6931471805599453
Cost after iteration 13000: 0.6931471805599453
Cost after iteration 14000: 0.6931471805599453

On the train set:
Accuracy: 0.5
On the test set:
Accuracy: 0.5

• 效果很差，代价函数几乎没有下降

print ("predictions_train = " + str(predictions_train))
print ("predictions_test = " + str(predictions_test))

预测全部都是 0

predictions_train = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0]]
predictions_test = [[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]]

plt.title("Model with Zeros initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

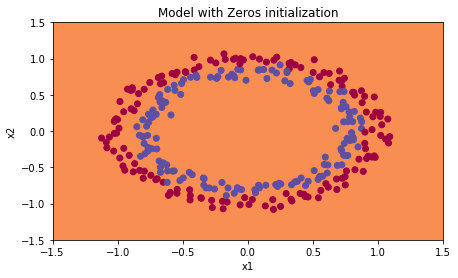
结论：

• 神经网络中，不要把参数初始化为0，否则模型不能打破这种状态，一直学习同样的东西。
• 可以将权重随机初始化，偏置初始化为0

3. 随机初始化

• np.random.randn(layers_dims[l], layers_dims[l-1])*10，* 10 使用很大的随机数初始化权重

# GRADED FUNCTION: initialize_parameters_randomdef initialize_parameters_random(layers_dims):"""Arguments:layer_dims -- python array (list) containing the size of each layer.Returns:parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])b1 -- bias vector of shape (layers_dims[1], 1)...WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])bL -- bias vector of shape (layers_dims[L], 1)"""np.random.seed(3)               # This seed makes sure your "random" numbers will be the as oursparameters = {}L = len(layers_dims)            # integer representing the number of layersfor l in range(1, L):### START CODE HERE ### (≈ 2 lines of code)parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*10parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))### END CODE HERE ###return parameters

运行以下代码训练：

parameters = model(train_X, train_Y, initialization = "random")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

结果：

Cost after iteration 0: inf
Cost after iteration 1000: 0.6239567039908781
Cost after iteration 2000: 0.5978043872838292
Cost after iteration 3000: 0.563595830364618
Cost after iteration 4000: 0.5500816882570866
Cost after iteration 5000: 0.5443417928662615
Cost after iteration 6000: 0.5373553777823036
Cost after iteration 7000: 0.4700141958024487
Cost after iteration 8000: 0.3976617665785177
Cost after iteration 9000: 0.39344405717719166
Cost after iteration 10000: 0.39201765232720626
Cost after iteration 11000: 0.38910685278803786
Cost after iteration 12000: 0.38612995897697244
Cost after iteration 13000: 0.3849735792031832
Cost after iteration 14000: 0.38275100578285265

On the train set:
Accuracy: 0.83
On the test set:
Accuracy: 0.86

决策边界

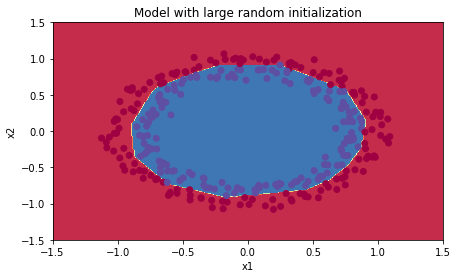
plt.title("Model with large random initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

将* 10 改为 * 1：

Cost after iteration 0: 1.9698193182646349
Cost after iteration 1000: 0.6894749458317239
Cost after iteration 2000: 0.675058063210226
Cost after iteration 3000: 0.6469210868251528
Cost after iteration 4000: 0.5398790761260324
Cost after iteration 5000: 0.4062642269764849
Cost after iteration 6000: 0.29844708868759456
Cost after iteration 7000: 0.22183734662094845
Cost after iteration 8000: 0.16926424179038072
Cost after iteration 9000: 0.1341330896982709
Cost after iteration 10000: 0.10873865543082417
Cost after iteration 11000: 0.09169443068126971
Cost after iteration 12000: 0.07991173603998084
Cost after iteration 13000: 0.07083949901112582
Cost after iteration 14000: 0.06370209022580517

On the train set:
Accuracy: 0.9966666666666667
On the test set:
Accuracy: 0.96

将* 10 改为 * 0.1：

Cost after iteration 0: 0.6933234320329613
Cost after iteration 1000: 0.6932871248121155
Cost after iteration 2000: 0.6932558729405607
Cost after iteration 3000: 0.6932263488895136
Cost after iteration 4000: 0.6931989886931527
Cost after iteration 5000: 0.6931076575962486
Cost after iteration 6000: 0.6930655602542224
Cost after iteration 7000: 0.6930202936477311
Cost after iteration 8000: 0.6929722630100763
Cost after iteration 9000: 0.6929185743666864
Cost after iteration 10000: 0.6928576152283971
Cost after iteration 11000: 0.6927869030178897
Cost after iteration 12000: 0.6927029749978133
Cost after iteration 13000: 0.6926024266332704
Cost after iteration 14000: 0.6924787835871681

On the train set:
Accuracy: 0.6
On the test set:
Accuracy: 0.57

• 使用合适的初始化权重非常重要！！！
• 不好的初始化会造成梯度消失/爆炸，降低了学习速度

4. He 初始化

是以一个人的名字命名的。

• 如果使用ReLu激活函数（最常用），$\ast np.sqrt(\frac{2}{n^{[l-1]}})$
• 如果使用tanh激活函数，$\sqrt{\frac{1}{n^{[l-1]}}}$，或者 $\sqrt{\frac{2}{n^{[l-1]}+n^{[l]}}}$

# GRADED FUNCTION: initialize_parameters_hedef initialize_parameters_he(layers_dims):"""Arguments:layer_dims -- python array (list) containing the size of each layer.Returns:parameters -- python dictionary containing your parameters "W1", "b1", ..., "WL", "bL":W1 -- weight matrix of shape (layers_dims[1], layers_dims[0])b1 -- bias vector of shape (layers_dims[1], 1)...WL -- weight matrix of shape (layers_dims[L], layers_dims[L-1])bL -- bias vector of shape (layers_dims[L], 1)"""np.random.seed(3)parameters = {}L = len(layers_dims) - 1 # integer representing the number of layersfor l in range(1, L + 1):### START CODE HERE ### (≈ 2 lines of code)parameters['W' + str(l)] = np.random.randn(layers_dims[l], layers_dims[l-1])*np.sqrt(2/layers_dims[l-1])parameters['b' + str(l)] = np.zeros((layers_dims[l], 1))### END CODE HERE ###return parameters

parameters = model(train_X, train_Y, initialization = "he")
print ("On the train set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

Cost after iteration 0: 0.8830537463419761
Cost after iteration 1000: 0.6879825919728063
Cost after iteration 2000: 0.6751286264523371
Cost after iteration 3000: 0.6526117768893807
Cost after iteration 4000: 0.6082958970572938
Cost after iteration 5000: 0.5304944491717495
Cost after iteration 6000: 0.4138645817071794
Cost after iteration 7000: 0.3117803464844441
Cost after iteration 8000: 0.23696215330322562
Cost after iteration 9000: 0.18597287209206836
Cost after iteration 10000: 0.15015556280371817
Cost after iteration 11000: 0.12325079292273552
Cost after iteration 12000: 0.09917746546525932
Cost after iteration 13000: 0.08457055954024274
Cost after iteration 14000: 0.07357895962677362

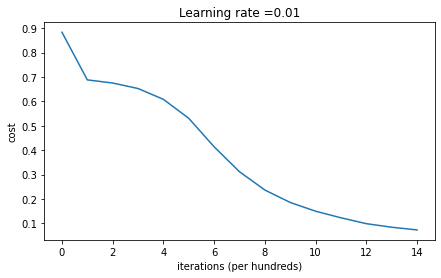
On the train set:
Accuracy: 0.9933333333333333
On the test set:
Accuracy: 0.96

plt.title("Model with He initialization")
axes = plt.gca()
axes.set_xlim([-1.5,1.5])
axes.set_ylim([-1.5,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

模型	训练准确率	问题
3-layer NN with zeros initialization	50%	fails to break symmetry
3-layer NN with large random initialization	83%	too large weights
3-layer NN with He initialization	99%	recommended method

作业2：正则化

过拟合是个严重的问题，它表现为在训练集上表现的很好，但是泛化性能较差

# import packages
import numpy as np
import matplotlib.pyplot as plt
from reg_utils import sigmoid, relu, plot_decision_boundary, initialize_parameters, load_2D_dataset, predict_dec
from reg_utils import compute_cost, predict, forward_propagation, backward_propagation, update_parameters
import sklearn
import sklearn.datasets
import scipy.io
from testCases import *%matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

问题引入：

法国足球守门员发球，把球踢到什么位置，他的队友可以用头顶球。

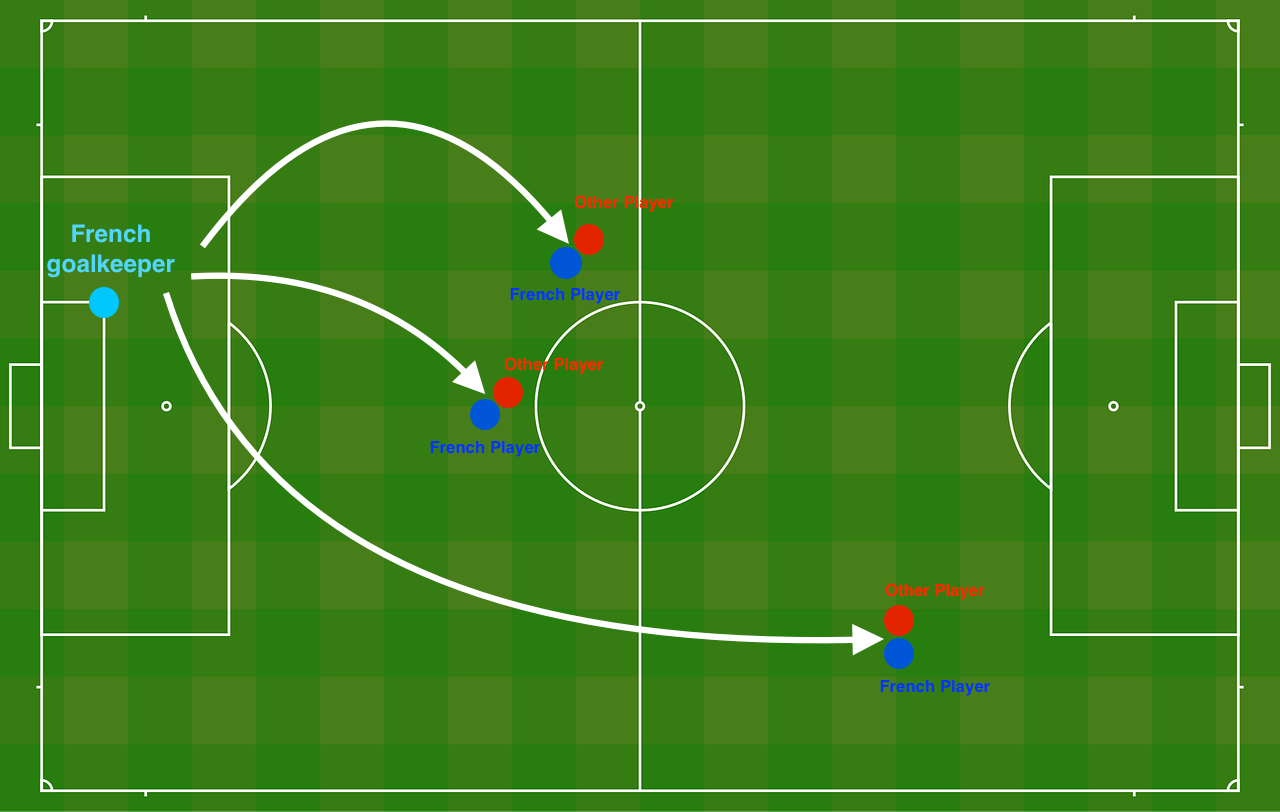
train_X, train_Y, test_X, test_Y = load_2D_dataset()

法国守门员从左侧发球，蓝色是自己队友顶球位置，红色是对方顶球位置

肉眼看，好像可以用一条45°左右的斜线分开

1. 无正则化模型

def model(X, Y, learning_rate = 0.3, num_iterations = 30000, print_cost = True, lambd = 0, keep_prob = 1):"""Implements a three-layer neural network: LINEAR->RELU->LINEAR->RELU->LINEAR->SIGMOID.Arguments:X -- input data, of shape (input size, number of examples)Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (output size, number of examples)learning_rate -- learning rate of the optimizationnum_iterations -- number of iterations of the optimization loopprint_cost -- If True, print the cost every 10000 iterationslambd -- regularization hyperparameter, scalarkeep_prob - probability of keeping a neuron active during drop-out, scalar.Returns:parameters -- parameters learned by the model. They can then be used to predict."""grads = {}costs = []                            # to keep track of the costm = X.shape[1]                        # number of exampleslayers_dims = [X.shape[0], 20, 3, 1]# Initialize parameters dictionary.parameters = initialize_parameters(layers_dims)# Loop (gradient descent)for i in range(0, num_iterations):# Forward propagation: LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOID.if keep_prob == 1:a3, cache = forward_propagation(X, parameters)elif keep_prob < 1:a3, cache = forward_propagation_with_dropout(X, parameters, keep_prob)# Cost functionif lambd == 0:cost = compute_cost(a3, Y)else:cost = compute_cost_with_regularization(a3, Y, parameters, lambd)# Backward propagation.assert(lambd==0 or keep_prob==1)    # it is possible to use both L2 regularization and dropout, # but this assignment will only explore one at a timeif lambd == 0 and keep_prob == 1:grads = backward_propagation(X, Y, cache)elif lambd != 0:grads = backward_propagation_with_regularization(X, Y, cache, lambd)elif keep_prob < 1:grads = backward_propagation_with_dropout(X, Y, cache, keep_prob)# Update parameters.parameters = update_parameters(parameters, grads, learning_rate)# Print the loss every 10000 iterationsif print_cost and i % 10000 == 0:print("Cost after iteration {}: {}".format(i, cost))if print_cost and i % 1000 == 0:costs.append(cost)# plot the costplt.plot(costs)plt.ylabel('cost')plt.xlabel('iterations (x1,000)')plt.title("Learning rate =" + str(learning_rate))plt.show()return parameters

parameters = model(train_X, train_Y)
print ("On the training set:")
predictions_train = predict(train_X, train_Y, parameters)
print ("On the test set:")
predictions_test = predict(test_X, test_Y, parameters)

• 无正则化 训练过程

Cost after iteration 0: 0.6557412523481002
Cost after iteration 10000: 0.16329987525724213
Cost after iteration 20000: 0.13851642423245572

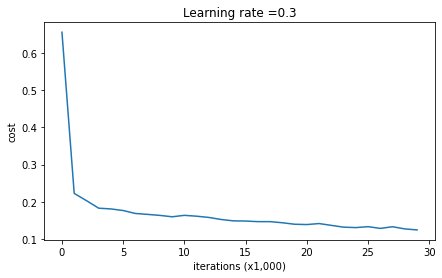
On the training set:
Accuracy: 0.9478672985781991
On the test set:
Accuracy: 0.915

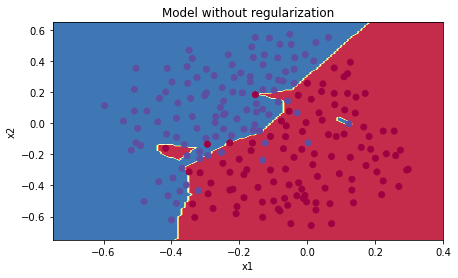
• 没有正则化的模型过拟合了，它拟合了一些噪声点

2. L2 正则化

• 注意在损失函数里加入正则化项

无正则项的损失函数：
$$J=-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \left(a^{[L](i)}\right)+(1-y^{(i)})\log \left(1-a^{[L](i)}\right))$$
加入正则化项的损失函数：
$$J_{regularized}=\underset{\text{cross-entropy cost}}{\underbrace{-\frac{1}{m}\sum _{i=1}^m(y^{(i)}\log \left(a^{[L](i)}\right)+(1-y^{(i)})\log \left(1-a^{[L](i)}\right))}}+\underset{\text{L2 regularization cost}}{\underbrace{\frac{1}{m}\frac{\lambda }{2}\sum _l\sum _k\sum _j{W}_{k,j}^{[l]2}}}$$

>>> w1 = np.array([[1,2],[2,3]])		  
>>> w1	  
array([[1, 2],[2, 3]])
>>> np.sum(np.square(w1))		  
18

# GRADED FUNCTION: compute_cost_with_regularizationdef compute_cost_with_regularization(A3, Y, parameters, lambd):"""Implement the cost function with L2 regularization. See formula (2) above.Arguments:A3 -- post-activation, output of forward propagation, of shape (output size, number of examples)Y -- "true" labels vector, of shape (output size, number of examples)parameters -- python dictionary containing parameters of the modelReturns:cost - value of the regularized loss function (formula (2))"""m = Y.shape[1]W1 = parameters["W1"]W2 = parameters["W2"]W3 = parameters["W3"]cross_entropy_cost = compute_cost(A3, Y) # This gives you the cross-entropy part of the cost### START CODE HERE ### (approx. 1 line)L2_regularization_cost = lambd/(2*m)*(np.sum(np.square(W1)) + np.sum(np.square(W2)) + np.sum(np.square(W3)))### END CODER HERE ###cost = cross_entropy_cost + L2_regularization_costreturn cost

• 反向传播，计算梯度时也要根据 新的损失函数
  dw 需要加入 $\frac{d}{dW}(\frac{1}{2}\frac{\lambda }{m}{W}^2)=\frac{\lambda }{m}W$ 项

# GRADED FUNCTION: backward_propagation_with_regularizationdef backward_propagation_with_regularization(X, Y, cache, lambd):"""Implements the backward propagation of our baseline model to which we added an L2 regularization.Arguments:X -- input dataset, of shape (input size, number of examples)Y -- "true" labels vector, of shape (output size, number of examples)cache -- cache output from forward_propagation()lambd -- regularization hyperparameter, scalarReturns:gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables"""m = X.shape[1](Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - Y### START CODE HERE ### (approx. 1 line)dW3 = 1./m * np.dot(dZ3, A2.T) + lambd/m*W3### END CODE HERE ###db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)dA2 = np.dot(W3.T, dZ3)dZ2 = np.multiply(dA2, np.int64(A2 > 0))### START CODE HERE ### (approx. 1 line)dW2 = 1./m * np.dot(dZ2, A1.T) + lambd/m*W2### END CODE HERE ###db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)dA1 = np.dot(W2.T, dZ2)dZ1 = np.multiply(dA1, np.int64(A1 > 0))### START CODE HERE ### (approx. 1 line)dW1 = 1./m * np.dot(dZ1, X.T) + lambd/m*W1### END CODE HERE ###db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

• 运行带 L2 正则化（ $\lambda$ = 0.7）的模型（使用上面两个函数计算损失、梯度）

Cost after iteration 0: 0.6974484493131264
Cost after iteration 10000: 0.26849188732822393
Cost after iteration 20000: 0.2680916337127301

On the train set:
Accuracy: 0.9383886255924171
On the test set:
Accuracy: 0.93

模型没有过拟合

L2 正则化使得 权重衰减，其基于假设： 小的权重 W 的模型更简单，所以模型会惩罚 大的 W，小的权重 使得输出变化比较平和，不会剧烈变化 形成复杂的边界（造成过拟合）

调整 $\lambda$ 做点对比：
$\lambda =0.3$

On the train set:
Accuracy: 0.919431279620853
On the test set:
Accuracy: 0.945

$\lambda =0.1$

On the train set:
Accuracy: 0.9383886255924171
On the test set:
Accuracy: 0.95

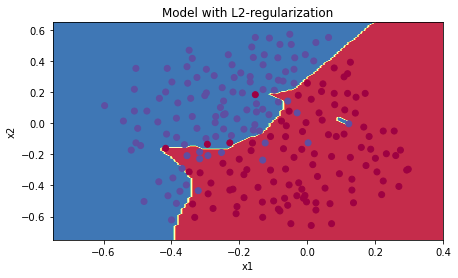
$\lambda =0.01$（正则化作用很弱）

On the train set:
Accuracy: 0.9289099526066351
On the test set:
Accuracy: 0.915

(有点过拟合)

$\lambda =1$

On the train set:
Accuracy: 0.9241706161137441
On the test set:
Accuracy: 0.93

$\lambda =5$

On the train set:
Accuracy: 0.919431279620853
On the test set:
Accuracy: 0.92

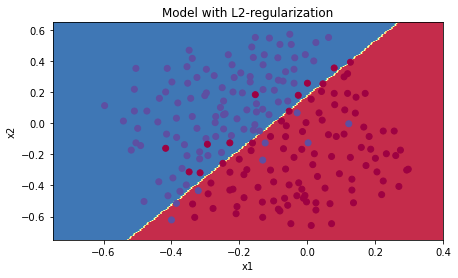
• $\lambda$ 太大，正则化太强，W 被压缩的很小，决策边界过度平滑（都直线了），造成高的偏差

3. DropOut 正则化

DropOut 正则化 在每次迭代的时候 随机关闭一些神经元
被关闭的神经元在当次迭代时，对前向和后向传播都没有贡献

drop-out背后的思想是，每次迭代时，使用部分神经元子集的不同模型，神经元对另一个特定神经元的激活变得不那么敏感，因为另一个神经元随时可能被关闭

3.1 带dropout的前向传播

对一个3层神经网络实施 dropout，只对第1，2层进行，不包括输入和输出层

• 用 np.random.rand() 建立与 $A^{[1]}$ 一样维度的 $D^{[1]}=[d^{[1](1)}{d}^{[1](2)}...d^{[1](m)}]$
• 以一定的概率，设置 $D^{[1]}$ 元素为0（概率 1-keep_prob）, 1（概率 keep_prob）X = (X < keep_prob)
• 关闭某些神经元，$A^{[1]}=A^{[1]}\ast D^{[1]}$
• $A^{[1]}/=\text{ keep-prob }$，此步确保损失函数的期望值与 没有dropout 时一样（inverted dropout）

# GRADED FUNCTION: forward_propagation_with_dropoutdef forward_propagation_with_dropout(X, parameters, keep_prob = 0.5):"""Implements the forward propagation: LINEAR -> RELU + DROPOUT -> LINEAR -> RELU + DROPOUT -> LINEAR -> SIGMOID.Arguments:X -- input dataset, of shape (2, number of examples)parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":W1 -- weight matrix of shape (20, 2)b1 -- bias vector of shape (20, 1)W2 -- weight matrix of shape (3, 20)b2 -- bias vector of shape (3, 1)W3 -- weight matrix of shape (1, 3)b3 -- bias vector of shape (1, 1)keep_prob - probability of keeping a neuron active during drop-out, scalarReturns:A3 -- last activation value, output of the forward propagation, of shape (1,1)cache -- tuple, information stored for computing the backward propagation"""np.random.seed(1)# retrieve parametersW1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDZ1 = np.dot(W1, X) + b1A1 = relu(Z1)### START CODE HERE ### (approx. 4 lines)         # Steps 1-4 below correspond to the Steps 1-4 described above. D1 = np.random.rand(A1.shape[0], A1.shape[1])   # Step 1: initialize matrix D1 = np.random.rand(..., ...)D1 = D1 < keep_prob                             # Step 2: convert entries of D1 to 0 or 1 (using keep_prob as the threshold)A1 = A1*D1                                      # Step 3: shut down some neurons of A1A1 = A1/keep_prob                               # Step 4: scale the value of neurons that haven't been shut down### END CODE HERE ###Z2 = np.dot(W2, A1) + b2A2 = relu(Z2)### START CODE HERE ### (approx. 4 lines)D2 = np.random.rand(A2.shape[0], A2.shape[1])  # Step 1: initialize matrix D2 = np.random.rand(..., ...)D2 = D2 < keep_prob                            # Step 2: convert entries of D2 to 0 or 1 (using keep_prob as the threshold)A2 = A2*D2                                    # Step 3: shut down some neurons of A2A2 = A2/keep_prob                             # Step 4: scale the value of neurons that haven't been shut down### END CODE HERE ###Z3 = np.dot(W3, A2) + b3A3 = sigmoid(Z3)cache = (Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3)return A3, cache

3.2 带dropout的后向传播

上面我们用 $D^{[1]},D^{[2]}$ 把神经元关闭了

• 使用相同的 $D^{[1]}$ 关闭 $dA1$
• $dA1/=\text{keep-prob}$，导数跟上面保持一致的系数

# GRADED FUNCTION: backward_propagation_with_dropoutdef backward_propagation_with_dropout(X, Y, cache, keep_prob):"""Implements the backward propagation of our baseline model to which we added dropout.Arguments:X -- input dataset, of shape (2, number of examples)Y -- "true" labels vector, of shape (output size, number of examples)cache -- cache output from forward_propagation_with_dropout()keep_prob - probability of keeping a neuron active during drop-out, scalarReturns:gradients -- A dictionary with the gradients with respect to each parameter, activation and pre-activation variables"""m = X.shape[1](Z1, D1, A1, W1, b1, Z2, D2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = 1./m * np.dot(dZ3, A2.T)db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)dA2 = np.dot(W3.T, dZ3)### START CODE HERE ### (≈ 2 lines of code)dA2 = dA2 * D2        # Step 1: Apply mask D2 to shut down the same neurons as during the forward propagationdA2 = dA2/keep_prob   # Step 2: Scale the value of neurons that haven't been shut down### END CODE HERE ###dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1./m * np.dot(dZ2, A1.T)db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)dA1 = np.dot(W2.T, dZ2)### START CODE HERE ### (≈ 2 lines of code)dA1 = dA1 * D1        # Step 1: Apply mask D1 to shut down the same neurons as during the forward propagationdA1 = dA1/keep_prob   # Step 2: Scale the value of neurons that haven't been shut down### END CODE HERE ###dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1./m * np.dot(dZ1, X.T)db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2,"dZ2": dZ2, "dW2": dW2, "db2": db2, "dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

3.3 运行模型

参数：keep_prob = 0.86，前后向传播 使用上面的两个函数

On the train set:
Accuracy: 0.9289099526066351
On the test set:
Accuracy: 0.95

模型没有过拟合，且 test 集上的准确率达到了 95%

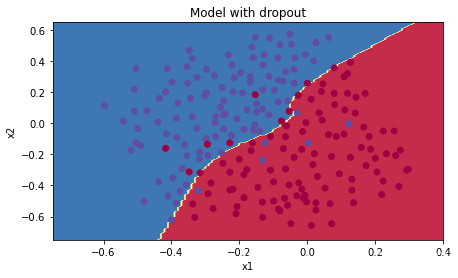
注意：

• 只能在训练的时候，使用dropout，测试的时候不要使用
• 前向、后向均应该使用

model	train accuracy	test accuracy
3-layer NN without regularization	95%	91.5%
3-layer NN with L2-regularization	94%	93%
3-layer NN with dropout	93%	95%

正则化限制了在训练集上的过拟合，训练准确率下降了，但是测试集准确率上升了，这是个好现象

作业3：梯度检验

梯度检验 确保 反向传播 是正确的，没有 bug

1. 1维梯度检验

$$\frac{\partial J}{\partial \theta }=\underset{\epsilon \to 0}{\lim }\frac{J(\theta +\epsilon )-J(\theta -\epsilon )}{2\epsilon }$$

• 计算理论梯度

# GRADED FUNCTION: forward_propagationdef forward_propagation(x, theta):"""Implement the linear forward propagation (compute J) presented in Figure 1 (J(theta) = theta * x)Arguments:x -- a real-valued inputtheta -- our parameter, a real number as wellReturns:J -- the value of function J, computed using the formula J(theta) = theta * x"""### START CODE HERE ### (approx. 1 line)J = theta * x### END CODE HERE ###return J

# GRADED FUNCTION: backward_propagationdef backward_propagation(x, theta):"""Computes the derivative of J with respect to theta (see Figure 1).Arguments:x -- a real-valued inputtheta -- our parameter, a real number as wellReturns:dtheta -- the gradient of the cost with respect to theta"""### START CODE HERE ### (approx. 1 line)dtheta = x### END CODE HERE ###return dtheta

• 计算近似梯度

1. ${\theta }^{+}=\theta +\epsilon$
2. ${\theta }^{-}=\theta -\epsilon$
3. $J^{+}=J({\theta }^{+})$
4. $J^{-}=J({\theta }^{-})$
5. $gradapprox=\frac{J^{+}-J^{-}}{2\epsilon }$

• 反向传播，计算理论梯度 grad
• 比较两者误差
  $$difference=\frac{\mid \mid grad-gradapprox\mid {\mid }_2}{\mid \mid grad\mid {\mid }_2+\mid \mid gradapprox\mid {\mid }_2}$$

np.linalg.norm(...)

• 检查上式是否足够小（10^-7）

# GRADED FUNCTION: gradient_checkdef gradient_check(x, theta, epsilon = 1e-7):"""Implement the backward propagation presented in Figure 1.Arguments:x -- a real-valued inputtheta -- our parameter, a real number as wellepsilon -- tiny shift to the input to compute approximated gradient with formula(1)Returns:difference -- difference (2) between the approximated gradient and the backward propagation gradient"""# Compute gradapprox using left side of formula (1). epsilon is small enough, you don't need to worry about the limit.### START CODE HERE ### (approx. 5 lines)thetaplus = theta + epsilon                     # Step 1thetaminus = theta - epsilon                    # Step 2J_plus = forward_propagation(x, thetaplus)      # Step 3J_minus = forward_propagation(x, thetaminus)    # Step 4gradapprox = (J_plus - J_minus)/(2*epsilon)    # Step 5### END CODE HERE #### Check if gradapprox is close enough to the output of backward_propagation()### START CODE HERE ### (approx. 1 line)grad = backward_propagation(x, theta)### END CODE HERE ###### START CODE HERE ### (approx. 1 line)numerator = np.linalg.norm(grad - gradapprox)  # Step 1'denominator = np.linalg.norm(grad) + np.linalg.norm(gradapprox) # Step 2'difference = numerator/denominator  # Step 3'### END CODE HERE ###if difference < 1e-7:print ("The gradient is correct!")else:print ("The gradient is wrong!")return difference

2. 多维梯度检验

def forward_propagation_n(X, Y, parameters):"""Implements the forward propagation (and computes the cost) presented in Figure 3.Arguments:X -- training set for m examplesY -- labels for m examples parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":W1 -- weight matrix of shape (5, 4)b1 -- bias vector of shape (5, 1)W2 -- weight matrix of shape (3, 5)b2 -- bias vector of shape (3, 1)W3 -- weight matrix of shape (1, 3)b3 -- bias vector of shape (1, 1)Returns:cost -- the cost function (logistic cost for one example)"""# retrieve parametersm = X.shape[1]W1 = parameters["W1"]b1 = parameters["b1"]W2 = parameters["W2"]b2 = parameters["b2"]W3 = parameters["W3"]b3 = parameters["b3"]# LINEAR -> RELU -> LINEAR -> RELU -> LINEAR -> SIGMOIDZ1 = np.dot(W1, X) + b1A1 = relu(Z1)Z2 = np.dot(W2, A1) + b2A2 = relu(Z2)Z3 = np.dot(W3, A2) + b3A3 = sigmoid(Z3)# Costlogprobs = np.multiply(-np.log(A3),Y) + np.multiply(-np.log(1 - A3), 1 - Y)cost = 1./m * np.sum(logprobs)cache = (Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3)return cost, cache

def backward_propagation_n(X, Y, cache):"""Implement the backward propagation presented in figure 2.Arguments:X -- input datapoint, of shape (input size, 1)Y -- true "label"cache -- cache output from forward_propagation_n()Returns:gradients -- A dictionary with the gradients of the cost with respect to each parameter, activation and pre-activation variables."""m = X.shape[1](Z1, A1, W1, b1, Z2, A2, W2, b2, Z3, A3, W3, b3) = cachedZ3 = A3 - YdW3 = 1./m * np.dot(dZ3, A2.T)db3 = 1./m * np.sum(dZ3, axis=1, keepdims = True)dA2 = np.dot(W3.T, dZ3)dZ2 = np.multiply(dA2, np.int64(A2 > 0))dW2 = 1./m * np.dot(dZ2, A1.T) * 2db2 = 1./m * np.sum(dZ2, axis=1, keepdims = True)dA1 = np.dot(W2.T, dZ2)dZ1 = np.multiply(dA1, np.int64(A1 > 0))dW1 = 1./m * np.dot(dZ1, X.T)db1 = 4./m * np.sum(dZ1, axis=1, keepdims = True)gradients = {"dZ3": dZ3, "dW3": dW3, "db3": db3,"dA2": dA2, "dZ2": dZ2, "dW2": dW2, "db2": db2,"dA1": dA1, "dZ1": dZ1, "dW1": dW1, "db1": db1}return gradients

# GRADED FUNCTION: gradient_check_ndef gradient_check_n(parameters, gradients, X, Y, epsilon = 1e-7):"""Checks if backward_propagation_n computes correctly the gradient of the cost output by forward_propagation_nArguments:parameters -- python dictionary containing your parameters "W1", "b1", "W2", "b2", "W3", "b3":grad -- output of backward_propagation_n, contains gradients of the cost with respect to the parameters. x -- input datapoint, of shape (input size, 1)y -- true "label"epsilon -- tiny shift to the input to compute approximated gradient with formula(1)Returns:difference -- difference (2) between the approximated gradient and the backward propagation gradient"""# Set-up variablesparameters_values, _ = dictionary_to_vector(parameters)grad = gradients_to_vector(gradients)num_parameters = parameters_values.shape[0]J_plus = np.zeros((num_parameters, 1))J_minus = np.zeros((num_parameters, 1))gradapprox = np.zeros((num_parameters, 1))# Compute gradapproxfor i in range(num_parameters):# Compute J_plus[i]. Inputs: "parameters_values, epsilon". Output = "J_plus[i]".# "_" is used because the function you have to outputs two parameters but we only care about the first one### START CODE HERE ### (approx. 3 lines)thetaplus = np.copy(parameters_values)                # Step 1thetaplus[i][0] = thetaplus[i][0] + epsilon          # Step 2J_plus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaplus)) # Step 3### END CODE HERE #### Compute J_minus[i]. Inputs: "parameters_values, epsilon". Output = "J_minus[i]".### START CODE HERE ### (approx. 3 lines)thetaminus = np.copy(parameters_values)               # Step 1thetaminus[i][0] = thetaminus[i][0] - epsilon        # Step 2        J_minus[i], _ = forward_propagation_n(X, Y, vector_to_dictionary(thetaminus)) # Step 3### END CODE HERE #### Compute gradapprox[i]### START CODE HERE ### (approx. 1 line)gradapprox[i] = (J_plus[i] - J_minus[i])/(2*epsilon)### END CODE HERE #### Compare gradapprox to backward propagation gradients by computing difference.### START CODE HERE ### (approx. 1 line)numerator = np.linalg.norm(gradapprox - grad)              # Step 1'denominator = np.linalg.norm(gradapprox)+np.linalg.norm(grad) # Step 2'difference = numerator/denominator                           # Step 3'### END CODE HERE ###if difference > 1e-7:print ("\033[93m" + "There is a mistake in the backward propagation! difference = " + str(difference) + "\033[0m")else:print ("\033[92m" + "Your backward propagation works perfectly fine! difference = " + str(difference) + "\033[0m")return difference

• 老师给的 backward_propagation_n 函数里面有错误，尝试去找到它。

X, Y, parameters = gradient_check_n_test_case()cost, cache = forward_propagation_n(X, Y, parameters)
gradients = backward_propagation_n(X, Y, cache)
difference = gradient_check_n(parameters, gradients, X, Y)

There is a mistake in the backward propagation! 
difference = 0.2850931567761624

• 寻找错误
  db1 改成：db1 = 1./m * np.sum(dZ1, axis=1, keepdims = True)
  dW2 改成：dW2 = 1./m * np.dot(dZ2, A1.T)

误差下来了，但略微超过 10^-7, 所以显示错误，应该问题不大

There is a mistake in the backward propagation! 
difference = 1.1890913023330276e-07

注意：

• 梯度检验非常慢，计算很耗时，所以我们训练时，不运行梯度检验，只运行几次检查梯度是否正确
• 梯度检验时，需要关掉 dropout

---

我的CSDN博客地址 https://michael.blog.csdn.net/

长按或扫码关注我的公众号（Michael阿明），一起加油、一起学习进步！