

随着互联网技术的高速发展,云计算已经成为各行各业的“水电煤”,成为“互联网+”的基础设施,而数据中心则是云服务背后的刚性保障。无论是传统的数据中心,还是云形态的数据中心,虚拟化技术都是提升其资源利用率、降低管理成本的重要方式。
据统计,早在2016年,AWS的服务器规模已经到达55万台,而虚拟机数量则超过了800万。随着虚拟机数量急剧增加,虚拟机的放置方案自然成为了决定数据中心资源利用率及其他需求的关键。
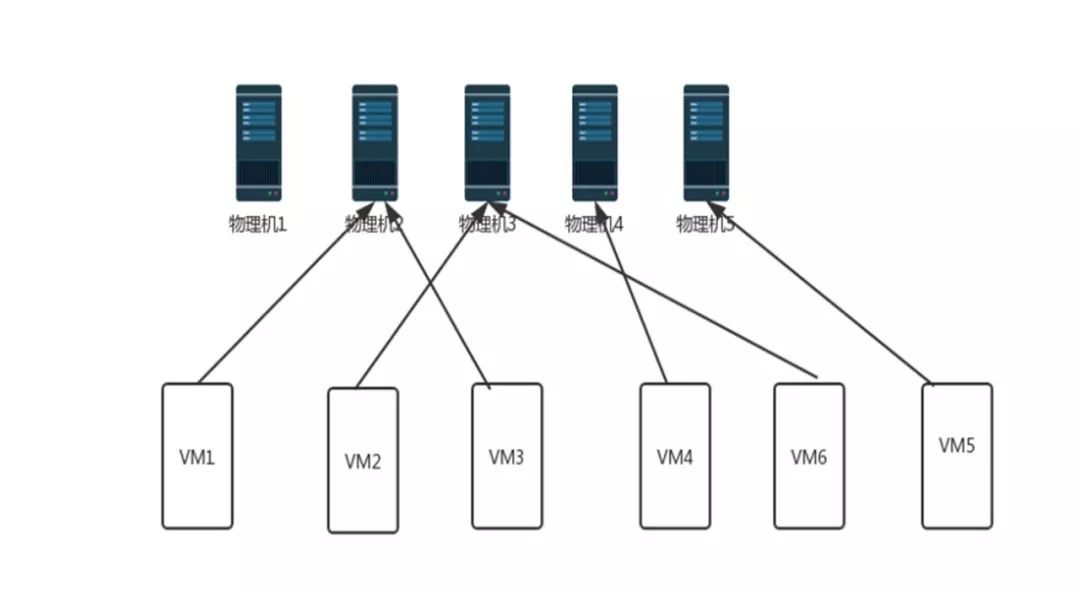
如果想提高数据中心的资源利用率,就需要采用合适的放置方案,使用最少的物理机便可以实现资源利用率的最优化,并起到节能的效果。而为了维持系统的高可用性,也需要选择合适的放置方案,使得不同服务器之间的资源使用率尽量均衡。
许多研究将虚拟机放置描述为“多维装箱”问题,装入的物品为虚拟机,其使用的资源为物品大小;而箱子则是物理机,箱子容量是物理机配置阈值,资源可包括CPU、内存、磁盘、网络带宽等,资源的种类数即为装箱问题的维度。
假设物理机数量为M,虚拟机数量为N,则理论上最多有M的N次方种部署方案,为NP-hard问题。在解决NP-hard问题的方法中,启发式算法如遗传算法、模拟退火算法等都有优秀的表现。在此我们介绍经典的遗传算法在解决该问题中的思路与具体落地方案。
遗传算法是一种全局优化搜索算法,以其简单通用、鲁棒性强、适于并行处理,以及高效和实用等显著特点,在各个领域得到了广泛应用。
遗传算法以一种群体中的所有个体为对象,并利用随机化技术对一个被编码的参数空间进行高效搜索。其中,选择、交叉和变异构成了遗传算法的遗传操作;编码、初始群体设定、适应度函数设计、遗传操作设计、控制参数设定五个要素组成了遗传算法的核心内容。那么,对于”虚拟机放置在物理机上”这个问题,怎么去理解遗传算法的五个要素呢?
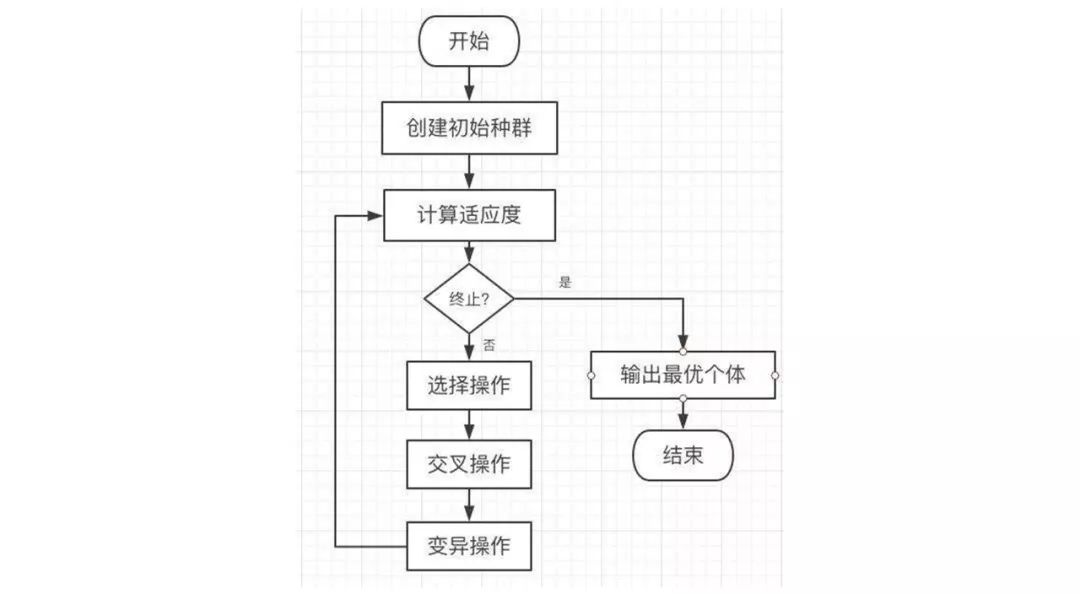
通过以下概念的释义,我们将现实世界中的虚拟机、物理机、虚拟机放置方案,评价当前方案的指标等问题,并映射到“遗传算法”过程中的专有名词,进而通过遗传算法进行求解:
染色体:一条染色体代表一种“当前虚拟机序列的放置方案”,也被称为种群中的个体;
评估染色体方式:不同的放置方案有着不同的适应值,而适应值决定了当前方案的优劣;通常采用物理机使用数量来评估染色体,同时考虑高可用限制、虚拟机数量限制等因素,这种面向多目标的问题可以使用“快速非支配排序”结合“局部拥挤距离”算法进行求解;
遗传组合行为(交叉、变异):改变染色体上的部分虚拟机的放置序列的行为;
种群:由多个染色体组成,代表当前进化次数下的染色体集合(多种放置方案的集合);
在将现实实体及问题映射到遗传算法的专有名词后,我们将演示如何把遗传算法的五个要素映射到现实问题中:
编码
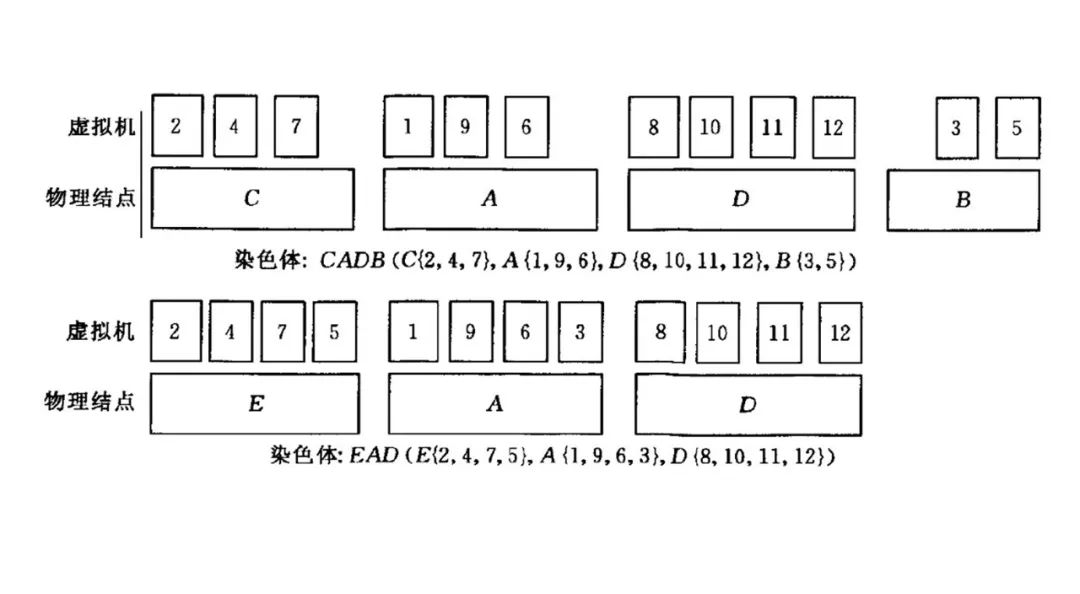
如上图所示,将每个“全量虚拟机序列在物理机序列上的放置方案”作为一条染色体,这是典型的进行“组编码”的方式,可以看到由于采用了不同物理机,两条染色体最终使用的物理机数量也是不同的。
初始群体设定
基于启发式的初始化群体方法可以降低算法优化过程的复杂度,但同时要保证群中染色体的多样性,这样是为了扩大搜索解空间,从而求解近似于全局最优解而非局部最优解;
在启发式算法中,第一个虚拟机放入第一个物理机,然后根据虚拟机序列顺序,依次放入其他虚拟机,直到第一个物理机资源不足。该过程可理解为:对于任意一台虚拟机,需先遍历当前已使用的物理机序列,直到被使用的物理机无法满足该资源需求。此时新开辟一台物理机为其使用——这是生成一条染色体的方式,同时为了保证种群的多样性,在每次生成新染色体时,我们需要随机打乱虚拟机序列的顺序,这种方法显然是简单而有效的。
适应度函数的设计
适应度是对当前种群中个体的评价方式,对于多目标优化问题一般可采用二代多目标优化算法NSGA2中的快速非支配排序进行个体等级划分,然后通过局部密度算法进行密度估计,确定每个个体的优先级。
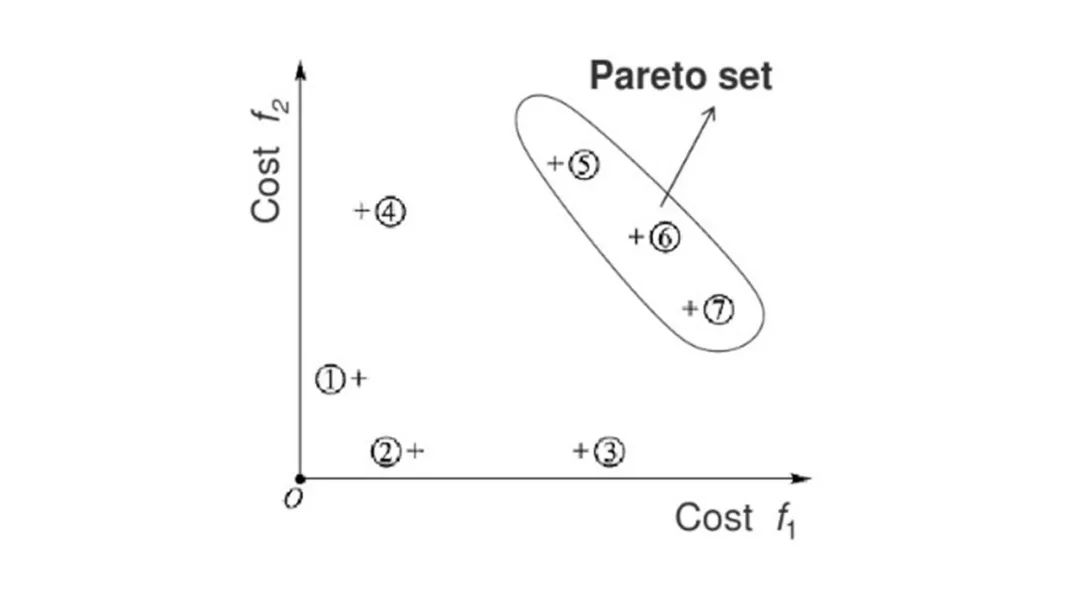
这个过程听起来很抽象,它的具体操作是怎样进行的呢? 如下图所示:若Costf1 和 Cost f2 分别表示个体在“使用物理机数量”、“整体高可用性”上的度量,且取值越大代表该方案在该维度上越优秀,则对于个体集合{1,2,3,4}来说,每个元素都至少存在另外一个在各方面比自身优秀的个体,如对于个体4来说,个体5在“使用物理机数量”、“整体高可用性”上的维度上都优于个体4,此时我们说“个体5是支配个体4的”;而对于集合{5,6,7}来说,因为不存在支配他们的个体,所以他们被称为“非支配解”;这种“非支配解”的适应度在理论上应该是最高的。
遗传操作设计
遗传算法中的核心操作便是“选择”、“基因交叉”、“基因变异”,这三个操作决定了种群的进化方向,是让算法朝着我们的目标不断优化的基础。
“选择”(Selection):采用2-约束竞赛选择法,在该方法中,从当前种群中随机挑选两个个体,然后将适应值最大的个体作为父个体,不断重复该操作,直到个体数量达到预定的种群规模,选出的父个体作为下一代种群.两个个体的比较方法采用NSGA2引入的拥挤比较算子。
“交叉”(Crossover):挑选两个“选择”过程中被选定的父个体作为交叉对象A、B,随机选择A中的物理机a,将该物理机a放入B中,同时将B个体中包含a的虚拟机序列的原物理机从B中删除,同时记录被删除的虚拟机再次放置到B上。该操作实现了某台物理机的虚拟机序列重分配,且因为物理机的挑选是随机的,确保了“交叉”的多样性;
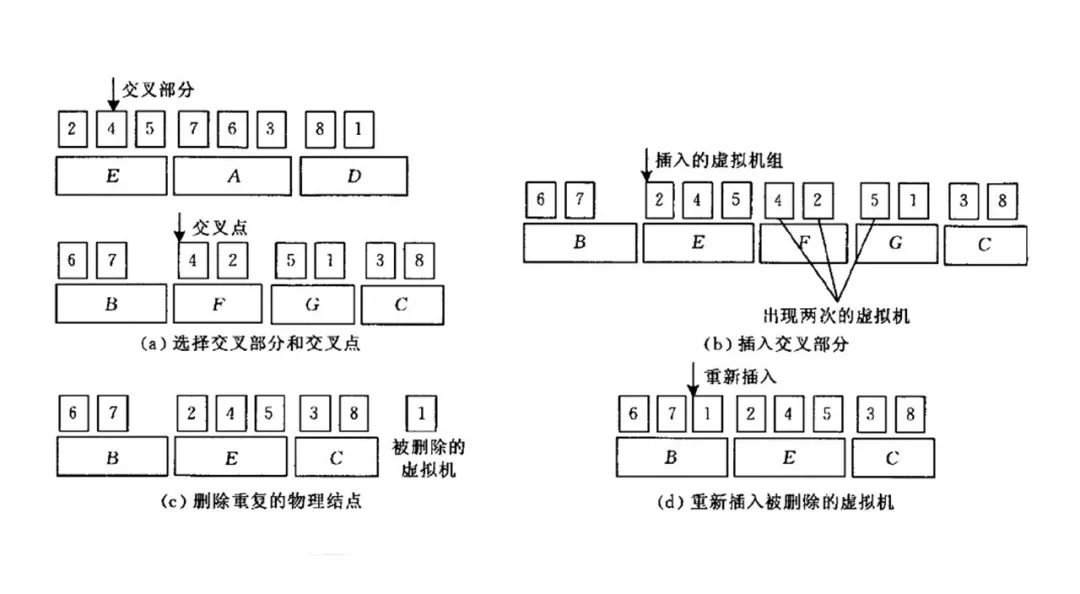
“变异”(Mutation):“变异”的操作相对简单,且具有易懂的解释性:从父个体中随机挑选一个染色体A,然后从个体A上随机挑选一个物理机a,将其删除,并将原来a上的虚拟机序列重新插入到A中——这样的目的是为了减少物理机的使用,但由于物理机a是随机挑选的,其并不能保证每次变异的方向都是对的,因此我们可以降低“变异”操作发生的概率,而且这也正体现出了正确的“选择”的重要性。
控制参数设定
参数设定主要是指在遗传操作中各操作的发生概率,如:我们可以设定“交叉”操作的发生概率为0.6,“变异”操作的发生概率为0.05;有效的参数设定可以控制种群更快、更好的给出近似最优解。
通过实现以上五个要素,我们便可以根据遗传算法的固定步骤,进行虚拟机放置问题的求解了。
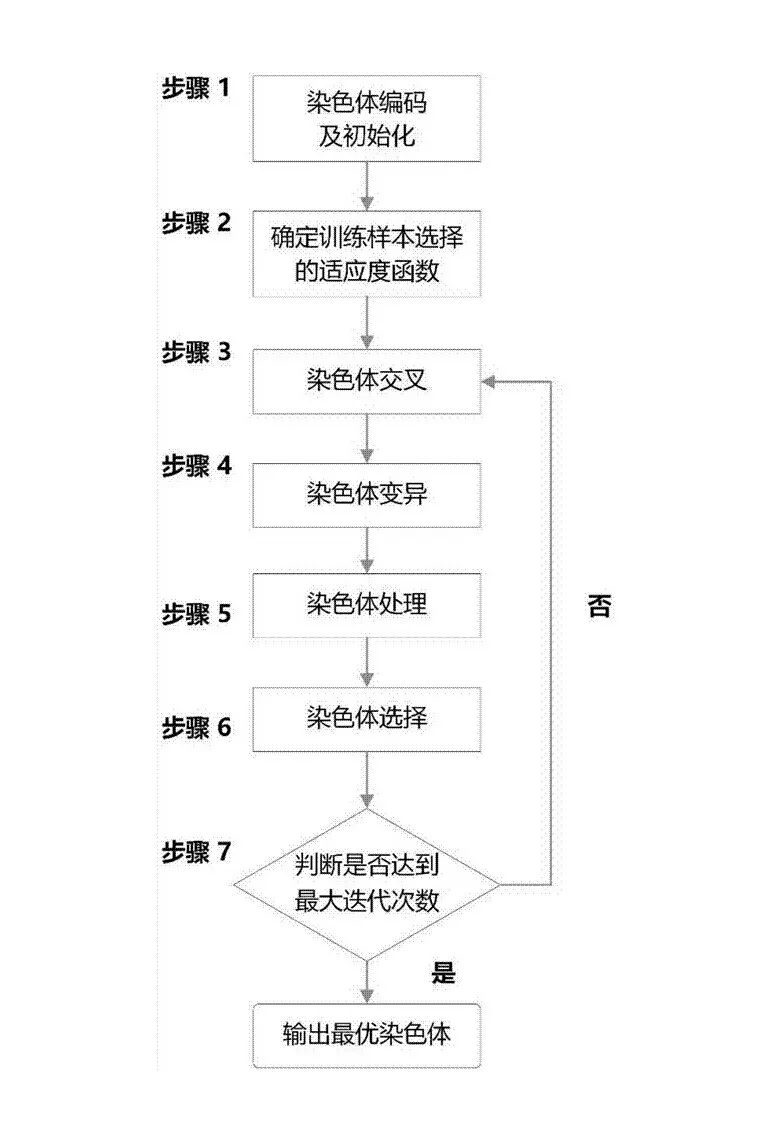
一般来说,跳出算法迭代的条件有两个:一是当前最优染色体的适应值已满足目标设定值,二是达到指定的迭代次数。通过人为经验选择合理的遗传操作策略,我们便可以快速得到我们目标方案。


用AIOps更有效地进行微服务排障
青铜到王者晋级之战 夏洛克AIOps从容应对千百万级别的告警风暴
Gartner中国ICT成熟度曲线发布 擎创成AIOps领域重点推荐服务商

擎创科技简介
擎创科技,成立于2016年,是国内首家智能运维 AIOps落地解决方案的供应商。公司专注于将人工智能赋能运维管理,发掘运维数据的潜在价值,推动企业数字化转型。公司的核心产品夏洛克AIOps,能够结合客户的实际需求,通过人工智能和大数据等技术,实现指标异常检测和趋势预测、故障根因界定和定位、日志智能聚类等智能化分析功能。产品已在中国银联、交通银行、太平洋保险、方正证券、东方航空集团等行业标杆企业落地,覆盖银行、保险、证券、制造及交通等多个行业。擎创科技总部位于上海,并在北京和深圳成立了办事处。

)


)
)

)


)







)
--GET接收指令)