
上一篇我们手写了HashMap,还有一个很重要的Map的实现类TreeMap。打开源码第一句话:* A Red-Black tree based {@link NavigableMap} implementation.TreeMap是一个基于红黑树的实现。对红黑树没有了解怎么办,那就先搞清楚红黑树的原理。只要理解红黑树的玩法,TreeMap实现起来就没有那么大的难度了。
红黑树(Red Black Tree) 是一种自平衡二叉查找树。所以我们先搞明白什么是二叉查找树和完美平衡二叉树。
二叉排序树(Binary Sort Tree)是具有下列性质的二叉树:
- 元素以关键字为依据,每个结点可比较大小,各元素关键字互不相同。
- 对于每个结点,其左子树上所有结点均小于该结点,右子树上所以结点均大于该结点。
- 每个结点的左右子树也分别为二叉排序树。
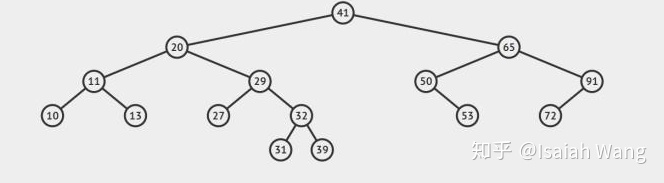
- 查找:从根结点开始查找,根据每一次比较结果,在当前结点的左子树与右子树选择其一,从而缩小一半的查找范围。如果到达叶子结点仍然不相等,则查找不成功。
- 插入:首先使用查找算法确定元素的插入位置。如果查找成功,说明相同元素已经存在,则不插入;否则在查找不成功的一条路径之尾插入结点,作为叶子结点。
- 删除:a. 叶结点直接删除 b. 如果被删除的结点有一个子结点,将子结点移到被删除的元素的位置。c. 采用中序遍历(左-根-右),找到待删除的结点的后继结点,将其与待删除的结点互换,然后删除待删除的结点。假如我们要删除29,中序遍历结果为10-11-13-20-27-29-31-32-39-41-53-50-65-72-91,所以29的后继结点是31,然后互换位置,删除29。
- 二叉查找树的查询复杂度,和二分查找一样,插入和查找的时间复杂度均为 O(logn) ,但是在最坏的情况下仍然会有 O(n) 的时间复杂度。原因在于插入和删除元素的时候,树没有保持平衡。
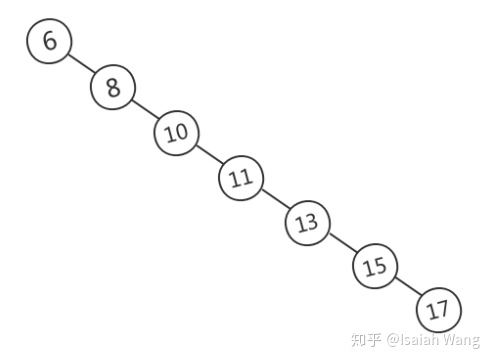
为了降低二叉排序树的高度,提高查找效率。平衡二叉树(又称为AVL树)。平衡二叉树(Balanced Binary Tree)是具有下列性质的二叉排序树:
- 左子树和右子树都是平衡二叉树
- 左子树与右子树高度差绝对值不超过一。结点的平衡因子定义为其左子树与右子树的高度之差。
- 在平衡二叉树中,插入或删除一个结点可能破坏二叉树的平衡性,因此在插入或删除时都要调整二叉树。
插入:如果插入一个结点后破坏了二叉树的平衡性,需要调整一棵最小不平衡子树。最小不平衡子树是离插入结点最近,且以平衡因子绝对值大于1的结点为根的子树。若出现不平衡,则要根据新插入的结点与最低不平衡结点的位置关系进行相应的调整。分为LL,RR,LR,RL四种类型。以下只介绍了最简单的情况。
LL型:在最低不平衡结点的左孩子的左子树上插入结点。插入C后,A的平衡因子由1增加到2 。结点B变成新的根结点。A变成右孩子结点,C变成左孩子结点。
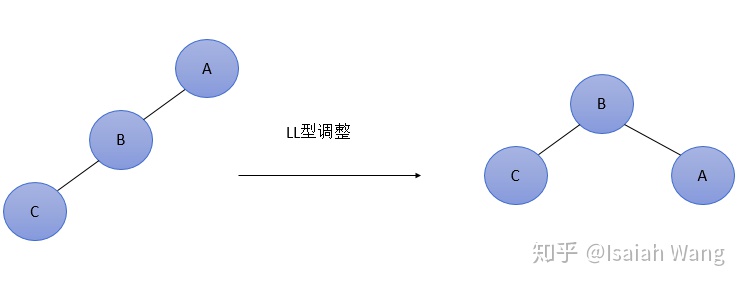
RR型:在最低不平衡结点的右孩子的右子树上插入结点。结点B变成新的根结点。C变成右孩子结点,A变成左孩子结点。
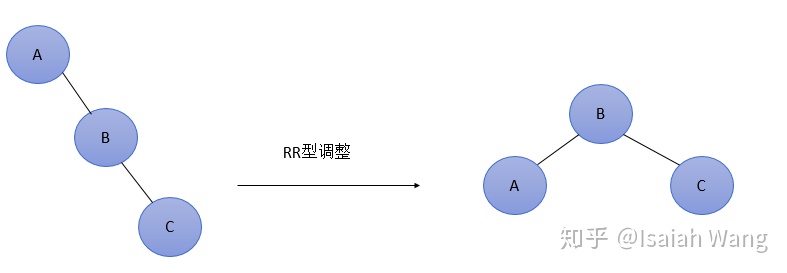
LR型:在最低不平衡结点的左孩子的右子树上插入结点。结点C变成新的根结点。A变成右孩子结点,B变成左孩子结点。
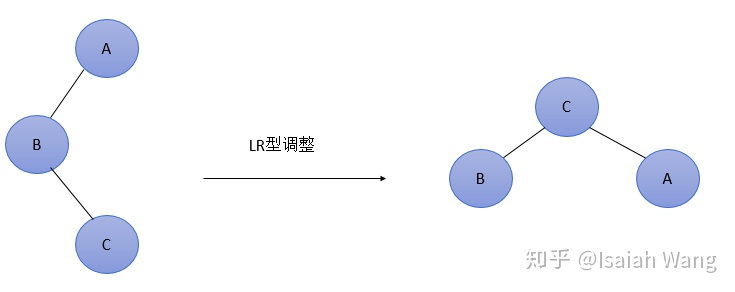
RL型:在最低不平衡结点的右孩子的左子树上插入结点。结点C变成新的根结点。B变成右孩子结点,A变成左孩子结点。
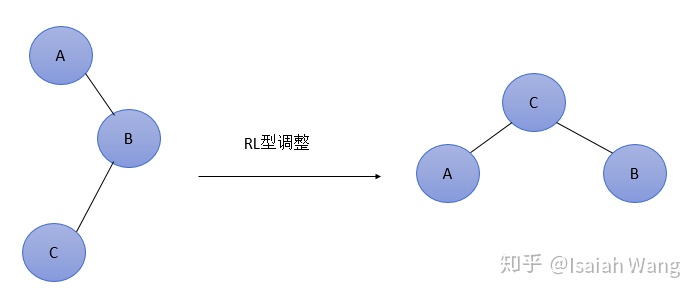
平衡二叉树似乎完美解决了二叉排序树的问题,通过旋转使树的高度最小化,对于有 n 个节点的平衡树,最坏的查找时间复杂度也为 O(logn)。
那么我们为什么还需要红黑树?
因为我们不仅仅需要关心查找的效率,还要考虑插入的效率。因为平衡二叉树要求每个节点的左子树和右子树的高度差至多等于1,这个要求非常严格,每次进行插入/删除数据的时候,几乎都会破坏这个规则。在插入/删除数据很频繁的场景中,平衡二叉树的性能就会受到很严重的影响。所以我们需要红黑树。
红黑树的定义
- 每个节点或者是黑色,或者是红色。
- 根节点是黑色。
- 每个叶子节点是黑色。
- 如果一个节点是红色的,则它的子节点必须是黑色的
- 从任意一个节点到叶子节点,经过的黑色节点是一样的。
- 查找:红黑树的查找和二叉排序树一样,不再赘述
- 添加:
这是一个把数据结构可视化的网站,我们用网站进行一些插入数据的试验Red/Black Tree Visualizationwww.cs.usfca.edu

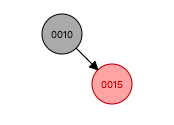
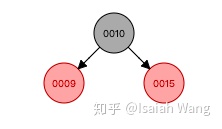
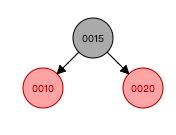
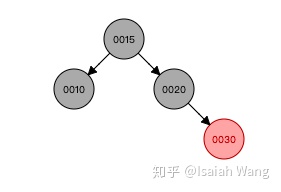
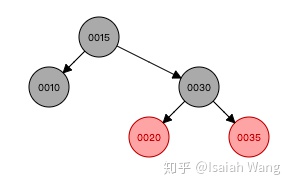
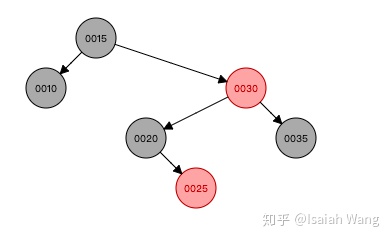
所以我们发现每一次插入数据之后,如果不满足红黑树的定义,就需要对红黑树的结构进行调整。两种方式:旋转和重新上色。所以我们在Java源码中找到了添加数据的方法,并分析这个方法。
/**
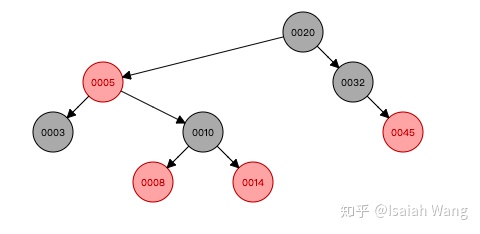
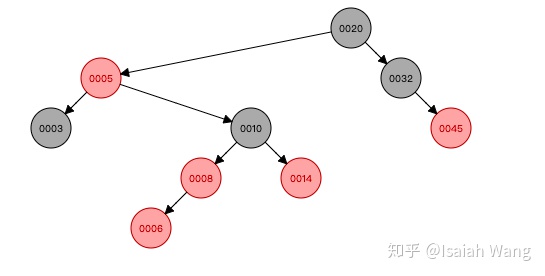
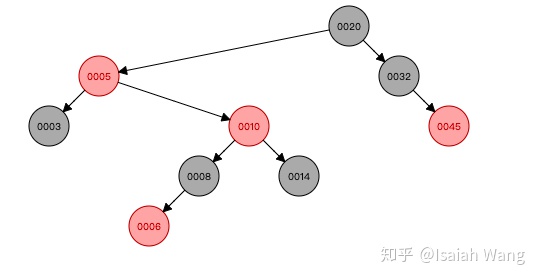
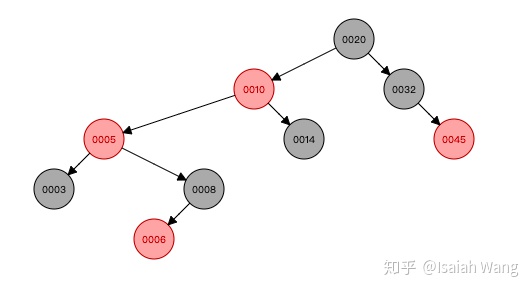
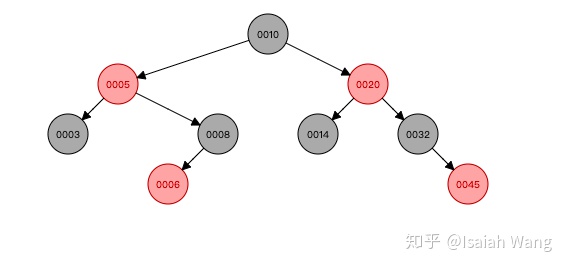
从源码中看出,情况2是情况3的一种扩展。情况4、5、6是1、2、3的镜像,就不展开了。
删除也需要调整树的结构,但是更复杂一些,我们看一下源码中的方法。
/**
删除一共8种情况,1-4和5-8也是镜像的,就不举具体的例子了。TreeMap果然要比HashMap还要复杂的多,就算读懂了 rebalance的方法,真正实现起来还是有很大的难度。以此为基础,下一篇我们尝试一下手写HashMap。

)



)
)




)


)
:字符串转换整数 (atoi))



