LeetCode 2132. 用邮票贴满网格图（DP/二维差分）

文章目录

- 1. 题目
- 2. 解题

1. 题目

给你一个 m x n 的二进制矩阵 grid ，每个格子要么为 0 （空）要么为 1 （被占据）。

给你邮票的尺寸为 stampHeight x stampWidth 。我们想将邮票贴进二进制矩阵中，且满足以下限制和要求：

覆盖所有空 格子。
不覆盖任何 被占据 的格子。
我们可以放入任意数目的邮票。
邮票可以相互有重叠部分。
邮票不允许 旋转。
邮票必须完全在矩阵内。

如果在满足上述要求的前提下，可以放入邮票，请返回 true ，否则返回 false 。

示例 1：
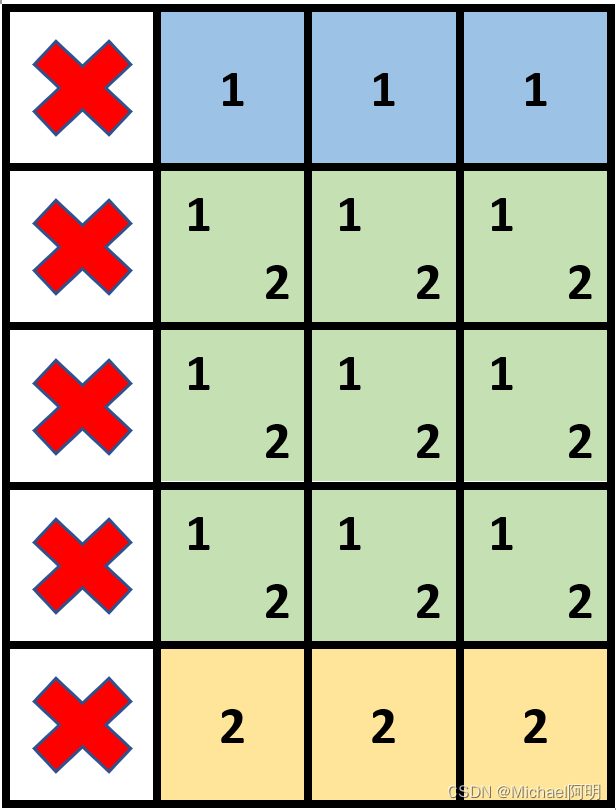
在这里插入图片描述

输入：grid = [[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0],[1,0,0,0]], 
stampHeight = 4, stampWidth = 3
输出：true
解释：我们放入两个有重叠部分的邮票（图中标号为 1 和 2），它们能覆盖所有与空格子。

示例 2：
在这里插入图片描述

输入：grid = [[1,0,0,0],[0,1,0,0],[0,0,1,0],[0,0,0,1]], 
stampHeight = 2, stampWidth = 2 
输出：false 
解释：没办法放入邮票覆盖所有的空格子，且邮票不超出网格图以外。提示：
m == grid.length
n == grid[r].length
1 <= m, n <= 10^5
1 <= m * n <= 2 * 10^5
grid[r][c] 要么是 0 ，要么是 1 。
1 <= stampHeight, stampWidth <= 10^5

来源：力扣（LeetCode）链接：https://leetcode-cn.com/problems/stamping-the-grid
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

2. 解题

DP 的方法求矩形区域内的 1 的数量
如果邮票区域内的 1 的数量为 0，则用差分方法（看的题解区做法）记录这个区域访问过（左上角、右下角+1，另外两角 -1），再最后DP求差分的二维前缀和，前缀和为0则，该位置没有被访问过

class Solution {
public:bool possibleToStamp(vector<vector<int>>& grid, int stampHeight, int stampWidth) {int m = grid.size(), n = grid[0].size();vector<vector<int>> dp(m+1, vector<int>(n+1, 0));vector<vector<int>> diff(m+2, vector<int>(n+2, 0));for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j])dp[i+1][j+1] = 1+dp[i][j+1]+dp[i+1][j]-dp[i][j];elsedp[i+1][j+1] = dp[i][j+1]+dp[i+1][j]-dp[i][j];}} // 求 区域内 1 的数量for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){if(grid[i][j] || i+stampHeight > m || j+stampWidth > n) continue;int outsidearea = dp[i+stampHeight][j]+dp[i][j+stampWidth]-dp[i][j];// i, j 处为左上角，开始贴邮票，邮票之外的 1 的数量int allarea = dp[i+stampHeight][j+stampWidth];// 邮票右下角到地图左上角的 1 的数量if(allarea == outsidearea) // 邮票区域内 没有 1，可以贴{diff[i+1][j+1] += 1; // 差分法记录 该区域的访问情况diff[i+1][j+stampWidth+1] -= 1;diff[i+stampHeight+1][j+1] -= 1;diff[i+stampHeight+1][j+stampWidth+1] += 1;}}}for(int i = 0; i < m; ++i){for(int j = 0; j < n; ++j){diff[i+1][j+1] += diff[i+1][j]+diff[i][j+1]-diff[i][j];// 差分的二维前缀和if(grid[i][j]==0 && diff[i+1][j+1]==0) return false;// 没有 1， 且 没有被邮票访问过，不能贴满}}return true;}
};