一、数据预处理——数据归一化 & 数据标准化
点击标题即可获取文章相关的源代码文件哟!
1.1 数据无量纲化
在机器学习算法实践中,我们往往有着将不同规格的数据转换到同一规格,或不同分布的数据转换到某个特定分布的需求,这种需求统称为将数据“无量纲化”。譬如梯度和矩阵为核心的算法中,譬如逻辑回归,支持向量机,神经网络,无量纲化可以加快求解速度;而在距离类模型,譬如K近邻,K-Means聚类中,无量纲化可以帮我们提升模型精度,避免某一个取值范围特别大的特征对距离计算造成影响。(一个特例是决策树和树的集成算法们,对决策树我们不需要无量纲化,决策树可以把任意数据都处理得很好。)
数据的无量纲化可以是线性的,也可以是非线性的。线性的无量纲化包括
中心化(Zero-centered或者Mean-subtraction)处理和缩放处理(Scale)。
- 中心化的本质是让所有记录减去一个固定值,即让数据样本数据平移到某个位置。
- 缩放的本质是通过除以一个固定值,将数据固定在某个范围之中,取对数也算是一种缩放处理。
一、数据归一化
- preprocessing.MinMaxScaler
当数据(x)按照最小值中心化后,再按极差(最大值 - 最小值)缩放,数据移动了最小值个单位,并且会被收敛到[0,1]之间,而这个过程,就叫做数据归一化(Normalization,又称Min-Max Scaling)。注意,Normalization是归一化,不是正则化,真正的正则化是regularization,不是数据预处理的一种手段。归一化之后的数据服从正态分布,公式如下:
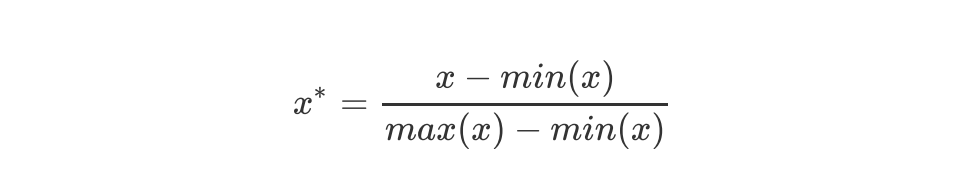
在sklearn当中,我们使用preprocessing.MinMaxScaler来实现这个功能。MinMaxScaler有一个重要参数,feature_range,控制我们希望把数据压缩到的范围,默认是[0,1]。



二、数据标准化
-
preprocessing.StandardScaler
当数据(x)按均值(μ)中心化后,再按标准差(σ)缩放,数据就会服从为均值为0,方差为1的正态分布(即标准正态分布),而这个过程,就叫做数据标准化(Standardization,又称Z-score normalization),公式如下:
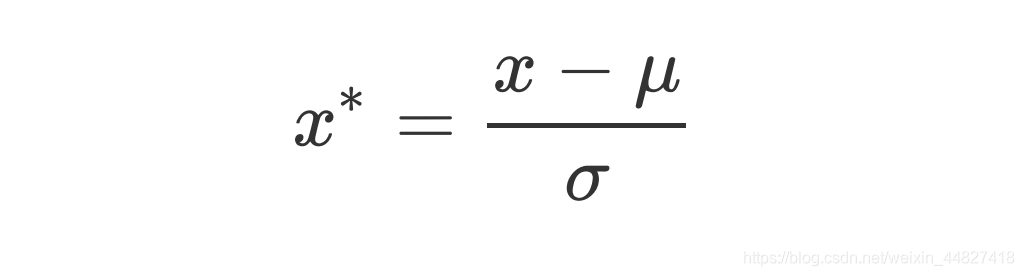


对于StandardScaler和MinMaxScaler来说,空值NaN会被当做是缺失值,在fit的时候忽略,在transform的时候保持缺失NaN的状态显示。并且,尽管去量纲化过程不是具体的算法,但在fit接口中,依然只允许导入至少二维数组,一维数组导入会报错。通常来说,我们输入的X会是我们的特征矩阵,现实案例中特征矩阵不太可能是一维,所以不会存在这个问题。 -
StandardScaler和MinMaxScaler选哪个?
看情况。大多数机器学习算法中,会选择StandardScaler来进行特征缩放,因为MinMaxScaler对异常值非常敏感。在PCA,聚类,逻辑回归,支持向量机,神经网络这些算法中,StandardScaler往往是最好的选择。
MinMaxScaler在不涉及距离度量、梯度、协方差计算以及数据需要被压缩到特定区间时使用广泛,比如数字图像处理中量化像素强度时,都会使用MinMaxScaler将数据压缩于[0,1]区间之中。
建议先试试看StandardScaler,效果不好换MinMaxScaler。
除了StandardScaler和MinMaxScaler之外,sklearn中也提供了各种其他缩放处理(中心化只需要一个pandas广播一下减去某个数就好了,因此sklearn不提供任何中心化功能)。比如,在希望压缩数据,却不影响数据的稀疏性时(不影响矩阵中取值为0的个数时),我们会使用MaxAbsScaler;在异常值多,噪声非常大时,我们可能会选用分位数来无量纲化,此时使用RobustScaler。更多详情请参考以下列表。



)








...)




)
)

