总谐波失真计算公式_新能源汽车技术|车用轮毂电机转矩谐波协同控制策略

点击电机与控制应用 · 关注我们

轮毂电机因结构简单、驱动灵活的特点广泛应用于轻型电动车辆。电机运行中存在的齿槽效应、逆变器非线性效应及电流谐波等问题，导致电机电磁转矩波动，影响车辆运行的平顺性。通过电磁转矩谐波分析发现其主要成分为低阶谐波。为了有效抑制低次转矩谐波，设计了一种附加三相独立定子绕组的轮毂电机结构，提出了基于电流幅值迭代整定的补偿电流注入方法，采用动态步长二分法实现期望补偿电流幅值的快速收敛。研究结果表明，所提方法可使总谐波失真降低2.80%~5.84%，具有良好的谐波转矩抑制效果。

车用轮毂电机转矩谐波协同控制策略

郑凯达1，王子辉2，何致远2

(1. 浙江科技学院机械与能源工程学院，浙江杭州 310023；2. 浙江科技学院自动化与电气工程学院，浙江杭州 310023)

0 引言

在轻型电动车辆中，轮毂电机技术因具有高效率、节省空间、易控制、低成本、模块化等优点，成为许多电动车辆的选择[1]。由于逆变器非线性、转子面轴承同轴度不良、齿槽效应等因素，车用永磁轮毂电机运行时存在转矩波动，导致车辆运行中产生噪声和振动，影响驾驶的舒适性和平顺性。针对永磁电机转矩谐波的问题，目前国内外研究动态通常从电机本体磁路设计和驱动控制2方面实施补偿和优化。Bonthu等[2]提出一种基于槽型和转子磁通势垒设计的转子形状优化方案，对外转子电机进行结构上的优化设计，采用了一种优化外转子开槽形状的方法，试验证明可减少转矩脉动。唐旭等[3]通过在定子上开辅助槽的方式，使得磁极与齿槽之间的齿槽谐波频率增加，降低了齿槽转矩的幅值。邱壮飞[4]针对中低速无刷直流电机换相转矩波动，以相电流为控制对象，提出了一种三相电流滞环跟踪的控制策略，并运用恒频电流控制技术使逆变器保持固定开关频率，以抑制无刷直流电机换相转矩波动。姜茹等[5]基于矢量控制原理，提出了一种补偿滞后相位的脉宽调制(PWM)基波电压的控制方法，可提高系统动态响应速度，并降低转矩波动。阮鹏等[6]针对永磁同步电机(PMSM)定子谐波电流的问题，设计了一种基于一阶线性自抗扰的控制方法，实现对谐波电流的抑制。针对气隙磁场不均匀所造成的转矩波动问题，Shakouhi等[7]提出了一种基于反电动势估计的在线控制方法，通过FFT分析提取高频电流电压分量，采用容错控制策略降低了静态偏心产生的转矩脉动。上述优化控制方法可对特定因素造成的转矩谐波进行独立补偿，以获得更好的谐波抑制效果，但在实际运行中，电机系统的结构特性、磁路特性和开关器件特性同时作用于电磁转矩，转矩谐波成分相互耦合，分析和控制过程较为复杂。传统的定子绕组补偿电流注入方法通常从定子绕组中提取电流信号，经傅里叶分析提取基波电流中谐波分量并设计控制策略抑制谐波成分。然而在电动汽车运行过程中，轮毂式PMSM会产生较大的基频电流，导致高频谐波电流与基频电流比值过小，谐波电流提取困难，难以实现有效控制。因此，研究轮毂电机电磁谐波转矩协同控制策略具有重要意义。本文以外转子轮毂PMSM作为研究对象，分析输出转矩的谐波成分，针对性地补偿幅值较大的谐波阶次，利用电磁转矩周期性变化的特点，迭代计算最优补偿电流幅值，向附加绕组注入幅值、频率、相位可控的补偿电流，以有效抑制转矩脉动。1 电磁转矩谐波分析在dq坐标系下，外转子永磁轮毂电机的电磁关系表示为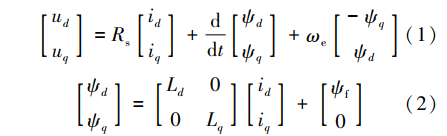

式中：ud、uq为dq坐标系下定子电压；Rs为定子电阻；id、iq为dq坐标系下定子电流；ψd、ψq为dq坐标系下定子磁链；ωe为转子电角速度；Ld、Lq为dq坐标系下定子电感。在dq坐标系下电磁转矩表达式为

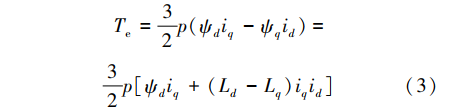式中：p为电机极对数。PMSM转子运动方程可表示为

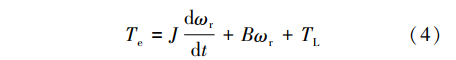式中：J为转动惯量；ωr为转子机械角速度；B为黏滞系数；TL为负载转矩。车用轮毂式PMSM在实际工况下运行会产生转矩波动，所造成的原因可概括为(1)换相时刻电力电子器件的非线性因素造成的转矩谐波；(2)电机齿槽效应导致的转矩谐波；(3)电机气隙磁场分布的非正弦性引起的转矩波动。换相时刻电力电子器件的非线性，例如开关器件的死区时间和管压降等问题，造成逆变器输出电压畸变，相电流包含低阶奇次谐波和开关频率及其倍数次的高阶谐波[8]。考虑谐波影响下的电机转矩计算式可表示为

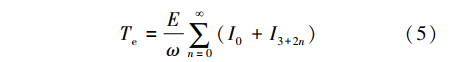式中：E为反电动势；ω为转子机械角速度。式(5)中出现奇次谐波电流，主要成分为5次和7次谐波电流，转矩谐波阶次与电流谐波阶次相关。轮毂电机因制造工艺原因或在复杂路面工况下受到地形激励时，会造成定转子间的偏心。偏心工况下电机转矩式可表示为

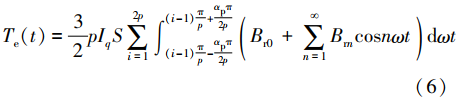式中：S为磁通面积；αp为永磁体极弧系数；Brn为各阶次永磁体剩磁密度。由文献[9-10]分析得出，偏心电机非均匀分布的气隙磁密导致电磁转矩产生波动，偏心电机靠近气隙最小处的磁密增加明显，随着偏心的增大，气隙磁密谐波畸变率不断增大会使电磁转矩波形发生严重畸变，偏心大小与气隙磁通密度畸变程度成正相关。齿槽转矩的产生是由定转子铁心齿槽的存在，存储在气隙中的磁场能量不均匀分布导致的[11]。由文献[12]得到齿槽转矩的表达式为

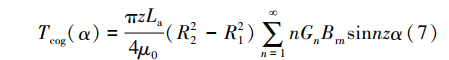式中：α为定转子相对位置角；z为电机槽数；La为电枢铁心轴向长度；R1、R2为电枢外半径和定子轭内半径；Gn为有效气隙磁导圆周分布函数。齿槽转矩以一个槽距(或齿距)为周期重复，当谐波阶次满足nz/(2p)为整数时才会产生齿槽转矩，并随着阶次的升高，转矩幅值降低。由上述分析可知，在不同工况下电机转矩谐波的产生机理、谐波阶次不同，且实际应用中多工况互相影响，各种谐波成分间存在耦合作用，难以协同分析和控制，因此引入三相附加绕组的补偿控制策略，以实现多工况下转矩谐波的协同补偿。2 三相附加绕组电磁转矩补偿2.1 补偿原理分析补偿转矩谐波的原理是在电机原有定子绕组上加入一套如图1所示的Y型连接的三相对称绕组，该绕组与定子绕组电气绝缘。通过向三相附加绕组中通入补偿电流，产生与转矩谐波相位相反的电磁转矩，消除转矩谐波成分。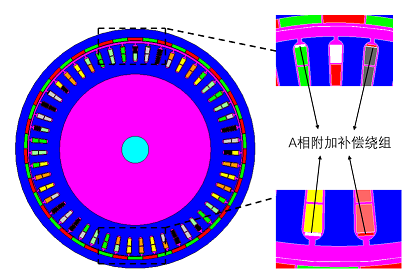

图1 补偿绕组示意图取补偿电流

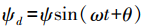，电流幅值余弦变化，空间固定。取磁链

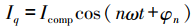，磁链幅值恒定，空间旋转。在dq坐标系下，绕组产生的电磁转矩表示为

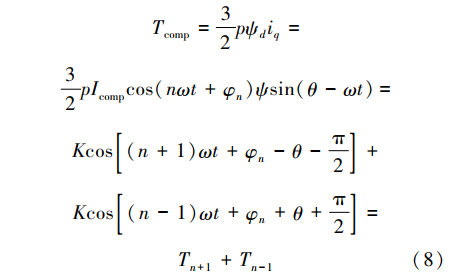式中：ψd为永磁体产生的磁链；θ为转子初始相位角；φn为相位。由式(8)第3项可知，通入n次补偿电流，可补偿n+1次和n-1次的转矩谐波。电机在实际工况下的转矩输出可表示为

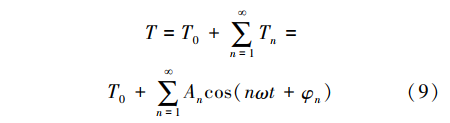式中：T0代表输出转矩的直流分量；

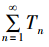代表谐波分量。将式(9)谐波分量与式(8)相对应，可得到补偿电流的特征值。需要指出当n=1时，由式(8)可以看出在注入补偿电流后，附加绕组除补偿2阶谐波外，还对电机出力效率略有影响。2.2 补偿控制系统设计基于补偿电流注入的控制系统如图2所示。由式(4)可知，电磁转矩的波动会引起电机转速的波动。根据电机转速计算得到电机的电磁转矩，经过FFT分析，获取电磁转矩所含的谐波分量特征值。

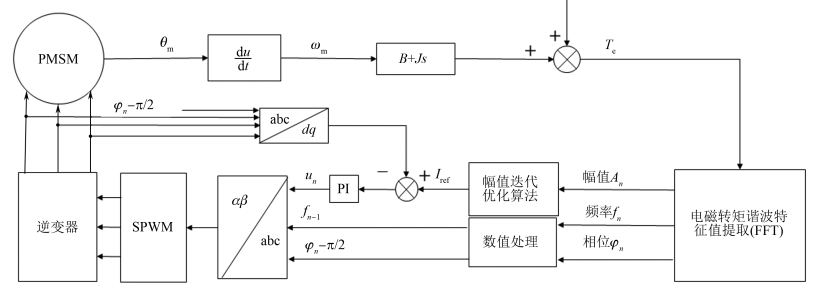图2 基于电流注入的转矩补偿控制系统由式(8)可知，为了抑制n次电磁转矩波动，需向补偿绕组注入n-1次谐波电流，其相位依赖转子与补偿绕组的初始位置，而幅值则与磁链值有关。考虑磁链谐波的气隙磁链可表示为

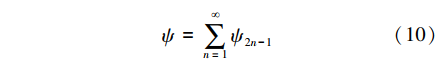磁链ψ以其谐波随工况变化，不易观测获得。注入的电流与产生的转矩为非线性关系，求解复杂，采用迭代算法求解较为简便。利用电机输出电磁转矩具有周期性的特点，运用迭代优化的算法求解补偿电流幅值，给定初始电流幅值Ik=0，通入电流后的转矩谐波幅值为f(Ik)。为了快速确定搜索区间，以λ为计算步长，迭代计算接近搜索区间［a0,b0］。为了在搜索区间内得到精确的补偿电流幅值，将搜索区间通过0.618这个迭代步长系数分成2个区间，其中较大的一个区间与整个区间的比值和较小的一个区间与较大的一个区间的比值是相等的，能够使区间缩小速度最快[13]。选取0.618作为迭代步长系数，ε作为迭代终止条件，逐次逼近极值区间并在误差小于ε时终止迭代，求得最优补偿电流幅值I。具体程序算法流程设计如图 3所示。

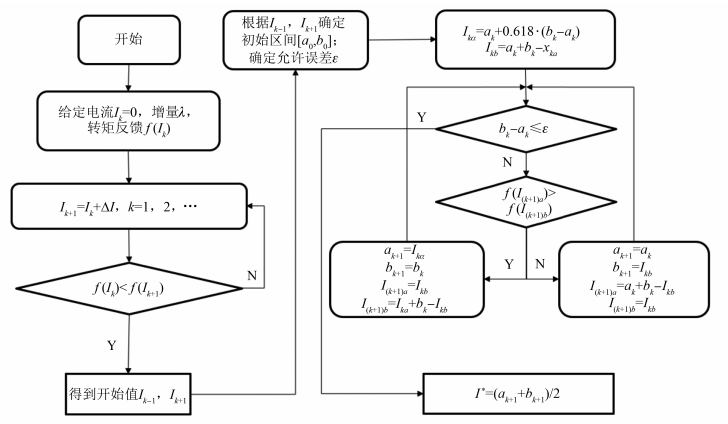图3 补偿电流幅值寻优过程3 仿真与试验研究3.1 仿真研究基于FLUX/MATLAB环境，在逆变器非线性与定转子偏心的2种工况下，建立带有补偿绕组的51槽46极轮毂PMSM模型，对电机模型进行仿真研究。电机参数如表1所示。

表1 电机参数

对电磁转矩实施FFT变换，获得各阶谐波的幅值、频率阶次特征值如图4所示。图4(a)表明，逆变器非线性工况下6次谐波占比最高，静偏心时根据图4(b)的谐波分析可知占比最高为2次谐波，可知在2种工况下，对电磁转矩影响最显著的为上述2种阶次的转矩谐波。

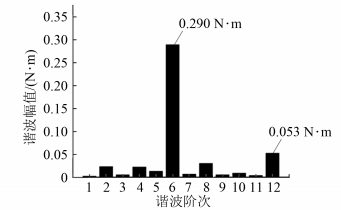
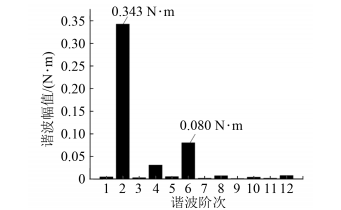
(a)逆变器非线性转矩谐波分析

(b)偏心电机转矩谐波分析

图4 电磁转矩谐波分析基于上述2种工况，根据FFT分析获得的转矩幅值、频率阶次、相位，结合式(6)、式(7)，获得补偿电流特征值，向补偿绕组通入5倍频电流以补偿6次转矩谐波，通入1倍频电流以补偿2次转矩谐波，得到2种工况下补偿前后的转矩谐波幅值如图5所示。图5(a)表明，补偿6次谐波幅值时，谐波幅值由0.289 53 N·m减小至0.080 4 N·m，降低了72.23%；图5(b)表明，补偿2次谐波时，谐波幅值由0.342 6 N·m降至0.082 4 N·m，降低了76.532 4%，2种补偿方式都有效降低了转矩谐波的幅值。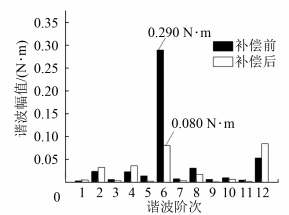

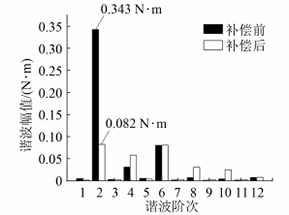
(a)逆变器非线性补偿

(b)偏心电机补偿

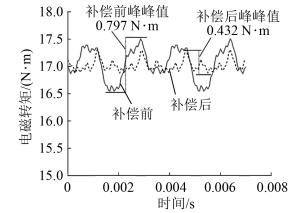
图5 电磁转矩谐波幅值补偿效果图图6给出了2种工况下，补偿前后的电磁转矩波形。由图6可知，2种工况下补偿前转矩波形均较不平滑。图6(a)可发现，注入补偿电流后，转矩波形的峰峰值由0.835 N·m减小到0.251 N·m，减小了69.94%。图6(b)可观察到在偏心工况下，通入补偿电流后的转矩波形的峰峰值由0.797 N·m减小到0.432 N·m，减小了45.80%。2种工况下补偿后的转矩波形均比补偿前更趋平滑。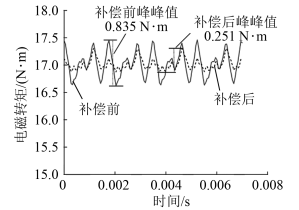

(a)逆变器非线性补偿波形

(b)偏心电机补偿波形

图6 电磁转矩补偿波形效果图表2为电磁转矩各阶次谐波的补偿前后幅值对比。前12阶次转矩谐波和与转矩直流分量的比值为总谐波失真THD，由表2计算可得补偿前后的总谐波失真变化。在逆变器非线性工况时，通入补偿电流后，总谐波失真THD由2.56%降至1.79%。在静偏心工况时，补偿后的总谐波失真THD由2.20%降至0.84%，2种工况下谐波总量均减小。

表2 各阶次谐波幅值补偿仿真对比表

3.2 试验研究试验平台由测功机、轮毂电机样机、电机驱动系统、补偿绕组电源组成，如图7所示。附带补偿绕组的轮毂电机参数同表1。

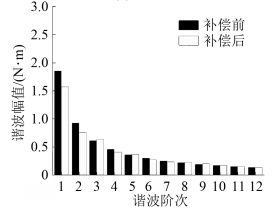
图7 轮毂电机转矩测试平台在300 r/min转速下通入补偿电流，得到补偿前后转矩波形和谐波幅值如图8所示。由图8(a)可知，补偿前轮毂电机在实际运行时受复杂工况影响，输出电磁转矩中，谐波成分占比高，以低次谐波为主。补偿后的转矩峰峰值由2.46 N·m减少到1.92 N·m，减少了22.02%。各阶谐波幅值如图8(b)所示，一阶转矩谐波由1.85 N·m减少到1.57 N·m，减少了15.21%，二阶转矩谐波由0.93 N·m减少到0.76 N·m，减少17.73%，六阶转矩谐波由0.30 N·m减少到0.27 N·m，减少了9.97%。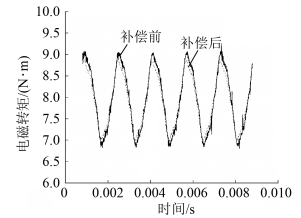

(a)转矩波形

(b)转矩谐波幅值补偿效果

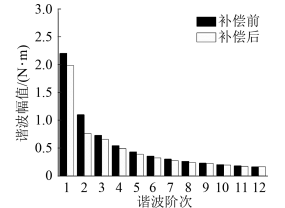
图8 300 r/min转矩谐波补偿效果图在400 r/min转速下通入补偿电流，得到补偿前后转矩波形和谐波幅值如图9所示。由图9(a)可知，补偿后的转矩峰峰值由4.02 N·m减少到2.70 N·m，减少了32.89%。各阶谐波幅值如图9(b)所示，一阶转矩谐波由2.20 N·m减少到1.98 N·m，减少了9.94%，二阶转矩谐波由1.10 N·m减少到0.76 N·m，减少了30.76%，六阶转矩谐波由0.36 N·m减少到0.32 N·m，减少了10.08%。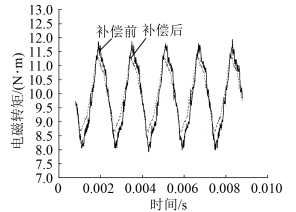

(a)转矩波形

(b)转矩谐波幅值补偿效果

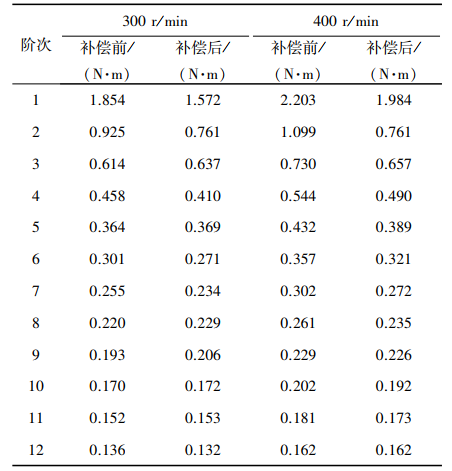
图9 400 r/min转矩谐波补偿效果图表3为补偿前后各阶次转矩谐波幅值。由表3可知，随着转速的升高，电机输出转矩中的各阶次谐波成分也相应增加。由表3计算可得，300 r/min转速时，输出转矩的总谐波失真THD从65.07%降至62.77%；400 r/min转速时，输出转矩的总谐波失真THD从68.08%降至62.24%。结果表明，高转速时转矩谐波补偿效果比低转速时更优，2种转速工况下总谐波失真均减小，验证了该补偿策略的有效性。

表3 各阶次转矩谐波幅值补偿对比表

4 结语本文提出了一种补偿电流注入的转矩波动抑制方法，并建立了注入电流与谐波电磁转矩之间的定量关系。分析外转子轮毂电机在各种工况下的电磁转矩谐波成分，根据不同工况下转矩谐波的特点，提出了一种基于迭代优化算法的补偿电流注入控制策略，用于减少电磁转矩波动。仿真及试验结果表明，该方法可协同抑制多种工况造成的转矩波动，依次抑制电磁转矩中幅值较大的各阶谐波分量，实现改善电机输出转矩平顺性的目的。参考文献详见原文。本文发表于《电机与控制应用》2020年第11期。

Electric Machines & Control Application

广告

苏州市华能发电机有限公司