同学你好!本文章于2021年末编写,获得广泛的好评!
故在2022年末对本系列进行填充与更新,欢迎大家订阅最新的专栏,获取基于Pytorch1.10版本的理论代码(2023版)实现,
Pytorch深度学习·理论篇(2023版)目录地址为:
CSDN独家 | 全网首发 | Pytorch深度学习·理论篇(2023版)目录本专栏将通过系统的深度学习实例,从可解释性的角度对深度学习的原理进行讲解与分析,通过将深度学习知识与Pytorch的高效结合,帮助各位新入门的读者理解深度学习各个模板之间的关系,这些均是在Pytorch上实现的,可以有效的结合当前各位研究生的研究方向,设计人工智能的各个领域,是经过一年时间打磨的精品专栏!https://v9999.blog.csdn.net/article/details/127587345欢迎大家订阅(2023版)理论篇
以下为2021版原文~~~~

1 训练模型的步骤与方法
- 将样本书记输入到模型中计算出正向的结果
- 计算模型结果与样本目标数值之间的差值(也称为损失值loss)
- 根据损失值,使用链式反向求导的方法,依次计算出模型中每个参数/权重的梯度
- 使用优化器中的策略对模型中的参数进行更新
2 神经网络模块中的损失函数
2.1 损失函数定义
损失函数主要用来计算“输出值”与“输入值”之间的差距,即误差,反向传播中依靠损失函数找到最优的权重。
2.2 L1损失函数/最小绝对值偏差(LAD)/最小绝对值误差(LAE)
L1损失函数用于最小化误差,该误差是真实值和预测值之间的所有绝对差之和。
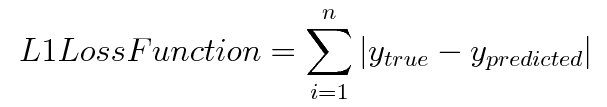
2.2.1 代码实现==>以类的形式进行封装,需要对其实例化后再使用
import torch
### pre:模型的输出值
### label:模型的目标值
loss = torch.nn.L1Loss()[pre,label]2.3 L2损失函数
L2损失函数用于最小化误差,该误差是真实值和预测值之间所有平方差的总和
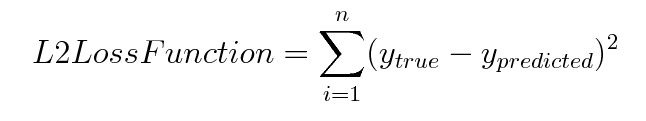
2.4 均值平方差损失(MSE)
均值平方差损失(MSE)主要针对的是回归问题,主要表达预测值域真实值之间的差异
2.4.1 MSE的公式表述
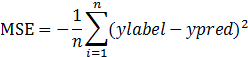
这里的n表示n个样本。ylabel与ypred的取值范围一般为0-1。
2.4.2 注释
- MSE的值越小,表明模型越好
- 在神经网络的计算中,预测值与真实值要控制在相同的数据分布中
- 假设预测值输入Sigmoid激活函数后其取值范围为0到1之间,则真实值的取值范围也应该取到0到1之间
2.4.3 代码实现==>以类的形式进行封装,需要对其实例化后再使用
import torch
### pre:模型的输出值
### label:模型的目标值
loss = torch.nn.MSELoss()(pre,label)2.5 交叉熵损失函数(Cross Entropy)
2.5.1 交叉熵损失函数简介
交叉熵损失函数可以用来学习模型分布与训练分布之间的差异,一般用作分类问题,数学含义为预测输入样本属于某一类别的概率。
2.5.2 公式介绍
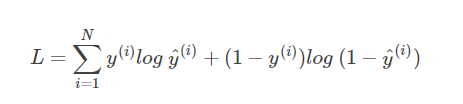
y^为真实分类y的概率值
2.5.3 代码实现==>以类的形式进行封装,需要对其实例化后再使用
import torch
### pre:模型的输出值
### label:模型的目标值
loss = torch.nn.CrossEntropyLoss()(pre,label)2.5.4 图像理解
接下来,我们从图形的角度,分析交叉熵函数,加深大家的理解。首先,还是写出单个样本的交叉熵损失函数:
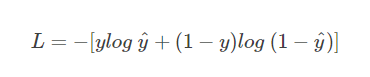
我们知道,当 y = 1 时:
![]()
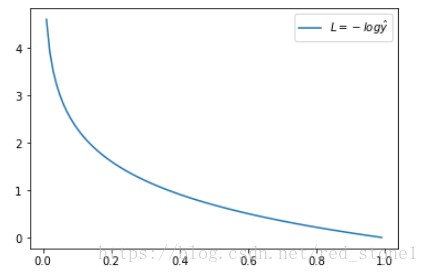
这时候,L 与预测输出的关系如下图所示:
看了 L 的图形,简单明了!横坐标是预测输出,纵坐标是交叉熵损失函数 L。显然,预测输出越接近真实样本标签 1,损失函数 L 越小;预测输出越接近 0,L 越大。因此,函数的变化趋势完全符合实际需要的情况。
当 y = 0 时:
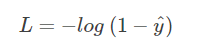
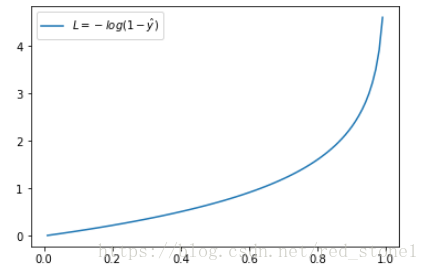
这时候,L 与预测输出的关系如下图所示:
同样,预测输出越接近真实样本标签 0,损失函数 L 越小;预测函数越接近 1,L 越大。函数的变化趋势也完全符合实际需要的情况。
从上面两种图,可以帮助我们对交叉熵损失函数有更直观的理解。无论真实样本标签 y 是 0 还是 1,L 都表征了预测输出与 y 的差距。
从图形中我们可以发现:预测输出与 y 差得越多,L 的值越大,也就是说对当前模型的 “ 惩罚 ” 越大,而且是非线性增大,是一种类似指数增长的级别。这是由 log 函数本身的特性所决定的。这样的好处是模型会倾向于让预测输出更接近真实样本标签 y。
2.6 其他损失函数
2.6.1 SmoothL1Loss
SmoothL1Loss:平滑版的L1损失函数。此损失函数对于异常点的敏感性不如MSE-Loss。在某些情况下(如Fast R-CNN模型中),它可以防止梯度“爆炸”。这个损失函数也称为Huber loss。
2.6.2 NLLLoss
NLLLoss:负对数似然损失函数,在分类任务中经常使用。
2.6.3 NLLLoss22d
NLLLoss22d:计算图片的负对数似然损失函数,即对每个像素计算NLLLoss。
2.6.4 KLDivLoss
KLDivLoss:计算KL散度损失函数。
2.6.5 BCELoss
BCELoss:计算真实标签与预测值之间的二进制交叉熵。
2.6.6 BCEWithLogitsLoss
BCEWithLogitsLoss:带有Sigmoid激活函数层的BCELoss,即计算target与Sigmoid(output)之间的二进制交叉熵。
2.6.7 MarginRankingLoss
MarginRankingLoss:按照一个特定的方法计算损失。计算给定输入x、x(一维张量)和对应的标y(一维张量,取值为-1或1)之间的损失值。如果y=1,那么第一个输入的值应该大于第二个输入的值;如果y=-1,则相反。
2.6.8 HingeEmbeddingLoss
HingeEmbeddingLoss:用来测量两个输入是否相似,使用L1距离。计算给定一个输入x(二维张量)和对应的标签y(一维张量,取值为-1或1)之间的损失值。
2.6.9 MultiLabelMarginLoss
MultiLabelMarginLoss:计算多标签分类的基于间隔的损失函数(hinge loss)。计算给定一个输入x(二维张量)和对应的标签y(二维张量)之间的损失值。其中,y表示最小批次中样本类别的索引。
2.6.10 SoftMarginLoss
SoftMarginLoss:用来优化二分类的逻辑损失。计算给定一个输入x(二维张量)和对应的标签y(一维张量,取值为-1或1)之间的损失值。
2.6.11 MultiLabelSoftMarginLoss
MultiLabelSoftMarginLoss:基于输入x(二维张量)和目标y(二维张量)的最大交叉熵,优化多标签分类(one-versus-al)的损失。
2.6.12 CosineEmbeddingLoss
CosineEmbeddingLoss:使用余弦距离测量两个输入是否相似,一般用于学习非线性embedding或者半监督学习。
2.6.13 MultiMarginLoss
MultiMarginLoss:用来计算多分类任务的hinge loss。输入是x(二维张量)和y(一维张量)。其中y代表类别的索引。
2.7 汇总
用输入标签数据的类型来选取损失函数
如果蝓入是无界的实数值,那么损失函数使用平方差
如果输入标签是位矢量(分类标识),那么使用交叉熵会更适合。













)





