1、问题引入
在统计学中,线性回归是利用称为线性回归方程的最小二乘函数对一个或多个自变量和因变量之间关系进行建模的一种回归分析。这种函数是一个或多个称为回归系数的模型参数的线性组合。一个带有一个自变量的线性回归方程代表一条直线。我们需要对线性回归结果进行统计分析。
例如,假设我们已知一些学生年纪和游戏时间的数据,可以建立一个回归方程,输入一个新的年纪时,预测该学生的游戏时间。自变量为学生年纪,因变量为游戏时间。当只有一个因变量时,我们称该类问题为简单线性回归。当游戏时间与学生年纪和学生性别有关,因变量有多个时,我们称该类问题为多元线性回归。
2、常见的统计量
在研究该问题之前,首先了解下编程中用到的常见的统计量:
序号
概念
公式
算法
说明
1
均值
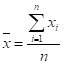
整体的均值
2
中位数
排序后取中间值
3
众数
出现次数最多的数
出现频率
4
方差
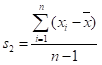
数据的离散程度
5
标准差
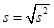
s
方差的开方
2、简单线性回归实例及编程实现
研究一个自变量(X)和一个因变量(y)的关系
简单线性回归模型定义:

简单线性回归方程:
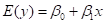
其中:
 为回归线的截距
为回归线的截距
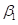 为回归线的斜率
为回归线的斜率
通过训练数据,求取出估计参数建立的直线方程:
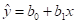
实际编程时,主要是根据已知训练数据,估计出
 和
和
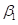 的值
的值
 和
和
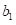
以下面实例为例,第一列表示每月投放广告的次数,第二列表示汽车向量,通过Python编程求取线性回归方程:
投放广告数
汽车销量
1
14
3
24
2
18
1
17
3
27
编程关键在于如何求取b0和b1的值,我们引入一个方程(sum of square):
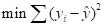
当上述方程的值最小时,我们认为求取到线程回归方程参数的值,对该方程求最小值可以进一步转化为求导和求极值的问题,求导过程省略,最后结论如下:
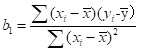
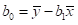
实际代码:
importnumpy as npfrom matplotlib importpylab as pl#定义训练数据
x = np.array([1,3,2,1,3])
y= np.array([14,24,18,17,27])#回归方程求取函数
deffit(x,y):if len(x) !=len(y):returnnumerator= 0.0denominator= 0.0x_mean=np.mean(x)
y_mean=np.mean(y)for i inrange(len(x)):
numerator+= (x[i]-x_mean)*(y[i]-y_mean)
denominator+= np.square((x[i]-x_mean))print('numerator:',numerator,'denominator:',denominator)
b0= numerator/denominator
b1= y_mean - b0*x_meanreturnb0,b1#定义预测函数
defpredit(x,b0,b1):return b0*x +b1#求取回归方程
b0,b1 =fit(x,y)print('Line is:y = %2.0fx + %2.0f'%(b0,b1))#预测
x_test = np.array([0.5,1.5,2.5,3,4])
y_test= np.zeros((1,len(x_test)))for i inrange(len(x_test)):
y_test[0][i]=predit(x_test[i],b0,b1)#绘制图像
xx = np.linspace(0, 5)
yy= b0*xx +b1
pl.plot(xx,yy,'k-')
pl.scatter(x,y,cmap=pl.cm.Paired)
pl.scatter(x_test,y_test[0],cmap=pl.cm.Paired)
pl.show()
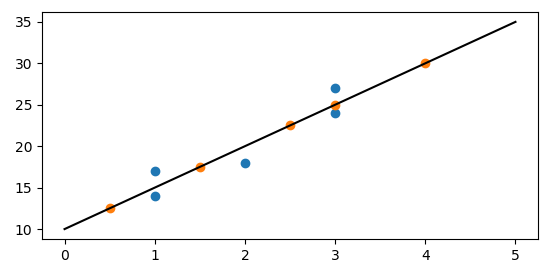
蓝色表示测试数据,橙色表示预测数据。
3、多元线性回归实例及编程实现
多元线性回归方程和简单线性回归方程类似,不同的是由于因变量个数的增加,求取参数的个数也相应增加,推导和求取过程也不一样。
y=β0+β1x1+β2x2+ ... +βpxp+ε
对于b0、b1、…、bn的推导和求取过程,引用一个第三方库进行计算。以如下数据为例,对运输里程、运输次数与运输总时间的关系,建立多元线性回归模型:
运输里程
运输次数
运输总时间
100
4
9.3
50
3
4.8
100
4
8.9
100
2
6.5
50
2
4.2
80
2
6.2
75
3
7.4
65
4
6.0
90
3
7.6
90
2
6.1
代码如下:
importnumpy as npfrom sklearn importdatasets,linear_model#定义训练数据
x = np.array([[100,4,9.3],[50,3,4.8],[100,4,8.9],
[100,2,6.5],[50,2,4.2],[80,2,6.2],
[75,3,7.4],[65,4,6],[90,3,7.6],[90,2,6.1]])print(x)
X= x[:,:-1]
Y= x[:,-1]print(X,Y)#训练数据
regr =linear_model.LinearRegression()
regr.fit(X,Y)print('coefficients(b1,b2...):',regr.coef_)print('intercept(b0):',regr.intercept_)#预测
x_test = np.array([[102,6],[100,4]])
y_test=regr.predict(x_test)print(y_test)
如果特征向量中存在分类型变量,例如车型,我们需要进行特殊处理:
运输里程
输出次数
车型
隐式转换
运输总时间
100
4
1
010
9.3
50
3
0
100
4.8
100
4
1
010
8.9
100
2
2
001
6.5
50
2
2
001
4.2
80
2
1
010
6.2
75
3
1
010
7.4
65
4
0
100
6.0
90
3
0
100
7.6
100
4
1
010
9.3
50
3
0
100
4.8
100
4
1
010
8.9
100
2
2
001
6.5
importnumpy as npfrom sklearn.feature_extraction importDictVectorizerfrom sklearn importlinear_model#定义数据集
x = np.array([[100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9],
[100,2,2,6.5],[50,2,2,4.2],[80,2,1,6.2],
[75,3,1,7.4],[65,4,0,6],[90,3,0,7.6],
[100,4,1,9.3],[50,3,0,4.8],[100,4,1,8.9],[100,2,2,6.5]])
x_trans=[]for i inrange(len(x)):
x_trans.append({'x1':str(x[i][2])})
vec=DictVectorizer()
dummyX=vec.fit_transform(x_trans).toarray()
x= np.concatenate((x[:,:-2],dummyX[:,:],x[:,-1].reshape(len(x),1)),axis=1)
x=x.astype(float)
X= x[:,:-1]
Y= x[:,-1]print(x,X,Y)#训练数据
regr =linear_model.LinearRegression()
regr.fit(X,Y)print('coefficients(b1,b2...):',regr.coef_)print('intercept(b0):',regr.intercept_)






)

)





life...)




