机器学习导论 与数学分析

文章目录

  • 机器学习
    • 定义
      • 说人话
      • 例子
        • 专家系统 定义好， 应招，速度快
        • 机器学习 实验 奖惩 调参
    • 对象
      • 任务 TASK T
        • 一个或多个
      • 经验 EXPERIENCE
      • 性能PERFORMANCE
    • 类比
      • 人类学习
        • 监督学习
        • 半监督学习
        • 无监督学习
        • 增强学习
    • 可解决问题
      • 不可解决问题
      • 举例
        • f（x，y）线性模型
        • 损失函数：L最小，损失最小
      • 方式
        • 建模
          • 预测
        • 流程
        • python执行
    • 模型
      • 线性回归
      • EM模型
      • GMM图像
        • 卷积
      • SVM
      • 其他内容
    • 文献
  • 数学分析
    • 引出
      • 对函数上升速度思考
        • 分析
        • 附录
        • 总结
    • 导数
      • 常用导数
        • 应用
          • 代码
          • 图像
          • 方法
        • 应用2
          • 思想
      • 原因：梯度下降方法
    • 方向导数
      • 推导
        • 梯度
    • Taylor Maclaurin 公式
      • 应用：求e的x次方，x=0
        • e的x次方 代码
        • e的x次方 图像
        • sinx 代码和图像
      • 应用2
      • 应用3
    • gama函数
    • 凸函数
      • 特点
        • 一阶可微
        • 二阶可微
          • 海瑟矩阵
      • 举例
    • 概率论
      • 古典概型
        • 组合数
          • 熵

机器学习

定义

对于某给定任务T,在合理的性能度量方案P的前提下，某计算机程序可以自主学习任务T的经验E，随着提供合适，优质，大量经验E,该程序对于任务T性能逐步提高。

说人话

机器学习是人工智能的一个分支，我们使用计算机设计一个系统，使它能够根据提供的训练数据按照一定方式来学习，随着训练次数增加，该系统可以在性能上不断学习和改进，通过参数优化的学习模型，能够用于预测相关问题输出

例子

无人驾驶汽车

专家系统 定义好， 应招，速度快

机器学习 实验 奖惩 调参

对象

任务 TASK T

一个或多个

经验 EXPERIENCE

性能PERFORMANCE

类比

人类学习

监督学习

看月亮

半监督学习

LPA

无监督学习

阅兵 聚类

增强学习

走路 踢球

可解决问题

  1. 数据清洗/特征选择
  2. 确定算法模型/参数优化
  3. 结果预测

不可解决问题

1 大数据存储/并行运算
2 做一个机器人

举例

机器学习：“盯住二号位，她容易起快球‘
传统算法：排球规则

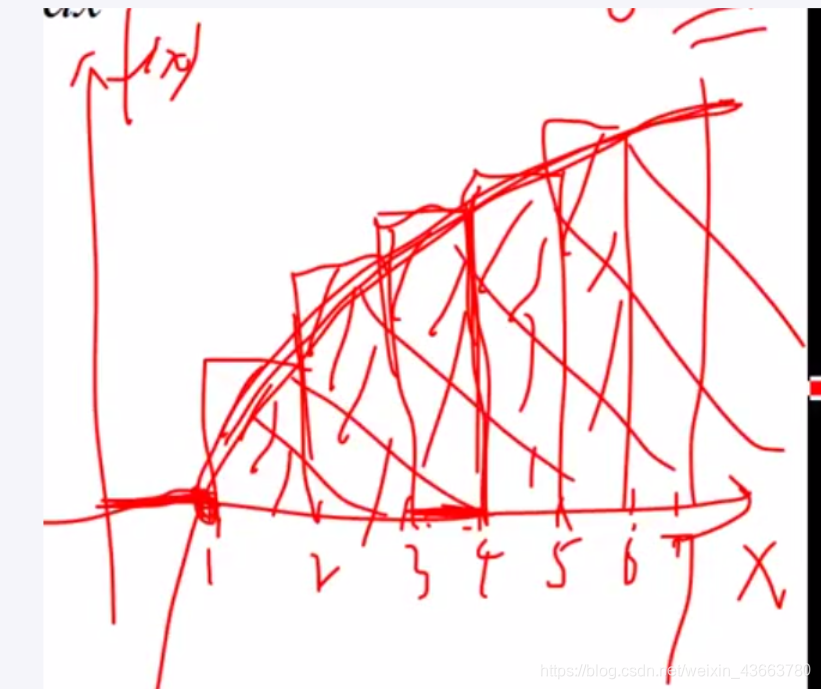
f（x，y）线性模型

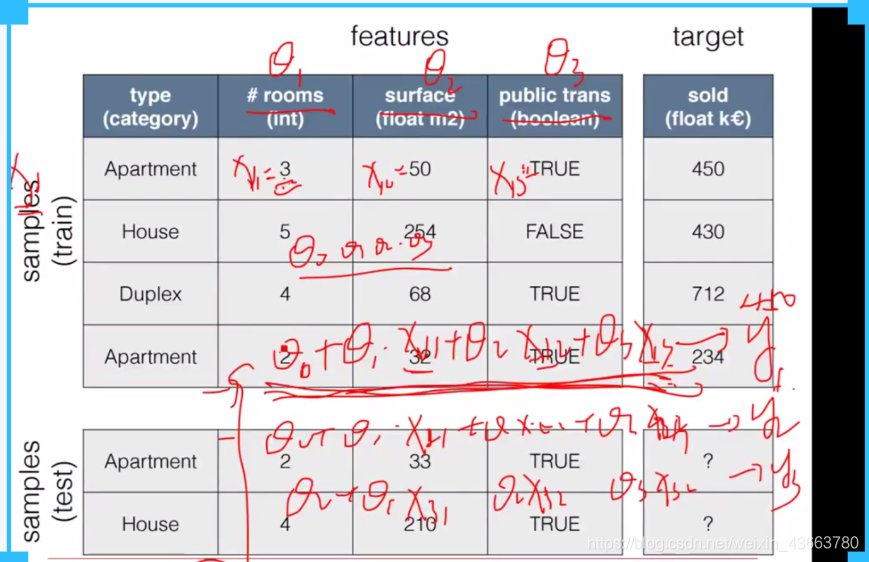
在这里插入图片描述

损失函数：L最小，损失最小

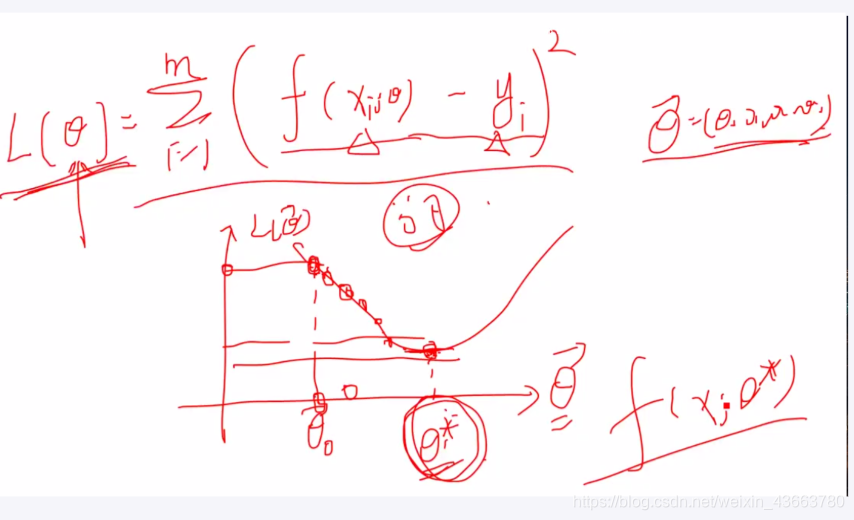
在这里插入图片描述

方式

建模

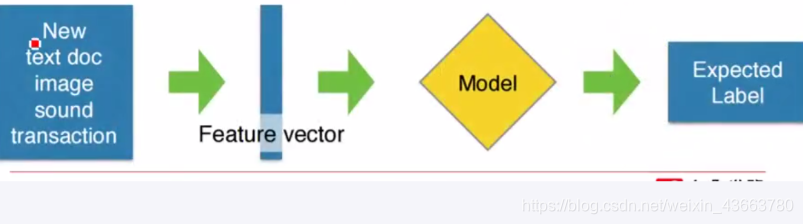
在这里插入图片描述

预测

在这里插入图片描述

流程

在这里插入图片描述

python执行

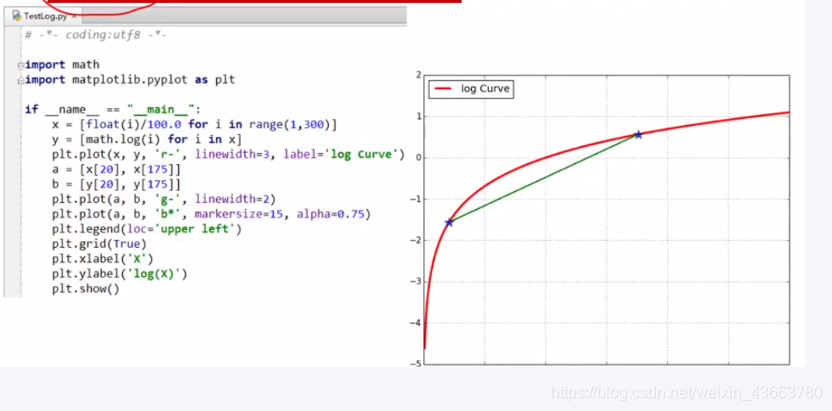
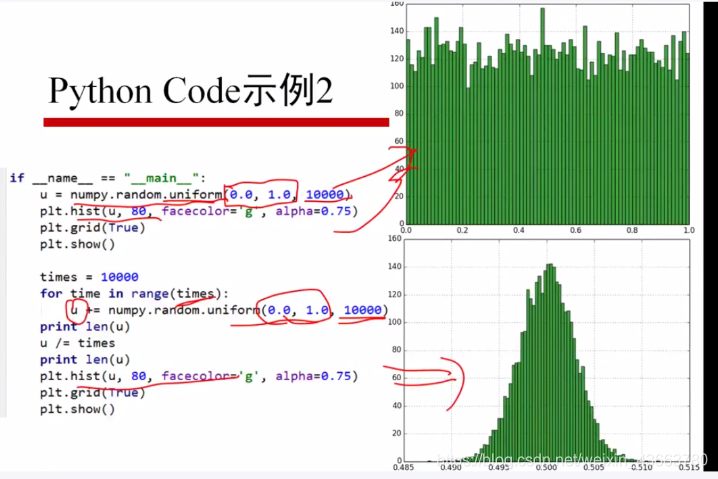
在这里插入图片描述
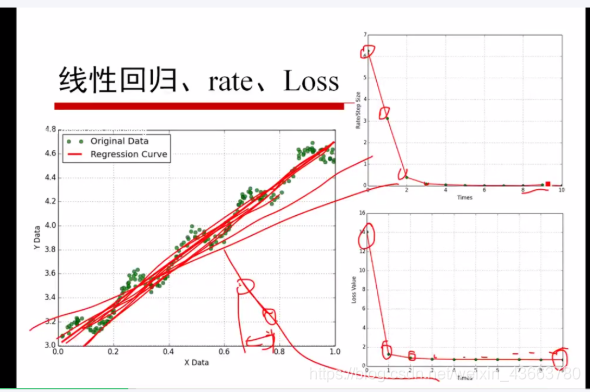
在这里插入图片描述

模型

线性回归

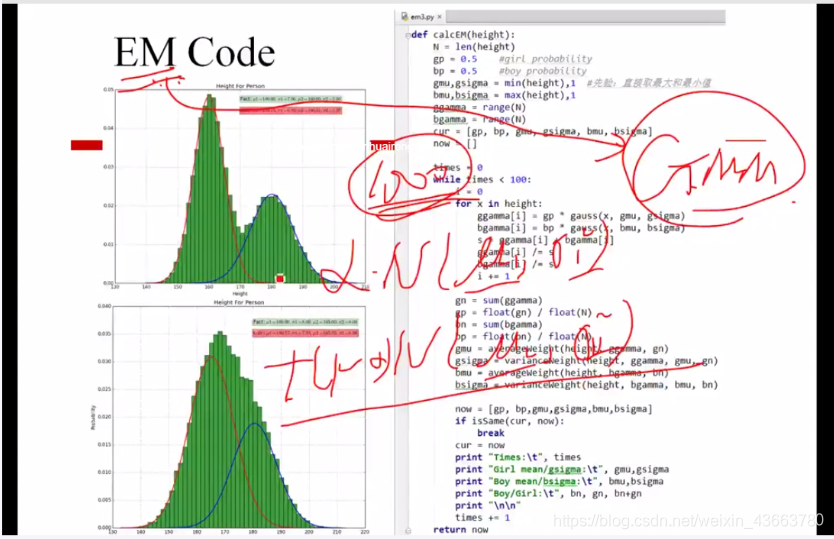
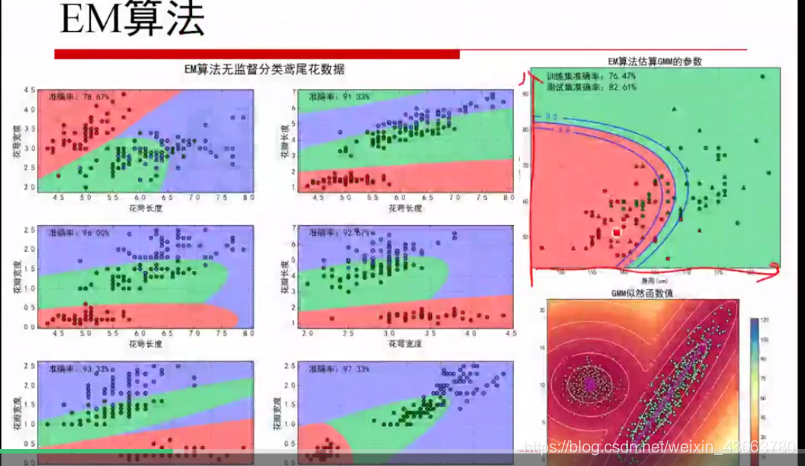
在这里插入图片描述

EM模型

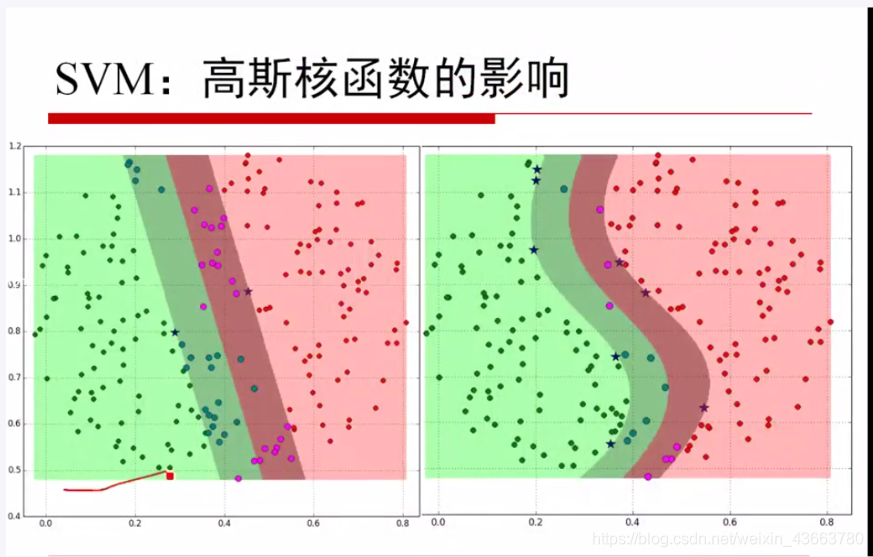
在这里插入图片描述
在这里插入图片描述

GMM图像

![在这里插入图片描述](https://img-blog.csdnimg.cn/20200403185751562.png?x-oss-process=image/watermark,type_ZmFuZ3poZW5naGVpdGk,shadow_10,text_aHR0cHM6Ly9ibG9nLmNzZG4ubmV0L3dlaXhpbl80MzY2Mzc4MA==,size_16,color_FFFFFF,t_70在这里插入图片描述

卷积

在这里插入图片描述

SVM

在这里插入图片描述

其他内容

在这里插入图片描述

文献

在这里插入图片描述

数学分析

引出

对函数上升速度思考

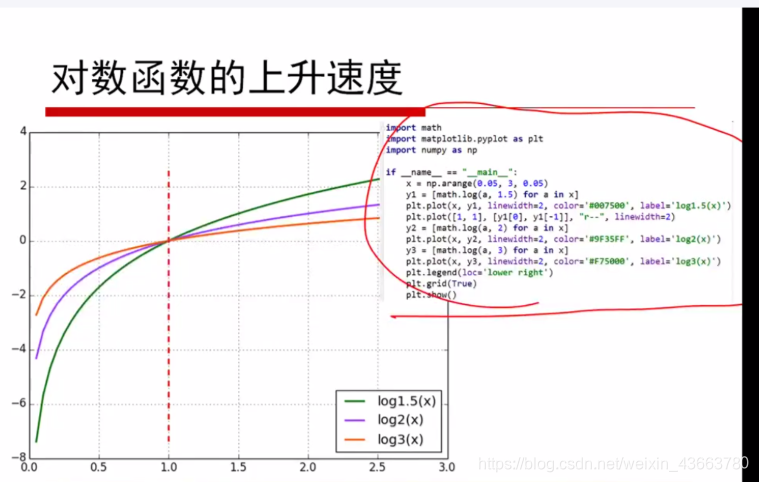
在这里插入图片描述

分析

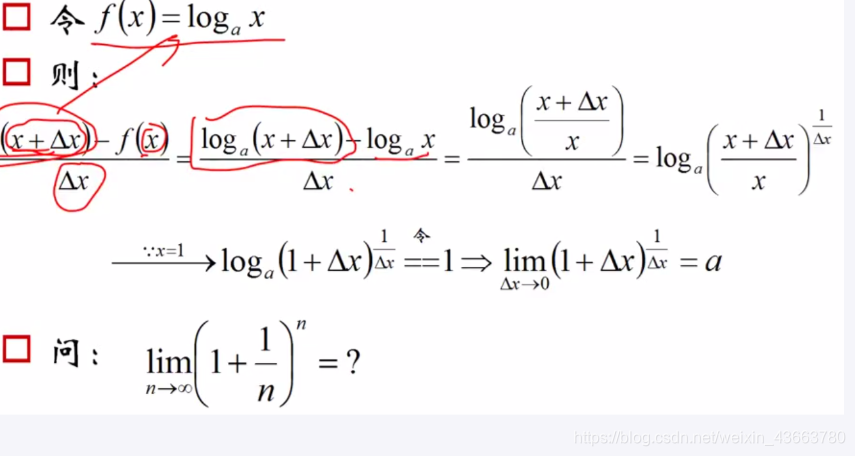
在这里插入图片描述

附录

在这里插入图片描述

总结

在这里插入图片描述

导数

  1. 简单来说，导数就是曲线斜率，是曲线变化快慢的反应

  2. 二阶导数是斜率变化快慢的反应，表征曲线凸凹性
    2.1二阶导数是连续曲线，往往称之为”***光顺***的“
    2，2加速度方向总是指向轨迹曲线凹的一侧

  3. List item

常用导数

在这里插入图片描述

应用

领会幂指函数一般处理套路
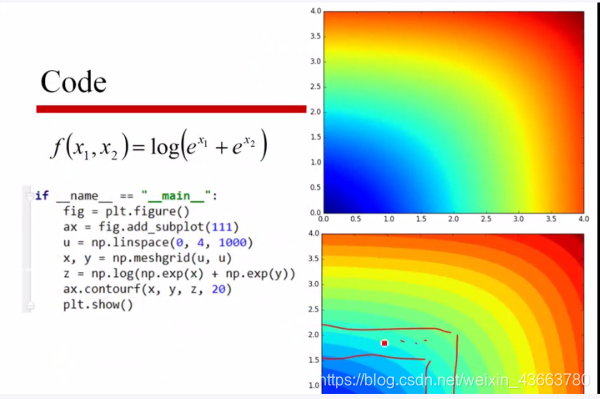
在这里插入图片描述

代码

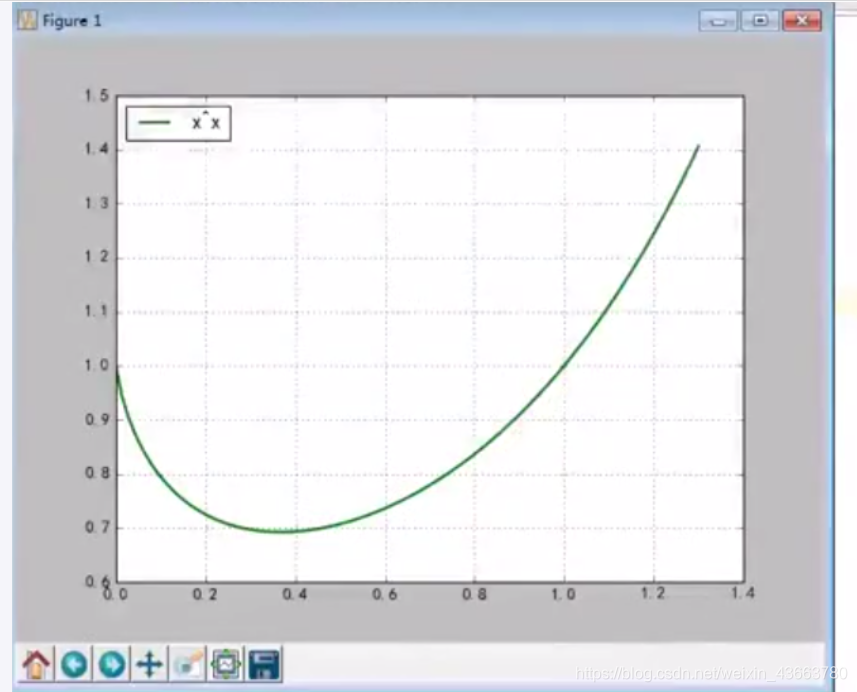
在这里插入图片描述

图像

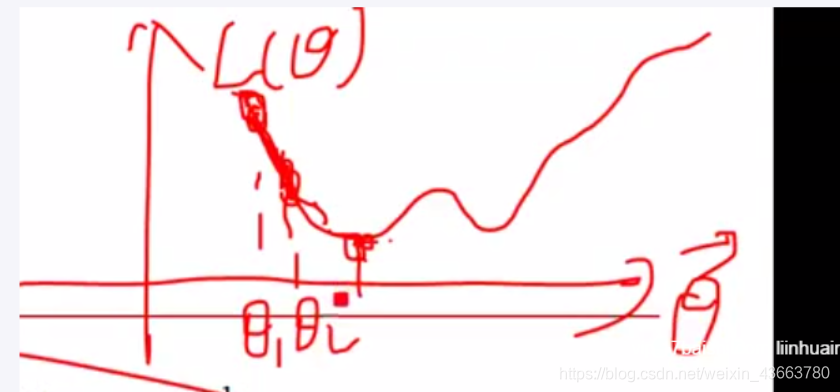
在这里插入图片描述

方法

在这里插入图片描述

应用2

在这里插入图片描述

思想

先假设
在这里插入图片描述

原因：梯度下降方法

在这里插入图片描述

方向导数

如果函数Z=f（x，y）在点P（x，y）是可微分，那么，函数在该点沿任一L方向导数都存在，且有：
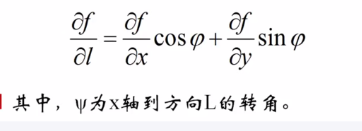
在这里插入图片描述

推导

两个看作向量
在这里插入图片描述
在这里插入图片描述

梯度

  1. 设函数Z=f（x，y）在平面区域D内具有一阶连续偏导数，则对于每一个点P(x,y)属于D，向量

在这里插入图片描述
为函数Z=f（x，y）在点P的梯度，记作gradf（x，y）

  1. 梯度的方向是函数在该点变化最快的方向
  2. 考虑一座解析式为z=H（x，y）山，在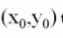在这里插入图片描述的梯度是在该点坡度变化最快方向
  3. 梯度下降法

Taylor Maclaurin 公式

在这里插入图片描述

应用：求e的x次方，x=0

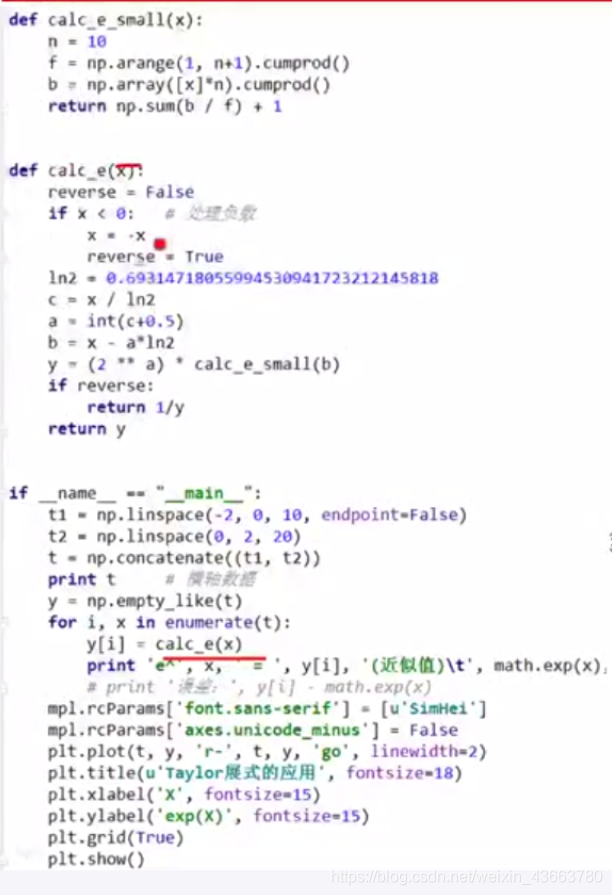
在这里插入图片描述

e的x次方 代码

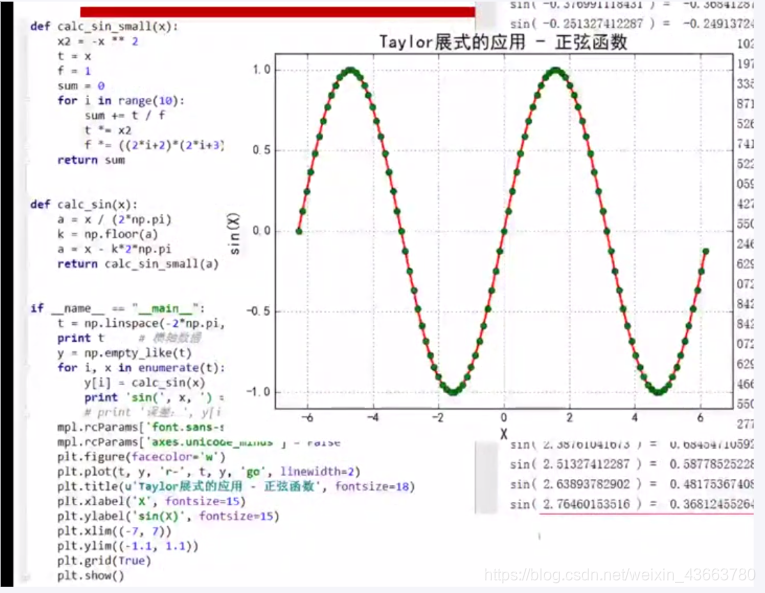
在这里插入图片描述

e的x次方 图像

在这里插入图片描述

sinx 代码和图像

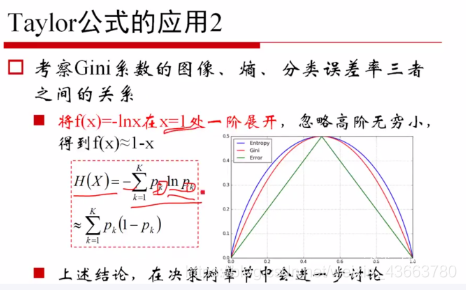
在这里插入图片描述

应用2

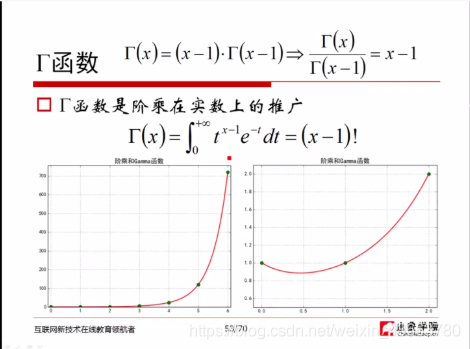
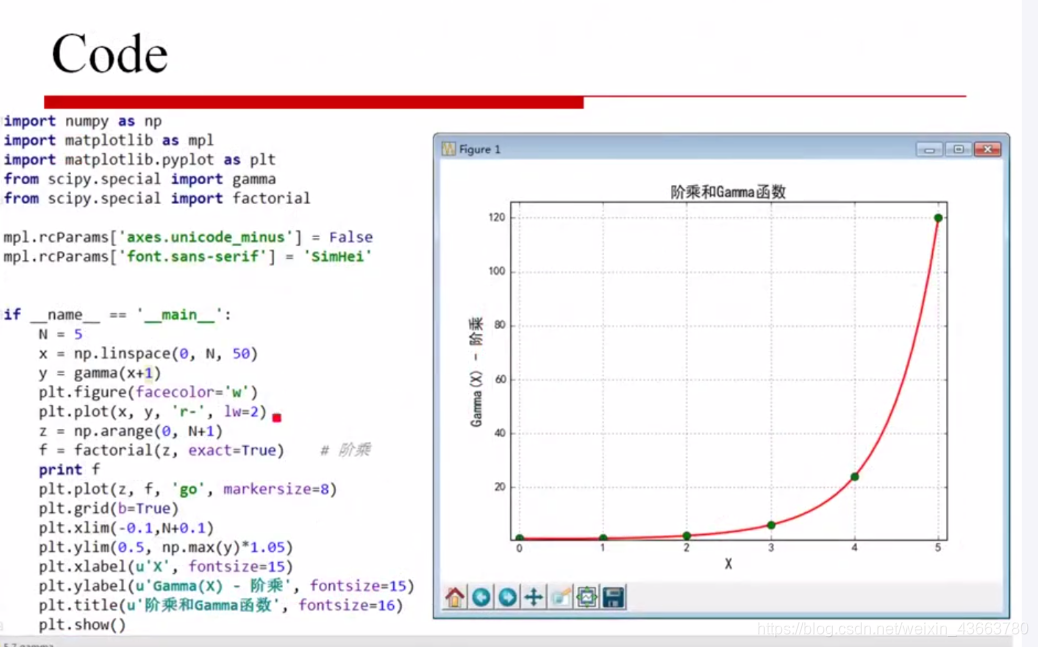
在这里插入图片描述

应用3

在这里插入图片描述
在这里插入图片描述

gama函数

在这里插入图片描述
在这里插入图片描述

凸函数

若函数f的定义域domf为凸集，且满足
在这里插入图片描述

特点

一阶可微

若f一阶可微，则函数f为凸函数当且仅当f定义域domf为凸集，且
在这里插入图片描述

二阶可微

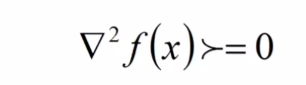
  1. 若函数f二阶可微，则函数f为凸函数当且仅当dom为凸集，且在这里插入图片描述
  2. 若f是一元函数，上式表示二阶导大于等于0
  3. 若f是多元函数，上式表示二阶导海瑟矩阵半正定
海瑟矩阵

在这里插入图片描述
4>0,23>0正定为凸函数

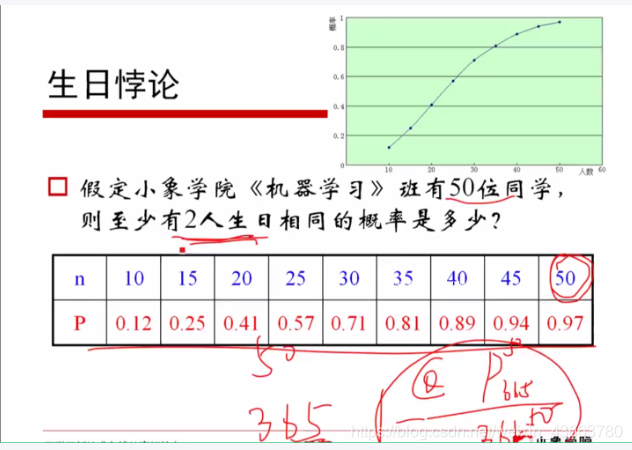
举例

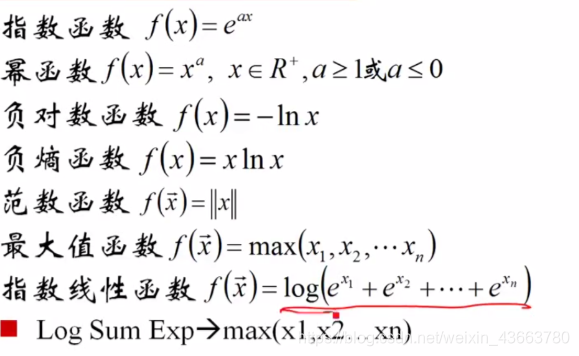
在这里插入图片描述
在这里插入图片描述

概率论

在这里插入图片描述

古典概型

在这里插入图片描述
在这里插入图片描述
在这里插入图片描述
解：

  1. 将15件产品装入3个箱子，每箱装5件，共有15！/（5！5！5！）
  2. 先把三件次品放入三个箱子，共有3！种装法。对于这样的每一种装法，把其余12件产品放入3个箱子，每箱装4件，共有12！（4！4！4！）种装法
  3. P（A）=（3*12！（4！4！4！））/（15！/（5！5！5！））=25/91

组合数

在这里插入图片描述

熵

在这里插入图片描述

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/467826.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

聊聊、Highcharts 动态数据

聊聊、Highcharts 动态数据

最近项目中需要用到图表，找了几个开源框架，最后选择 Highcharts，原因是 Highcharts 功能强大，稳定，方便，而且开源，社区比较成熟。 首先下载 Highcharts，导入项目。 在 HTML 页面引入…
阅读更多...
你知道用git打补丁吗？

你知道用git打补丁吗？

#常规操作一个常规的使用git 生成补丁的方式git diff ./ > xxx.patch patch -p1 < xxx.patch但是这样生成的补丁有一个问题&#xff0c;这个是差分形式的diff --git a/kernel-4.4/drivers/input/touchscreen/goodix.c b/kernel-4.4/drivers/input/touchscreen/goodix.c i…
阅读更多...
概率论与贝叶斯先验

概率论与贝叶斯先验

文章目录概率论与贝叶斯先验概率论基础问题代码图像本福特定律应用&#xff1a;公路堵车模型代码模型初速不同&#xff1a;影响不大减速概率&#xff1a;影响大应用&#xff1a;商品推荐解答概率公式应用样本贝叶斯公式分布两点分布二项分布泊松分布期望和方差表示强度应用均匀…
阅读更多...
vue项目导入外部css样式和js文件

vue项目导入外部css样式和js文件

转自&#xff1a;http://blog.csdn.net/xiejunna/article/details/54943957 css文件放入static文件夹下。 转载于:https://www.cnblogs.com/ourLifes/p/7444074.html
阅读更多...
Linux内核0.12完全注释

Linux内核0.12完全注释

推荐一本书 Linux 0.12内核完全注释 先把麻雀解剖了&#xff0c;再去研究老鹰和飞机可能会更好。现在市面的很多书籍都是基于比较新的内核讲解的&#xff0c;2.6的内核或者4.4的内核&#xff0c;因为内核版本越高&#xff0c;里面的东西就越多&#xff0c;想要讲解明白就需要花…
阅读更多...
矩阵和线性代数

矩阵和线性代数

文章目录矩阵和线性代数矩阵SVD提法举例推导代码分解效果方阵行列式范德蒙行列式作用代数余子式伴随矩阵方阵的逆矩阵乘法模型举例概率转移矩阵平稳分布&#xff1a;向量乘法矩阵的秩秩与方程组的解推论向量组等价系数矩阵对CAB重认识正交阵特征值和特征向量性质不同特征值对应…
阅读更多...
对比一段ADC键值读取的代码

对比一段ADC键值读取的代码

最近接触到的一个代码&#xff0c;这个代码看起来很简单&#xff0c;但是却蕴藏了人类的智慧与结晶。正是这些不断产生的智慧与结晶&#xff0c;让我们的电子产品越来越稳定&#xff0c;越来越智能。周五了&#xff0c;评论文章&#xff0c;选两个同学赠送书籍《Linux内核完全剖…
阅读更多...
HTML5权威指南 11.通信API

HTML5权威指南 11.通信API

1 <!DOCTYPE html>2 <html>3 4 <head>5 <meta charset"UTF-8">6 <title></title>7 <script type"text/javascript">8 //&#xff08;1&#xff09;监听message事件9 window.addEve…
阅读更多...
在线登记系统代码 php_PHP框架实现WebSocket在线聊天通讯系统

在线登记系统代码 php_PHP框架实现WebSocket在线聊天通讯系统

ThinkPHP使用Swoole需要安装think-swooleComposer包&#xff0c;前提系统已经安装好了SwoolePECL拓展tp5的项目根目录下执行composer命令安装think-swoole&#xff1a;composerrequiretopthink/think-swoole话不多说&#xff0c;直接上代码&#xff1a;新建WebSocket.php控制器…
阅读更多...
机器学习数据包之numpy

机器学习数据包之numpy

numpy 属性 import numpy as np#矩阵运算arraynp.array([[1,2,3],[2,3,4]])print (array)[[1 2 3][2 3 4]]维度 print(number of dim,array.ndim)number of dim 2形状 print(shape,array.shape)shape (2, 3)大小 print(size,array.size)size 6创建 创建类型 anp.array([…
阅读更多...
RK 利用SARADC 来做多个按键

RK 利用SARADC 来做多个按键

#DTS配置#配置DTS节点#驱动文件中匹配 DTS 节点#驱动说明#获取ADC通道#获取ADC值#计算采集到的电压#接口说明#调试方法#节点ADC值RK3399开发板上的 AD 接口有两种&#xff0c;分别为&#xff1a;温度传感器 (Temperature Sensor)、逐次逼近ADC (Successive Approximation Regis…
阅读更多...
概率论之pandas

概率论之pandas

快速入门 1 import numpy as npspd.series([1,3,5,np.nan,8,4])Series spd.Series([1,3,5,np.nan,8,4])sOut[6]: 0 1.01 3.02 5.03 NaN4 8.05 4.0dtype: float64date_range datespd.date_range(20190301,periods6)datesOut[10]: DatetimeIndex([2019-03-…
阅读更多...
学习，一定是脱“贫”致富的捷径

学习，一定是脱“贫”致富的捷径

周末加班&#xff0c;加班后觉得有点无聊&#xff0c;到公司阳台坐了坐&#xff0c;想到最近的工作和生活&#xff0c;也理了理最近的状态&#xff0c;然后分享了一段话在知识星球里。如下:我平时很少静下来想东西&#xff0c;其中一个原因是因为我害怕安静&#xff0c;晚上睡觉…
阅读更多...
人应该活成什么样子？该以什么方式活着？

人应该活成什么样子？该以什么方式活着？

“您幸福吗&#xff1f;”“我是外地打工的&#xff0c;不要问我。”“您幸福吗&#xff1f;”“我姓曾。”相信大家还记得这段央视走基层采访的经典问答。“幸福是什么”是一个人类社会中被广泛讨论的话题&#xff0c;人要怎么生活才能获得幸福&#xff0c;一直是众生要追寻的…
阅读更多...
MIPI白皮书

MIPI白皮书

#mipi 5G中优势#5G手机中的mipi#mipi#背景2020年 是5G元年&#xff0c;很多行业因5g重新定义。显示行业也不例外&#xff0c;针对5G&#xff0c;mipi联盟发表了对应的白皮书 描述了现有的MIPI规范如何能够支持第一代5G智能手机以及其他新兴的5G移动平台&#xff0c;包括互联/自…
阅读更多...
redis rdb aof区别_Redis 持久化之 RDB 与 AOF 详解

redis rdb aof区别_Redis 持久化之 RDB 与 AOF 详解

走过路过不要错过点击蓝字关注我们文章出处&#xff1a;https://www.cnblogs.com/jojop/p/13941195.htmlRedis 持久化我们知道Redis的数据是全部存储在内存中的&#xff0c;如果机器突然GG&#xff0c;那么数据就会全部丢失&#xff0c;因此需要有持久化机制来保证数据不会因为…
阅读更多...
块设备驱动初探

块设备驱动初探

前言研究IO也很久了&#xff0c;一直无法串联bio和块设备驱动&#xff0c;只知道bio经过IO调度算法传递到块设备驱动&#xff0c;怎么过去的&#xff0c;IO调度算法在哪里发挥作用&#xff0c;一直没有完全搞明白&#xff0c;查看了很多资料&#xff0c;终于对块设备驱动有所理…
阅读更多...
Linux 块设备，Block Layer层架构演变

Linux 块设备，Block Layer层架构演变

前言Block Layer层在整个I/O中负责承上启下&#xff0c;上接文件系统&#xff0c;下接块驱动。我不想直接讨论代码&#xff0c;希望从一个架构的演变来初探一下Block Layer层。一、1.0版本首先我们来了解几个重要的数据结构1.1 biobio代表了一次I/0请求&#xff0c;代表一个块设…
阅读更多...
matalotlib（2）

matalotlib（2）

文章目录注释文字Tex公式区域填充极坐标注释 import matplotlib.pyplot as plt import numpy as np xnp.arange(-10,11,1) yx*x plt.plot(x,y)plt.annotate(this is the bottom,xy(0,1),xytext(0,20),arrowpropsdict(facecolorr,frac0.2)) plt.show()文字 import matplotlib…
阅读更多...
去华为吗？

去华为吗？

昨晚的这条朋友圈很多人给我回复&#xff0c;支持去华为的人很多&#xff0c;但是也有几个反对的&#xff0c;一个说&#xff0c;怕是有命赚钱&#xff0c;没命花钱吧。还有一个说&#xff0c;自己拿到了华为offer&#xff0c;但是拒绝了&#xff0c;去了一个做开关电源的公司做…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023