一致性Hash算法

关于一致性Hash算法，在我之前的博文中已经有多次提到了，MemCache超详细解读一文中”一致性Hash算法”部分，对于为什么要使用一致性Hash算法、一致性Hash算法的算法原理做了详细的解读。

算法的具体原理这里再次贴上：

先构造一个长度为2^32的整数环(这个环被称为一致性Hash环)，根据节点名称的Hash值(其分布为[0, 2^32-1])将服务器节点放置在这个Hash环上，然后根据数据的Key值计算得到其Hash值(其分布也为[0, 2^32-1])，接着在Hash环上顺时针查找距离这个Key值的Hash值最近的服务器节点，完成Key到服务器的映射查找。

这种算法解决了普通余数Hash算法伸缩性差的问题，可以保证在上线、下线服务器的情况下尽量有多的请求命中原来路由到的服务器。

当然，万事不可能十全十美，一致性Hash算法比普通的余数Hash算法更具有伸缩性，但是同时其算法实现也更为复杂，本文就来研究一下，如何利用Java代码实现一致性Hash算法。在开始之前，先对一致性Hash算法中的几个核心问题进行一些探究。

数据结构的选取

一致性Hash算法最先要考虑的一个问题是：构造出一个长度为2^32的整数环，根据节点名称的Hash值将服务器节点放置在这个Hash环上。

那么，整数环应该使用何种数据结构，才能使得运行时的时间复杂度最低？首先说明一点，关于时间复杂度，常见的时间复杂度与时间效率的关系有如下的经验规则：

O(1) < O(log2N) < O(n) < O(N * logN) < O(N^2) < O(N^3) < 2^N < 3^N < N!

一般来说，前四个效率比较高，中间两个差强人意，后三个比较差(只要N比较大，这个算法就动不了了)。OK，继续前面的话题，应该如何选取数据结构，我认为有以下几种可行的解决方案。

1、解决方案一：排序+List

我想到的第一种思路是：算出所有待加入数据结构的节点名称的Hash值放入一个数组中，然后使用某种排序算法将其从小到大进行排序，最后将排序后的数据放入List中，采用List而不是数组是为了结点的扩展考虑。

之后，待路由的结点，只需要在List中找到第一个Hash值比它大的服务器节点就可以了，比如服务器节点的Hash值是[0,2,4,6,8,10]，带路由的结点是7，只需要找到第一个比7大的整数，也就是8，就是我们最终需要路由过去的服务器节点。

如果暂时不考虑前面的排序，那么这种解决方案的时间复杂度：

(1)最好的情况是第一次就找到，时间复杂度为O(1)

(2)最坏的情况是最后一次才找到，时间复杂度为O(N)

平均下来时间复杂度为O(0.5N+0.5)，忽略首项系数和常数，时间复杂度为O(N)。

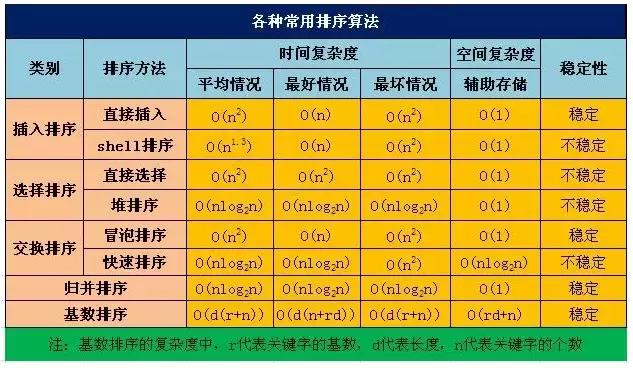
但是如果考虑到之前的排序，我在网上找了张图，提供了各种排序算法的时间复杂度：

2、解决方案二：遍历+List

既然排序操作比较耗性能，那么能不能不排序？可以的，所以进一步的，有了第二种解决方案。

解决方案使用List不变，不过可以采用遍历的方式：

(1)服务器节点不排序，其Hash值全部直接放入一个List中

(2)带路由的节点，算出其Hash值，由于指明了”顺时针”，因此遍历List，比待路由的节点Hash值大的算出差值并记录，比待路由节点Hash值小的忽略

(3)算出所有的差值之后，最小的那个，就是最终需要路由过去的节点

在这个算法中，看一下时间复杂度：

1、最好情况是只有一个服务器节点的Hash值大于带路由结点的Hash值，其时间复杂度是O(N)+O(1)=O(N+1)，忽略常数项，即O(N)

2、最坏情况是所有服务器节点的Hash值都大于带路由结点的Hash值，其时间复杂度是O(N)+O(N)=O(2N)，忽略首项系数，即O(N)

所以，总的时间复杂度就是O(N)。其实算法还能更改进一些：给一个位置变量X，如果新的差值比原差值小，X替换为新的位置，否则X不变。这样遍历就减少了一轮，不过经过改进后的算法时间复杂度仍为O(N)。

总而言之，这个解决方案和解决方案一相比，总体来看，似乎更好了一些。

3、解决方案三：二叉查找树

抛开List这种数据结构，另一种数据结构则是使用二叉查找树。

当然我们不能简单地使用二叉查找树，因为可能出现不平衡的情况。平衡二叉查找树有AVL树、红黑树等，这里使用红黑树，选用红黑树的原因有两点：

1、红黑树主要的作用是用于存储有序的数据，这其实和第一种解决方案的思路又不谋而合了，但是它的效率非常高

2、JDK里面提供了红黑树的代码实现TreeMap和TreeSet

另外，以TreeMap为例，TreeMap本身提供了一个tailMap(K fromKey)方法，支持从红黑树中查找比fromKey大的值的集合，但并不需要遍历整个数据结构。

使用红黑树，可以使得查找的时间复杂度降低为O(logN)，比上面两种解决方案，效率大大提升。

为了验证这个说法，我做了一次测试，从大量数据中查找第一个大于其中间值的那个数据，比如10000数据就找第一个大于5000的数据(模拟平均的情况)。看一下O(N)时间复杂度和O(logN)时间复杂度运行效率的对比：

因为再大就内存溢出了，所以只测试到4000000数据。可以看到，数据查找的效率，TreeMap是完胜的，其实再增大数据测试也是一样的，红黑树的数据结构决定了任何一个大于N的最小数据，它都只需要几次至几十次查找就可以查到。

当然，明确一点，有利必有弊，根据我另外一次测试得到的结论是，为了维护红黑树，数据插入效率TreeMap在三种数据结构里面是最差的，且插入要慢上5~10倍。

Hash值重新计算

服务器节点我们肯定用字符串来表示，比如”192.168.1.1″、”192.168.1.2″，根据字符串得到其Hash值，那么另外一个重要的问题就是Hash值要重新计算，这个问题是我在测试String的hashCode()方法的时候发现的，不妨来看一下为什么要重新计算Hash值：

/*** String的hashCode()方法运算结果查看* @author 哓哓**/public class StringHashCodeTest { public static void main(String[] args) { System.out.println("192.168.0.0:111的哈希值：" + "192.168.0.0:1111".hashCode()); System.out.println("192.168.0.1:111的哈希值：" + "192.168.0.1:1111".hashCode()); System.out.println("192.168.0.2:111的哈希值：" + "192.168.0.2:1111".hashCode()); System.out.println("192.168.0.3:111的哈希值：" + "192.168.0.3:1111".hashCode()); System.out.println("192.168.0.4:111的哈希值：" + "192.168.0.4:1111".hashCode()); }}

我们在做集群的时候，集群点的IP以这种连续的形式存在是很正常的。看一下运行结果为：

192.168.0.0:111的哈希值：1845870087192.168.0.1:111的哈希值：1874499238192.168.0.2:111的哈希值：1903128389192.168.0.3:111的哈希值：1931757540192.168.0.4:111的哈希值：1960386691

这个就问题大了，[0,2^32-1]的区间之中，5个HashCode值却只分布在这么小小的一个区间，什么概念？[0,2^32-1]中有4294967296个数字，而我们的区间只有122516605，从概率学上讲这将导致97%待路由的服务器都被路由到”192.168.0.1″这个集群点上，简直是糟糕透了！

另外还有一个不好的地方：规定的区间是非负数，String的hashCode()方法却会产生负数(不信用”192.168.1.0:1111″试试看就知道了)。不过这个问题好解决，取绝对值就是一种解决的办法。

综上，String重写的hashCode()方法在一致性Hash算法中没有任何实用价值，得找个算法重新计算HashCode。这种重新计算Hash值的算法有很多，比如CRC32_HASH、FNV1_32_HASH、KETAMA_HASH等，其中KETAMA_HASH是默认的MemCache推荐的一致性Hash算法，用别的Hash算法也可以，比如FNV1_32_HASH算法的计算效率就会高一些。

一致性Hash算法实现版本1：不带虚拟节点

使用一致性Hash算法，尽管增强了系统的伸缩性，但是也有可能导致负载分布不均匀，解决办法就是使用虚拟节点代替真实节点，第一个代码版本，先来个简单的，不带虚拟节点。

下面来看一下不带虚拟节点的一致性Hash算法的Java代码实现：

/** * 不带虚拟结点的一致性Hash算法 * @author 哓哓 * */public class ConsistentHashWithoutVN {​ /** * 待加入Hash环的服务器列表 */ private static String[] servers = { "192.168.0.0:111