逻辑回归本质是分类问题，而且是二分类问题，不属于回归，但是为什么又叫回归呢。我们可以这样理解，逻辑回归就是用回归的办法来做分类。它是在线性回归的基础上，通过Sigmoid函数进行了非线性转换，从而具有更强的拟合能力

sigmoid 函数

https://blog.csdn.net/fenglepeng/article/details/104829873

Logistic回归分类器

为了实现Logistic回归分类器，我们可以在每个特征上都乘以一个回归系数，然后把所有的结果值相加，将这个总和代入Sigmoid函数中，进而得到一个范围在0~1之间的数值。任何大于0.5的数据被分入1类，小于0.5即被归入0类。所以，Logistic回归也可以被看成是一种概率估计。

$\begin{aligned}p&=h_\theta(x)=g(\theta^Tx)=\frac{1}{1+e^{-\theta^Tx}} \end{aligned}$

所以说，Logistic回归分类器可以看成线性回归与sigmoid的混合函数，是一个二分类的模型（这里是取的0和1，有的算法是+1和-1）

$\hat{y}=\left\{\begin{matrix} 0,P(\hat{y}=1)>p\\ 1,P(\hat{y}=0)>p \end{matrix}\right.$

在用于分类时，实际上是找一个阈值，大于阈值的属于1类别，小于的属于0类别。（阈值是可根据具体情况进行相应变动的）

Logistic回归及似然函数

我们假设

$\begin{aligned}P(y=1|x;\theta)&=h_\theta(x) \\P(y=0|x;\theta)&=1-h_\theta(x) \end{aligned}$

把两个式子结合起来

$\begin{aligned}P(y|x;\theta)&=(h_\theta(x))^y(1-h_\theta(x))^{(1-y)}\end{aligned}$

运用极大似然估计得到似然函数

$\begin{aligned}L(\theta)&=p(\vec{y}|X;\theta) \\&=\prod_{i=1}^{m}p(y^{(i)}|x^{(i)};\theta) \\&=\prod_{i=1}^{m}(h_\theta(x^{(i)}))^{y^{(i)}}(1-h_\theta(x^{(i)}))^{(1-y^{(i)})}\end{aligned}$

累乘不好求，我们可以求其对数似然函数。最值的问题，求导（第三行到第四行使用了sigmoid函数求导）

$\begin{aligned}l(\theta)&=\log L(\theta) \\&=\sum_{i=1}^m(y^{(i)}\log h_\theta(x^{(i)})+(1-y^{(i)})\log(1-h_\theta(x^{(i)}))) \\\frac{\partial l(\theta)}{\partial\theta_j}&=\sum_{i=1}^m(\frac{y^{(i)}}{h_\theta(x^{(i)})}-\frac{1-y^{(i)}}{1-h_\theta(x^{(i)})})\cdot\frac{\partial h_\theta(x^{(i)})}{\partial\theta_j} \\&=\sum_{i=1}^m(\frac{y^{(i)}}{g(\theta^Tx^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^Tx^{(i)})})\cdot\frac{\partial g(\theta^Tx^{(i)})}{\partial\theta_j} \\&=\sum_{i=1}^m(\frac{y^{(i)}}{g(\theta^Tx^{(i)})}-\frac{1-y^{(i)}}{1-g(\theta^Tx^{(i)})})\cdot g(\theta^Tx^{(i)})(1-g(\theta^Tx^{(i)}))\cdot\frac{\partial\theta^Tx^{(i)}}{\partial\theta_j} \\&=\sum_{i=1}^m(y^{(i)}(1-g(\theta^Tx^{(i)}))-(1-y^{(i)})g(\theta^Tx^{(i)}))\cdot x_j^{(i)} \\&=\sum_{i=1}^m(y^{(i)}-g(\theta^Tx^{(i)}))\cdot x_j^{(i)}\end{aligned}$

求解，使用批量梯度下降法BGD

$\theta_j=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$

或者随机梯度下降法SGD

$\theta_j=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$

可以发现逻辑回归与线性回归梯度下降求解的形式类似，唯一的区别在于假设函数hθ(x)不同，线性回归假设函数为θTx，逻辑回归假设函数为Sigmoid函数。

线性回归模型服从正态分布，逻辑回归模型服从二项分布（Bernoulli分布），因此逻辑回归不能应用最小二乘法作为目标/损失函数，所以用梯度下降法。

极大似然估计与Logistic回归损失函数

我们要让对数似然函数最大，也就是他的相反数 $-l(\theta )$ 最小。而 $-l(\theta )$ 最小化，则可以看成损失函数，求其最小化：

$loss = -l(\theta )$

似然函数：

$\begin{aligned}L(\theta)&=\prod_{i=1}^mp(y^{(i)}|x^{(i)};\theta) =\prod_{i=1}^mp_i^{y^{(i)}}(1-p_i)^{1-y^{(i)}} \end{aligned}$

logistic函数

$\begin{aligned}p_i&=h_\theta(x^{(i)}) =\frac{1}{1+e^{-\theta^Tx^{(i)}}} \end{aligned}$

带入得

$\begin{aligned}\\l(\theta)&=\ln L(\theta) \\&=\sum_{i=1}^m\ln[p_i^{y^{(i)}}(1-p_i)^{1-y^{(i)}}] \\&=\sum_{i=1}^m\ln[(\frac{1}{1+e^{-f_i}})^{y^{(i)}}(\frac{1}{1+e^{f_i}})^{1-y^{(i)}}] \\loss(y^{(i)},\hat{y^{(i)}})&=-l(\theta) \\&=\sum_{i=1}^m[y^{(i)}\ln(1+e^{-f_i})+(1-y^{(i)})\ln(1+e^{f_i})] \\&=\begin{cases}\sum_{i=1}^m\ln(1+e^{-f_i}), &y^{(i)}=1 \\ \sum_{i=1}^m\ln(1+e^{f_i}), &y^{(i)}=0\end{cases} \\\Rightarrow loss(y^{(i)},\hat{y^{(i)}})&=\sum_{i=1}^m\ln(1+e^{(1-2y^{(i)})\theta^Tx^{(i)}}), y^{(i)}=\begin{cases}1 \\ 0\end{cases}\end{aligned}$

这个结果就是交叉熵损失函数。

总结

就一句话：通过以上过程，会发现逻辑回归的求解，跟线性回归的求解基本相同。

多分类问题（Multi-class classification）

对于分类多于2个的问题，可以将其看做二分类问题，即以其中一个分类作为一类，剩下的其他分类作为另一类，多分类问题的假设函数为

$h_{0}^{i}(x)=p(y=i|x;\theta)$

one-vs-all/rest 问题解决方法：

训练一个逻辑回归分类器，预测 i 类别 y=i 的概率；
对一个新的输入值x，为了作出类别预测，分别在k个分类器运行输入值，选择h最大的类别

Softmax回归模型

Softmax回归是logistic回归的一般化模型，适用于k（k>2）分类的问题，第k类的参数为向量 $\theta_k$ ，组成的二维矩阵为 $\theta _{k*n}$ (k为类别数，n为特征数，即为每一个类别构建一个 $\theta_k$ ，用到的是ova思想)。

参考链接：机器学习之单标签多分类及多标签多分类

Softmax函数的本质就是将一个k维的任意实数向量映射成为另一个k维的实数向量，其中向量中的每个元素的取值都介于（0,1）之间。

Softmax回归的概率函数为：

$p(y=k|x;\theta)=\frac{e^{\theta_k^Tx}}{\sum_{l=1}^{K}e^{\theta_l^{T}x}}, k=1,2,...,K$
注释： $e^{\theta_k^Tx}$ 计算的是，他属于第k类的回归值， $\sum_{l=1}^{K}e^{\theta_l^{T}x}$ 计算的是他属于每个类别的累加，用e的指数是为了加大大的类别的影响

Softmax回归的似然估计

似然函数：

$\begin{aligned}L(\theta)&=\prod_{i=1}^m\prod_{k=1}^Kp(y=k|x^{(i)};\theta)^{y_k^{(i)}} \\&=\prod_{i=1}^m\prod_{k=1}^K(\frac{e^{\theta_k^Tx}}{\sum_{l=1}^Ke^{\theta_l^Tx}})^{y_k^{(i)}}\end{aligned}$

对数似然函数：

$\begin{aligned}l(\theta)&=\ln L(\theta) \\&=\sum_{i=1}^m\sum_{k=1}^Ky_k^{(i)}(\theta_k^Tx^{(i)}-\ln\sum_{l=1}^Ke^{\theta_l^Tx^{(i)}}) \\l(\theta)&=\sum_{k=1}^Ky_k(\theta_k^Tx-\ln\sum_{l=1}^Ke^{\theta_l^Tx})\end{aligned}$

推导和Logistic回归类似，只是将分类的个数从2扩展到k的情形。Softmax算法的损失函数：

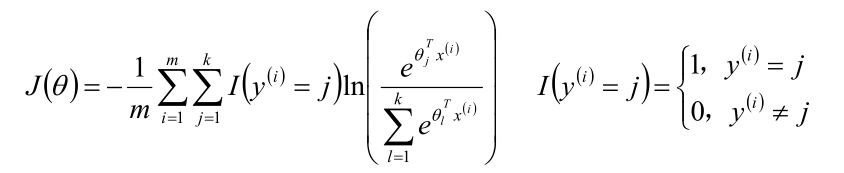
梯度下降法

总结

线性回归模型一般用于回归问题，逻辑回归和Softmax回归模型一般用于分类问题；
求θ的主要方式是梯度下降算法，该算法是参数优化的重要手段，主要使用SGD或MBGD；
逻辑回归/Softmax回归模型是实际问题中解决分类问题的最重要的方法；
广义线性模型对样本的要求不必一定要服从正态分布，只要服从指数分布簇（二项分布、Poisson分布、Bernoulli分布、指数分布等）即可；广义线性模型的自变量可以是连续的也可以是离散的。