哈夫曼编码的原理

参考文章：哈夫曼编码详解——图解真能看了秒懂

简单总结其原理：

需求：对重复出现的元素进行二进制编码，最高效的编码方式是哈夫曼编码。

方法：按照元素出现的频率大小构造一棵树，出现次数越多的元素越靠近树根，其编码长度（即比特位个数）越短。

效果：因为 编码长度 * 出现次数 = 总存储空间，所以使用哈夫曼编码，总存储空间最短。

元素出现频率，广义化，就是权值。广义化以后 ，权值可以为小数，就是一个乘数因子而已。

画法

这里取了一串小数作为权值。

需要说明的是，每次建树，从当前剩下的权值列表中取两个最小的权值，将他们之和作为根节点，此根节点代替子节点作为权值列表的一部分。

最好先对权值做一个排序，这样更容易找最小值。

步骤一

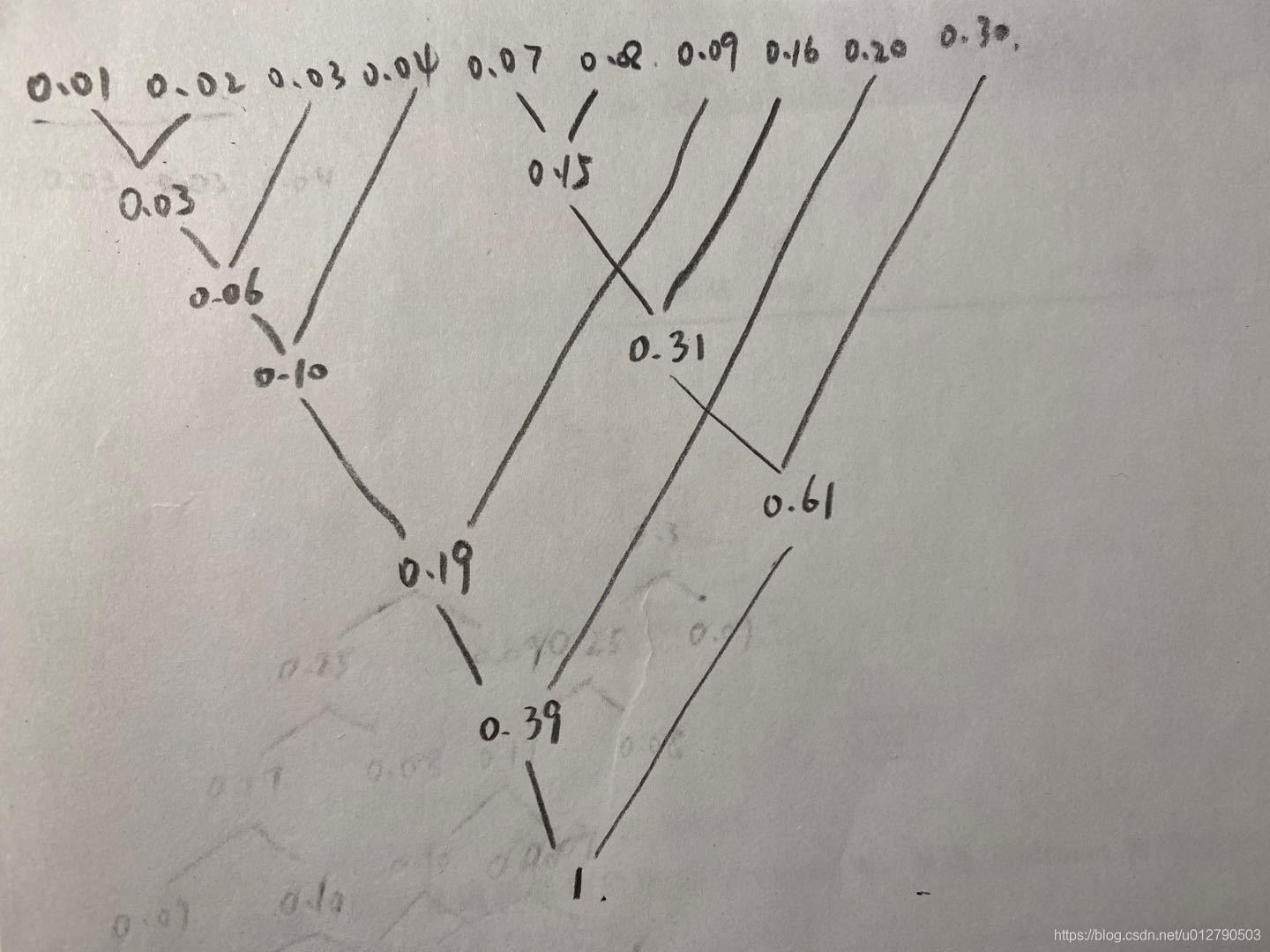
步骤二

画完以后将树倒置过来，对节点位置调整摆放即可。如下图

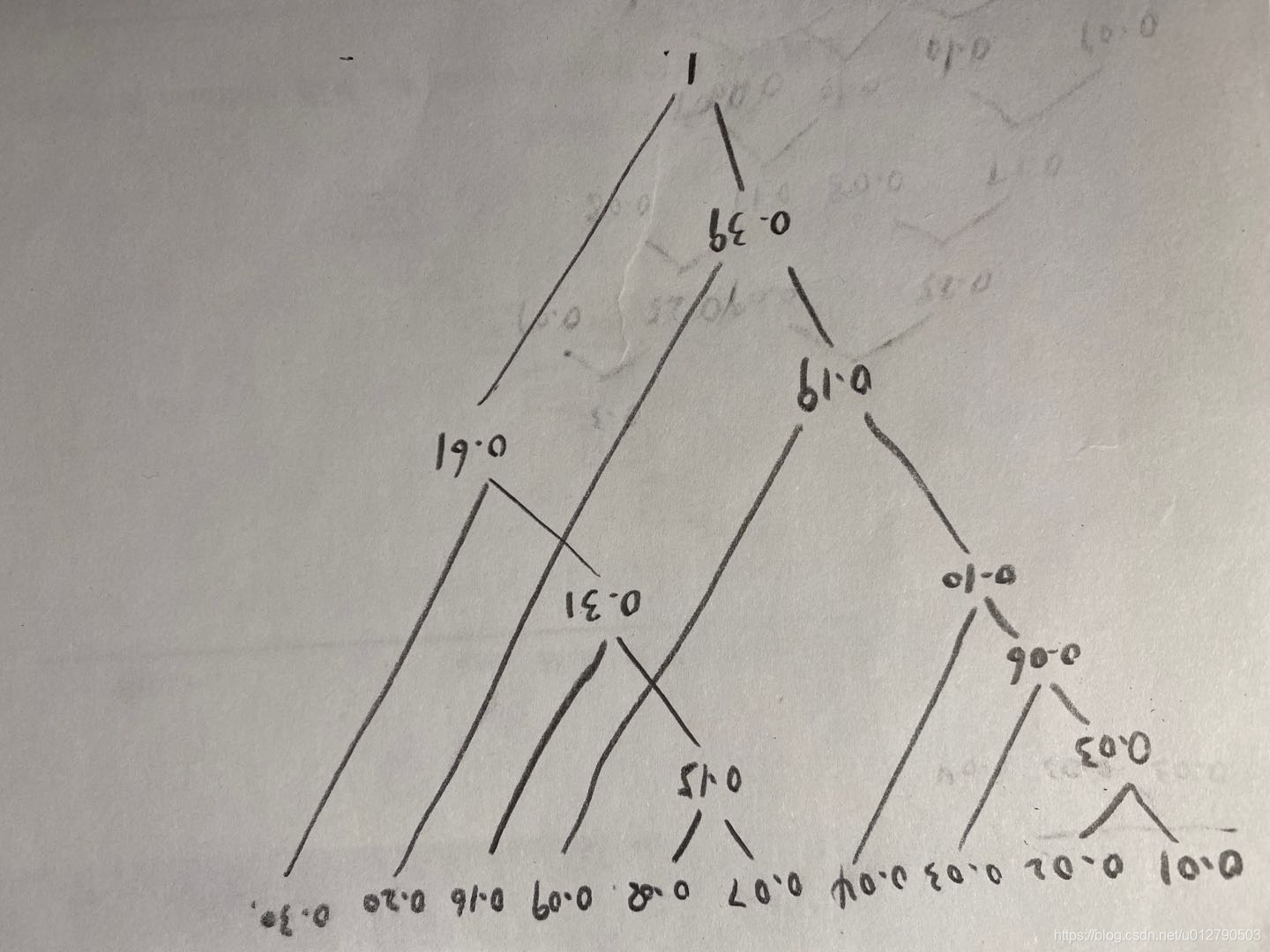
这样一来，计算上很连续，不需要产生很多中间结果，可以提高手算速度和准确度。

最后，给所有叶子节点编码：

左边的连线为0，右边的连线为1，从根节点到叶子节点的路径就是叶子节点的编码。