MATLAB中BP神经网络用于回归拟合算法实现（另附GRNN代码）

BP神经网络：是1986年由Rumelhart和McClelland为首的科学家提出的概念，是一种按照误差逆向传播算法训练的多层前馈神经网络，是目前应用最广泛的神经网络。神经网络是把生活中的常见情节推广到计算仿真的范畴，这样的启发式算法还有许多，例如：遗传算法、烟花算法、蚁群算法、模拟退火算法等等。

一、神经网络算法步骤

1、导入需要处理的数据，随机获取实验数据和目标数据。

2、构建训练网络，函数：newwff。

3、对网络训练，函数：train。

4、仿真操作，函数：sin(net,x)。

5、评价。

6、模拟训练的效果可视化。

在神经网络训练中，我们构建神经网络的实验数据和目标收敛数据都是从原始数据中随机获取的。

二、神经网络学习主要函数说明

newff：前馈网络创建函数
函数结构：net = newff(A,B,{C},’trainFun’,’BLF’,’PF’)。
参数：
A：一个n*2的矩阵，第i行元素为输入信号Xi的最大最小值；
B：一个K维行向量，其元素为网络中各个节点的数量；
C：一个K维字符串行向量，每一个分量为对应层的神经元的激活函数，默认为“tansig”；
trainFun：为学习规则的采用的训练算法。默认为：“trainlm”；
BLF：BP权值/偏差学习函数。默认为：“learngdm”；
PF：性能函数，默认为“mse”；
train函数
函数结构
网络学习函数：[net,tr,YI,E] = train(net,X,Y) 。
参数：
X：网络实际输入；
Y：网络应有输出；
tr：网络跟踪信息；
YI：网络实际输出；
E：误差矩阵。
sim函数
函数结构：Y = sim(net,X) 。
参数
X：输入给网络的KN矩阵，K为网络输入个数，N为样本数据量；
Y：输出矩阵QN,其中Q为网络输出个数。

三、案例

1．案例1

利用三层BP神经网络来完成非线性函数的逼近任务，其中隐层神经元个数为五个。

clear; clc;X=-1:0.1:1;D=[-0.9602 -0.5770 -0.0729 0.3771 0.6405 0.6600 0.4609...0.1336 -0.2013 -0.4344
-0.5000 -0.3930 -0.1647 -.0988...0.3072 0.3960 0.3449
0.1816 -0.312 -0.2189 -0.3201];net=newff([-1,1],[5,1],{'tansig','tansig'});%初始网络net.trainParam.epochs=1000;%最大训练次数net.trainParam.goal=0.005;%训练要求精度net=train(net,X,D);%网络训练figureplot(X,D,'*',X,Y); %绘制实际曲线点和预测曲线% 利用得到的神经网络和数据仿真预测Y=sim(net,X)  %Y为预测结果

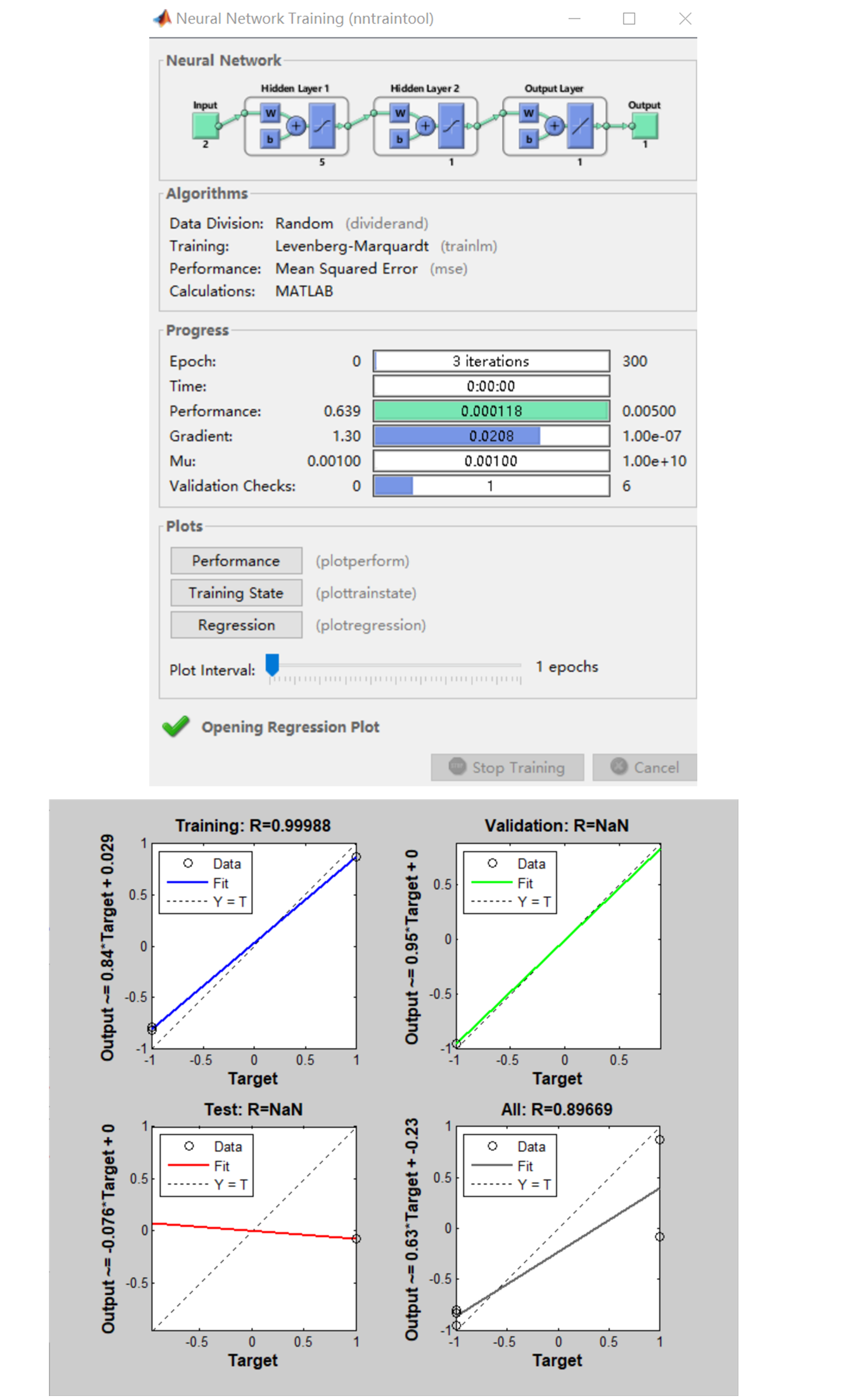
在这里插入图片描述

2．案例2

clear;clc;P=[-1 -1 2 2 4;0
5 0 5 7];T=[-1 -1 1 1
-1];% 样本数据归一化处理[input_n,input_ps]=mapminmax(P);[output_n,output_ps]=mapminmax(T);% 初始化网络结果（利用minmax函数求输入样本范围）net=newff(input_n,output_n,[5,1]);%三个数据为输入样本数据，输出样本数据和隐含层节点数%设置参数net.trainParam.show=50;net.trainParam.lr=0.05;net.trainParam.epochs=300;net.trainParam.goal=0.005;%网络训练[net,tr]=train(net,P,T);%利用得到的神经网络和数据仿真预测Y=sim(net,P)%Y为预测结果

在这里插入图片描述
以上是BP神经网络的相关介绍，BP神经网络适用于大样本数据的预测，至于小样本还有灰色理论、最小二乘支持向量机、广义回归神经网络、灰色神经网络，不同的数据需要根据其自身特点选择不同的预测方法。在很多次实验之后，我比较钟情于BP神经网络和组合预测，组合预测是大趋势，客观上有道理，主观上有更大的操作可能性。
下面给出广义回归神经网络（包含交叉验证过程的GRNN）用于小样本量预测的代码，包括BP神经网络预测结果的对比。
GRNN预测，BP对比