伸展树的代码实现

一、伸展树的数据结构

typedef struct Node
{int key;    struct Node *lch,*rch,*parent;
}* Node ,* Tree;

二、伸展树的基础操作

下面几个函数中，设x 的父节点为 p, p的父节点为g 。

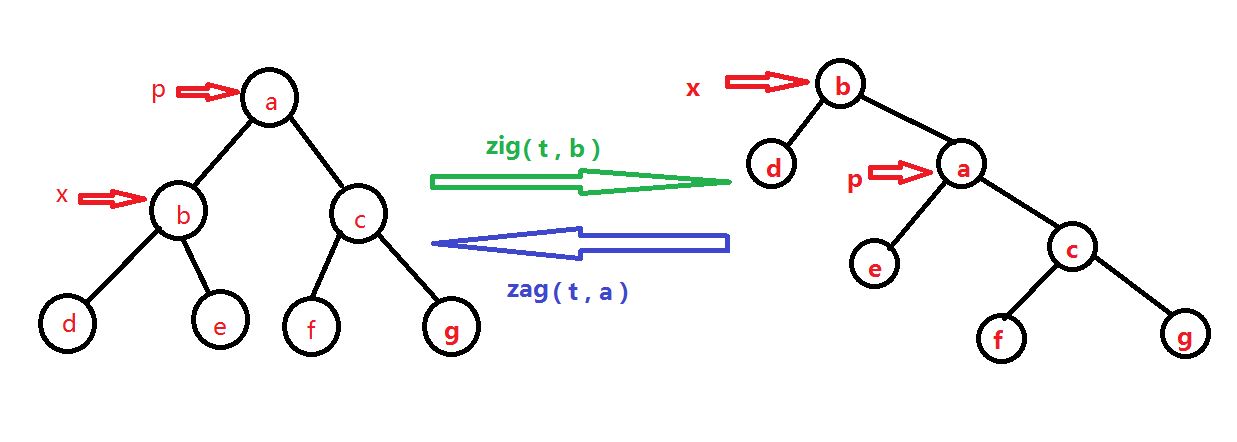
zig( t , x )
右旋。当p是根节点，x是p的左孩子，将x右旋。

代码如下：

//单次右旋以 root 节点 为根节点的树 
Node zig( Tree tree , Node root)
{Node lc = root->lch;Node parent = root->parent;//处理父节点关系 if( parent ){if( root == parent->lch ){parent->lch = lc;}else{parent->rch = lc;}lc->parent = parent;}else{lc->parent = NULL;}//翻转 if( lc != NULL ){root->lch = lc->rch;if( lc->rch ){lc->rch->parent = root;} lc->rch = root;root->parent = lc;if( parent ){return tree;}else{return lc;  }}return tree;
}

zag( t , x )
左旋。当p是根节点，x是p的右孩子，将x左旋

//单次左旋以 root 节点 为根节点的树 
Node zag( Tree tree , Node root)
{Node rc = root->rch;Node parent = root->parent;//处理父节点关系 if( parent ){if( root == parent->lch ){parent->lch = rc;}else{parent->rch = rc;}rc->parent = parent;}else{rc->parent = NULL;}//翻转 if( rc != NULL ){root->rch = rc->lch;if( rc->lch ){rc->lch->parent = root;} rc->lch = root;root->parent = rc;if( parent ){return tree;}else{return rc;  }}return tree;
}

zig_zig( t , x )
右双旋。x是p的左节点，当p是g的左节点，先将p右旋，再将x右旋

//右双旋以 root 节点 为根节点的树 
Node zig_zig( Tree tree , Node root)
{Node lc = root->lch;Node node=zig( tree , root );return zig( node , lc );
}

zag_zag( t , x )
左双旋。x是p的右节点，当p是g的右节点，先将p左旋，再将x左旋

//左双旋以 root 节点 为根节点的树 
Node zag_zag( Tree tree , Node root)
{Node rc = root->rch;Node node=zag( tree , root );return zag( node , rc );
}

zig_zag( t , x )
右旋再左旋。x是p的左节点，当p是g的右节点，先将x右旋，再将x左旋

Node zig_zag( Tree tree , Node root)
{Node node=zig( tree , root->rch );return zag( node , root );
}

zag_zig( t , x )
左旋再右旋。x是p的右节点，当p是g的左节点，先将x左旋，再将x右旋

Node zag_zig( Tree tree , Node root)
{Node node=zag( tree , root->lch ); return zig( node , root );
}

zig_zag_manager( t , x)
旋转管理者。找到x，分析x与父亲节点，父亲节点与祖父节点的关系，选择恰当的旋转方式。

//根据目标节点的结构选择相应的算法，策略模式 
Node zig_zag_manager( Tree tree , Node node )
{ Node parent = node->parent;if( parent == tree  )    //1{if( parent->lch == node ){return zig( tree , parent );}else{return zag( tree , parent );}}else if(  parent->lch == node ){ //2Node grand = parent->parent;    if( grand->lch == parent ){ /*左左*/return zig_zig( tree , grand ); }else{                      /*右左*/ return zig_zag( tree , grand );}}else if( parent->rch == node ){ //3Node grand = parent->parent;    if( grand->lch == parent ){ /*左右*/return zag_zig( tree , grand ); }else{                      /*右右*/return zag_zag( tree , grand );}}return tree;
}

splay( t ,x )
将x调至根部。循环调用zig_zag_manager( t , x) 方法，直到x == t

//将目标节点调整到树的根部，并返回树根 
Node splay(Tree tree , Node node)
{while( node->parent!=NULL ){zig_zag_manager( tree , node );}return node;
}

find( t , x )
找到x。找到x，然后将x旋转到树根。

//寻找key节点 
Node find( Tree tree , int key )
{Node curr = tree;while( curr != NULL ){if( curr->key == key ){splay( tree , curr );return curr;    } else if( curr->key > key ){curr = curr->lch;}else{curr = curr->rch;}}return NULL;
}

spilt( t , x)
以x为界分离t。找到x,将x旋转到树根，然后将x的左子树和剩余部分分离

//以 node 为届，分离 tree 的左子树 ,返回剩余部分 
Node spilt( Tree tree , Node node )
{tree = splay( tree , node ); //将 node 调至根部Node lc = tree->lch;tree->lch = NULL;if( lc ) {lc->parent = NULL;}return tree;
}

注意这里，要获得左子树可以在分离之前获得。

join( t1 , t2 )
合并子树 t1和t2，要求t1所有元素小于t2的任一元素。找到t1的最大元素，并调整到根部，将t2作为根的右子树插入

//合并tree1 和 tree2 ,要求 tree1 所有元素小于 tree2 任一元素 
Node join( Tree tree1, Tree tree2)
{//找打 tree1 中最大的元素 Node temp = tree1;while( temp->rch != NULL ){temp = temp->rch;} //将 temp调至 tree1的根部 splay( tree1 ,temp );//将 tree2 作为 temp的右子树temp->rch = tree2;tree2->parent = temp;return temp; 
}