城市轮廓线求解

问题描述

每一个建筑物用一个三元组表示(L, H, R), 表示左边界, 高度和右边界,轮廓线用X,Y,X,Y…这样的交替式表示,给N个建筑，求轮廓线。

总体思路

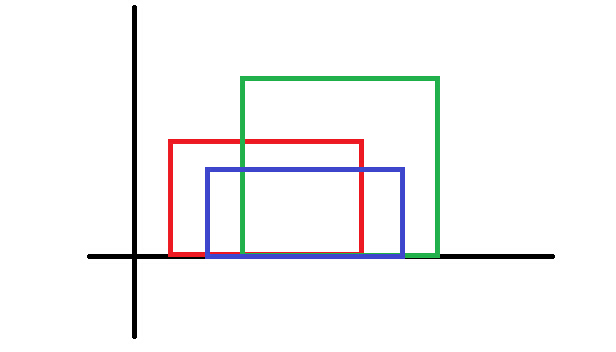
首先，要将建筑物离散成点或线，方便运算。将建筑物表示成（L,H）,(R,H)两个坐标表示，这样原来方块形的建筑物就离散成两条竖线。将所有的竖线按x坐标大小排序。
接下来，将排好序的数组的元素依次插入大顶堆（y坐标为key），如果堆中有与其y坐标相同的元素,则删除该元素（表示该建筑物已结束），否则直接插入堆中。简而言之，关注堆顶元素的变化，只要堆顶元素变化了，就输出堆顶元素的xy值。注意：如果是删除操作导致堆顶元素变化，输出的值应该为当前x值（curr_x），如果删除后，堆为空，那么y应该输出（curr_x,0）；

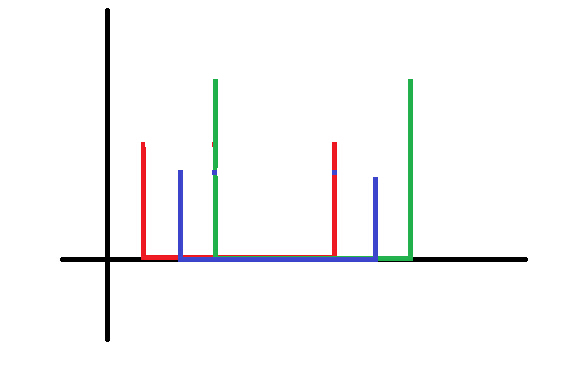
示意图

输入：
这里写图片描述

离散化：
这里写图片描述

过程描述：
这里写图片描述

代码

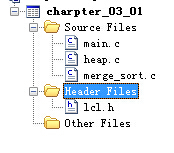
工程结构：
这里写图片描述

可以看到，需要一个大顶堆（优先队列）——heap.c，一个排序算法，这里是归并排序——merge.c，作为辅助。

而关键代码只有如下几行：

//计算出天际线 ，输入已按x排好序的点数组 points , 和点数组的长度
void get_sky_line(struct Point* points,int length)
{/*实现原理：只要关注堆首元素的变化和堆为空时的处理即可。堆首元素变化只有两种情况，插入或删除事件点 */ struct Heap* heap =(struct Heap*)malloc( sizeof( struct Heap ) );struct Point array[ length ];heap->points = array;heap->size = 0;heap->length = length;struct Point p,old_max, new_max;         int i,curr_x,index;for( i=0 ; i<length ; i++ ){if( (index=exist(heap , points[i])) != -1 )  {p = heap->points[ index ]; curr_x = points[i].x;delete_i(heap , index);//print_heap(heap);if( heap->size == 0 ){p.y = 0;p.x = curr_x;add_to_result( p );   //1 }else if( index==0 ){ //首元素发生了变化 p = heap->points[ 0 ];p.x = curr_x;add_to_result( p );   //2} }else{old_max = heap->points[ 0 ];insert( heap , points[i] ); //print_heap(heap);new_max = heap->points[ 0 ];if( !point_equal(old_max , new_max)) //首元素发生了变化 {add_to_result( new_max ); //3}} }} int init(int bd_num)
{int i,j,left,height,right,ps_num=bd_num*2;struct Point points[ps_num];//输入建筑物参数printf("建筑参数为left height right形式，以空格分隔。\n");for(i=0,j=1;i<ps_num;i=i+2,j++){printf("输入建筑%d参数：",j);scanf("%d %d %d",&left,&height,&right);points[i].x=left;points[i].y=height;points[i+1].x=right;points[i+1].y=height;       }merge_sort(points,0,ps_num-1);   //将事件点排序   get_sky_line( points , ps_num );  //得到轮廓线}