最基本的二分查找算法

「搜索区间」是 [left, right]
nums[mid] == target 时可以立即返回

int binary_search(int[] nums, int target) {int left = 0, right = nums.length - 1; while(left <= right) {int mid = left + (right - left) / 2;//防止大数溢出if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1; } else if(nums[mid] == target) {// 直接返回return mid;}}// 直接返回return -1;
}

普通版寻找左侧边界的二分查找

「搜索区间」是 [left, right)
{1,2,2,2,3}
nums[mid] == target 时不要立即返回，要收紧右侧边界以锁定左侧边界

int left_bound(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定左侧边界right = mid - 1;}}// 最后要检查 left 越界的情况if (left >= nums.length || nums[left] != target)return -1;return left;
}

普通版寻找右侧边界的二分查找

「搜索区间」是 [left, right)
{1,2,2,2,3}
nums[mid] == target 时不要立即返回，收紧左侧边界以锁定右侧边界

int right_bound(int[] nums, int target) {int left = 0, right = nums.length - 1;while (left <= right) {int mid = left + (right - left) / 2;if (nums[mid] < target) {left = mid + 1;} else if (nums[mid] > target) {right = mid - 1;} else if (nums[mid] == target) {// 别返回，锁定右侧边界left = mid + 1;}}// 最后要检查 right 越界的情况if (right < 0 || nums[right] != target)return -1;return right;
}

排除法思考二分法

1、确定搜索区间初始化时候的左右边界，有时需要关注一下边界值。在初始化时，有时把搜索区间设置大一点没有关系，但是如果恰好把边界值排除在外，再怎么搜索都得不到结果。

2、无条件写上 while (left < right) ，表示退出循环的条件是 left == right，对于返回左右边界就不用思考了，因此此时它们的值相等；

3、先写下取整的中间数取法，然后从如何把 mid 排除掉的角度思考 if 和 else 语句应该怎样写。

（这里建议写两个注释。）

• 一般而言，我都会把**“什么时候不是目标元素”**作为注释写在代码中，提醒自己要判断正确，这一步判断非常关键，直接影响到后面的代码逻辑。
• 然后接着思考 mid 不是解的情况下，mid 的左右两边可能存在解，把下一轮搜索的区间范围作为注释写进代码里，进而在确定下一轮搜索区间边界的收缩行为时，不容易出错。

if 有把握写对的情况下，else 就是 if 的反面，可以不用思考，直接写出来。

** 说明：这种思考方式，就正正好把待搜索区间从逻辑上分成两个区间，一个区间不可能存在目标元素，进而在另一个区间里继续搜索，更符合“二分”的语义。**

4、根据 if else 里面写的情况，看看是否需要修改中间数下取整的行为。


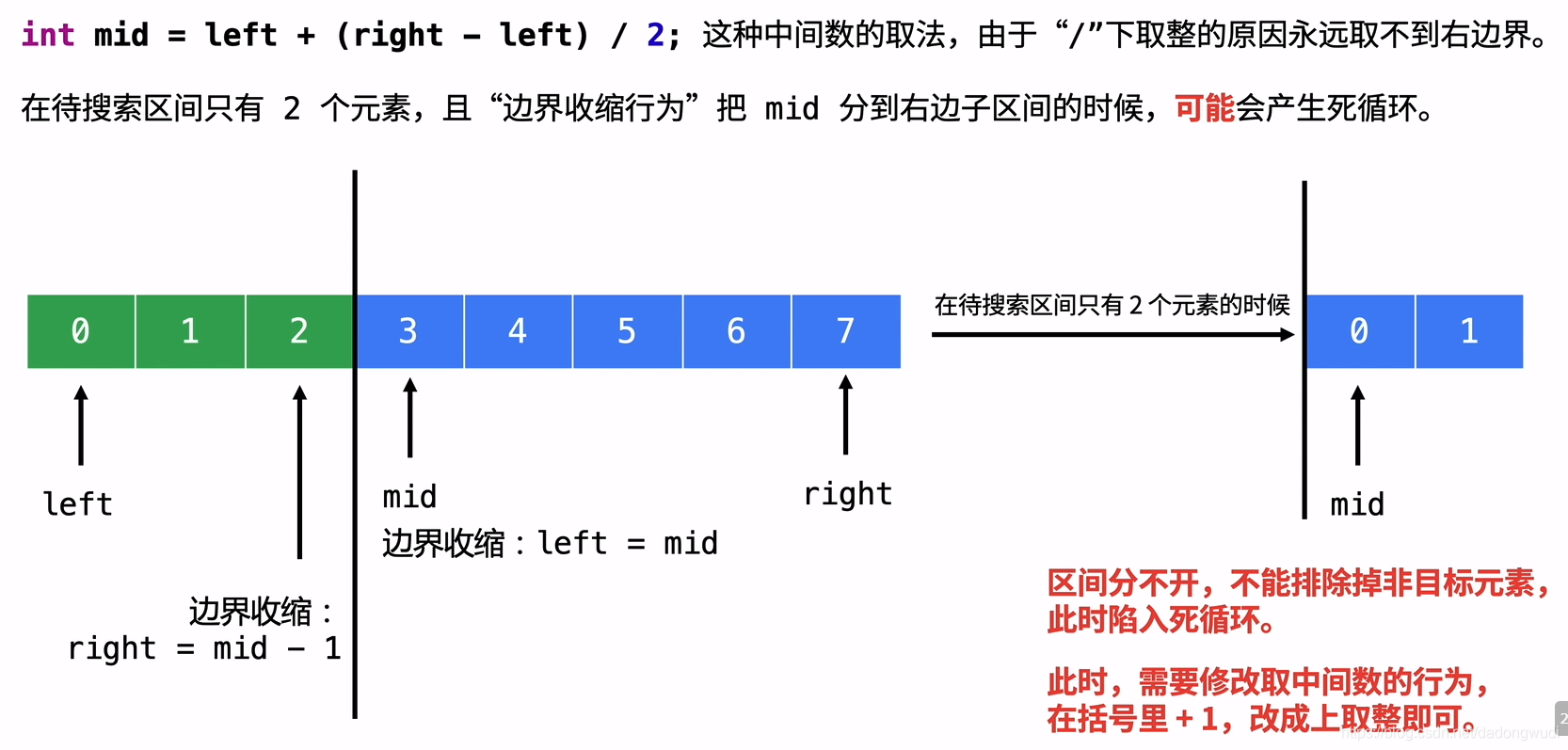
上面已经说了，只有看到 left = mid 的时候，才需要调整成为上取整，记住这一点即可，我因为刚开始不理解这种写法，遇到很多次死循环，现在已经牢记在心了。

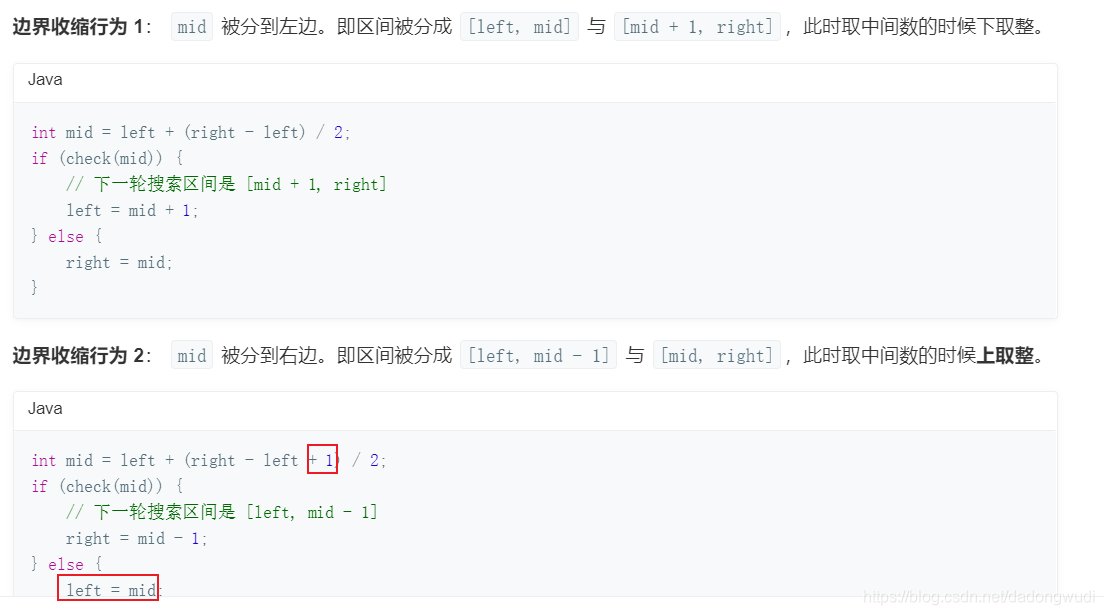
5、退出循环的时候，一定有 left == right 成立。有些时候可以直接返回 left （或者 right，由于它们相等，后面都省略括弧）或者与 left 相关的数值，有些时候还须要再做一次判断，判断 left 与 right 是否是我们需要查找的元素，这一步叫“后处理”。

// 有可能区间内不存在目标元素，因此还需做一次判断if (nums[left] == target) {return left;}return  -1;

public int searchInsert(int[] nums, int target) {int len = nums.length;if (len == 0) {return 0;}int left = 0;// 因为有可能数组的最后一个元素的位置的下一个是我们要找的，故右边界是 lenint right = len;while (left < right) {int mid = (left + right) >>> 1;// 小于 target 的元素一定不是解if (nums[mid] < target) {// 下一轮搜索的区间是 [mid + 1, right]left = mid + 1;} else {right = mid;}}return left;}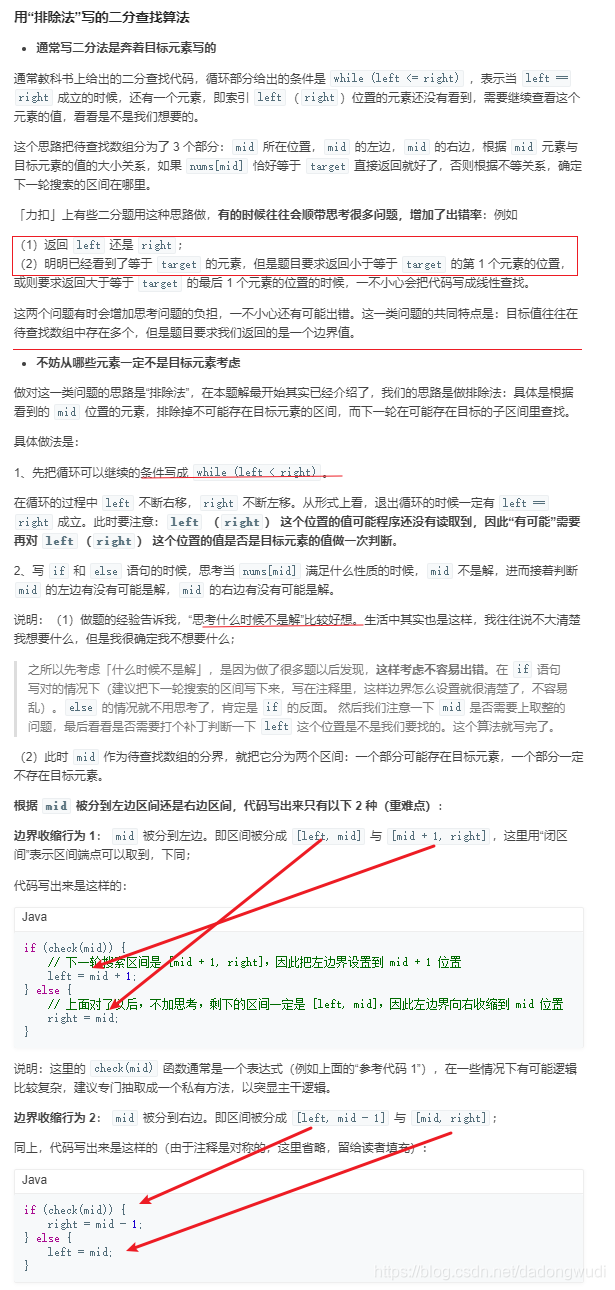

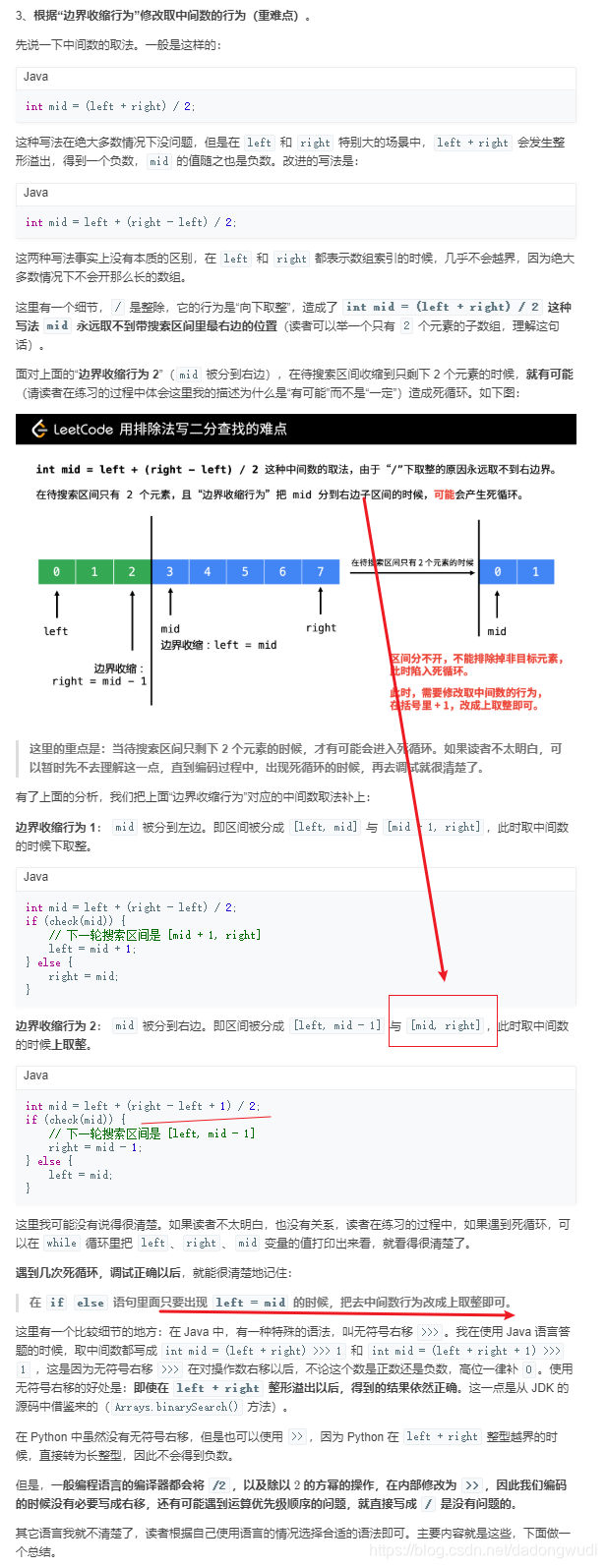
二分查找模板 一般步骤

与其他二分查找的比较

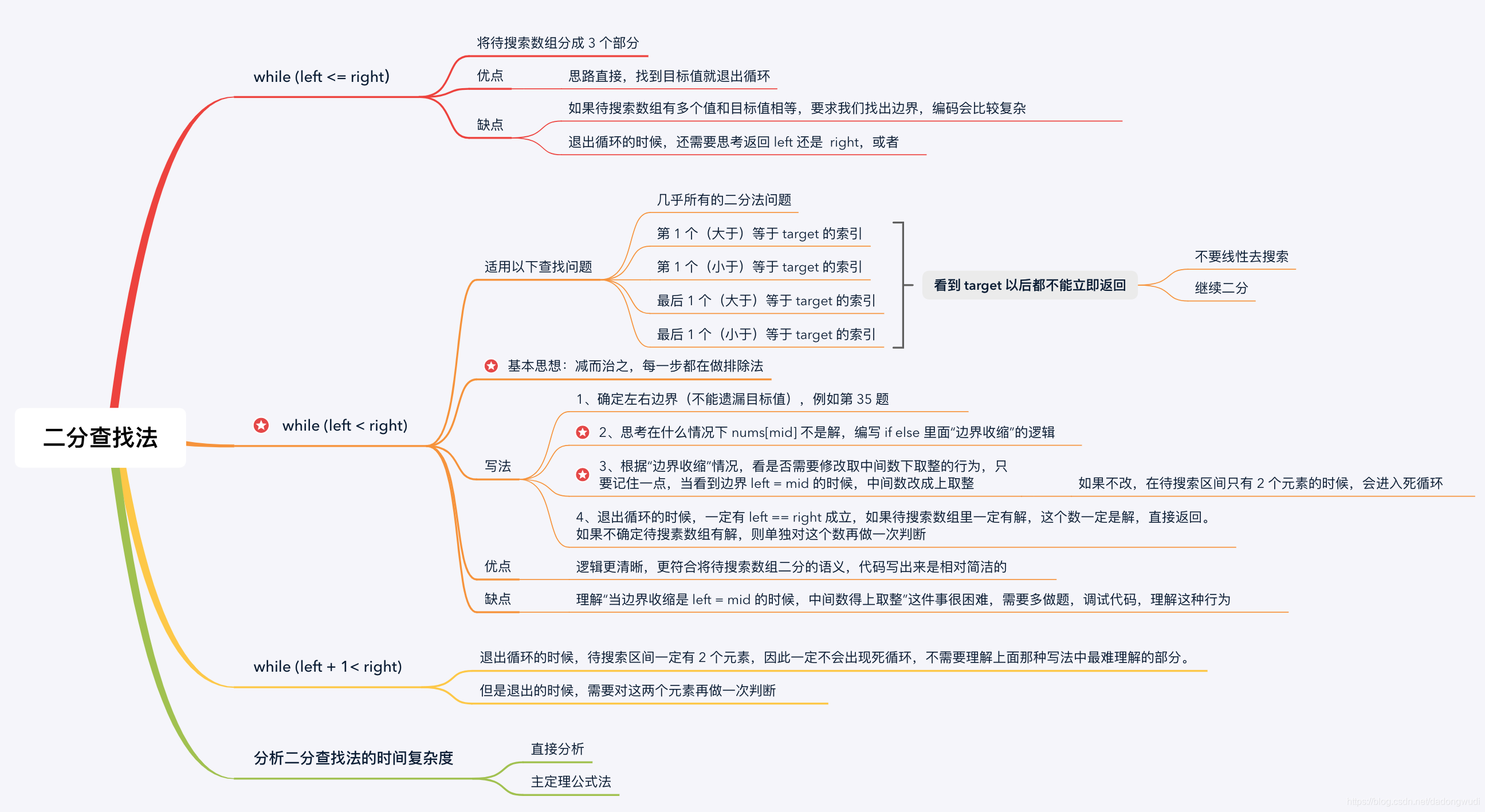
[总结]

1.普通版

-左右移动下标时，mid下标对应的值已经作为比较，故坐标更新时需要加一减一

2.防止大数溢出

• mid = left + (right - left) / 2

3.完整掌握二分查找需要注意细节，善用排除法

参考链接：https://github.com/Arthashuo/fucking-algorithm/blob/master/%E7%AE%97%E6%B3%95%E6%80%9D%E7%BB%B4%E7%B3%BB%E5%88%97/%E4%BA%8C%E5%88%86%E6%9F%A5%E6%89%BE%E8%AF%A6%E8%A7%A3.md

参考链接：https://leetcode-cn.com/problems/search-insert-position/solution/te-bie-hao-yong-de-er-fen-cha-fa-fa-mo-ban-python-/