凸包是啥？？

凸包就是：

给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。

外层的红线　就是凸包

一般题目会让你求利用最外层凸包的一些性质如下面这道题

来看一道模板题：ＨＤＵ　－　１３４８

本题题目就是要求尽可能少的围墙周长 围墙内的城堡是多边形的 而围墙还要和城堡相隔l距离

可证 实质周长其实就是 城堡的凸包周长 + 以l为半径的周长之和 

由于多边形城堡 尽可能少的包围他其实就是凸包周长 而在凸包的拐角处 要相隔l距离 所以变成了一个圆弧

把圆弧加起来就是圆的周长 

n边形的内角和公式 ：（n-2）*180

n变形外角永远是360度

所以 可以列式 n×360 - (n-2)×180 -９０×n×２ = 360° （n个角 减去内角 在减去多余的90° 画个图就能得到）

所以多出来的那些空间可知就是一个360°的整圆

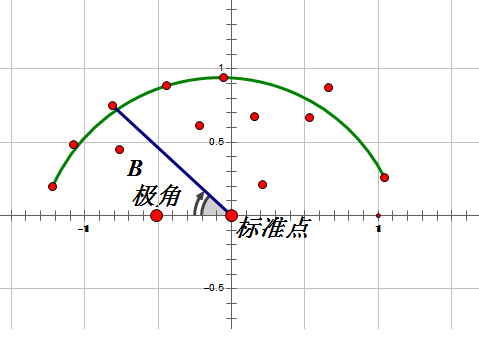
关于这个方法就是先取左下点为基准点 

 然后 对其他点 按照从基准点的x轴逆时针方向射出的极角 扫过的顺序排序 

然后再对其中的每前后三个点进行叉乘操作

 

 如果我们以逆时针方向遍历所有点

ｎ，ｍ，ｌ三个点　

ｎ为起点　向ｍ和ｌ点做两个向量分别是向量ａ，向量ｂ

向量a*b<0 说明 a在 b的逆时针方向 　即是说　ｍ点在ｌ点里面，左边　若选凸包 我们舍弃a的终点ｍ 而选取b的终点 

若叉乘结果>0说明ａ在ｂ的顺时针方向　也就是　ｍ在ｌ的外边　右边

最终将保存下来的点　按顺序遍历求两点之间的线段长度就可以了

code

#include<bits/stdc++.h>using namespace std;
typedef long long ll;
const int maxn = 1010;
const double pi = acos(-1.0);// 得到PI
struct node
{double x,y;
}p[1010],P[1010];//P内存储凸包内的店
int t,tot,N;
double L;
double X(node a,node b,node c)
{return (b.x-a.x)*(c.y-a.y)-(c.x-a.x)*(b.y-a.y);
}// 计算叉积
double len(node a,node b)
{return sqrt((b.x-a.x)*(b.x-a.x)+(b.y-a.y)*(b.y-a.y));
}//两点之间距离公式
bool cmp(node b,node c)
{double pp = X(p[1],b,c);if(pp<0)return 0;else if(pp>0)return 1;else if(pp==0&&len(p[1],b)<len(p[1],c))return 1;else return 0;
}//扫描排序
int main()
{scanf("%d",&t);for(int cas = 1;cas<=t;cas++){if(cas!=1)puts("");scanf("%d%lf",&N,&L);for(int i=1;i<=N;i++)scanf("%lf%lf",&p[i].x,&p[i].y);double ans = pi*2.0*L;for(int i=2;i<=N;i++){if(p[1].y>p[i].y)swap(p[1],p[i]);else if(p[1].y==p[i].y&&p[1].x>p[i].x)swap(p[1],p[i]);}//找基准点sort(p+2,p+1+N,cmp);P[1]=p[1];P[2]=p[2];tot=2;for(int i=3;i<=N;i++){while(tot>1&&X(P[tot-1],P[tot],p[i])<=0)tot--;tot++;P[tot] = p[i];}//筛选点for(int i=1;i<tot;i++){ans+=len(P[i],P[i+1]);}//围圈求和ans+=len(P[1],P[tot]);printf("%.0lf\n",ans);}return 0;
}