【问题描述】[简单]

判断一个整数是否是回文数。回文数是指正序（从左向右）和倒序（从右向左）读都是一样的整数。示例 1:输入: 121
输出: true
示例 2:输入: -121
输出: false
解释: 从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。

【解答思路】

1. 整形转字符串/字符数组（额外空间）

1.x小于0 直接返回false
2.整形转为字符串后再转为字符数组
3.双指针一头一尾遍历字符数组，判段是否是回文数

时间复杂度：O(N) 空间复杂度：O(N)

class Solution {public boolean isPalindrome(int x) {String reversedStr = (new StringBuilder(x + "")).reverse().toString();return (x + "").equals(reversedStr);}
}

public boolean isPalindrome(int x) {if(x<0){return false;}char[] ch = String.valueOf(x).toCharArray();int len =  ch.length;int i = 0 ;int j = len-1;while(i<j){if(ch[i]!=ch[j]){return false;}i++;j--;}return true;}

2. 数字反转（可能溢出）

• 如果是负数则一定不是回文数，直接返回 false
• 如果是正数，则将其倒序数值计算出来，然后比较和原数值是否相等
• 如果是回文数则相等返回 true，如果不是则不相等 false

比如 123 的倒序 321，不相等；121 的倒序 121，相等

时间复杂度：O(N) 空间复杂度：O(1)

public boolean isPalindrome(int x) {if(x < 0)return false;int cur = 0;int num = x;while(num != 0) {cur = cur * 10 + num % 10;num /= 10;}return cur == x;}

2. 数字反转一半

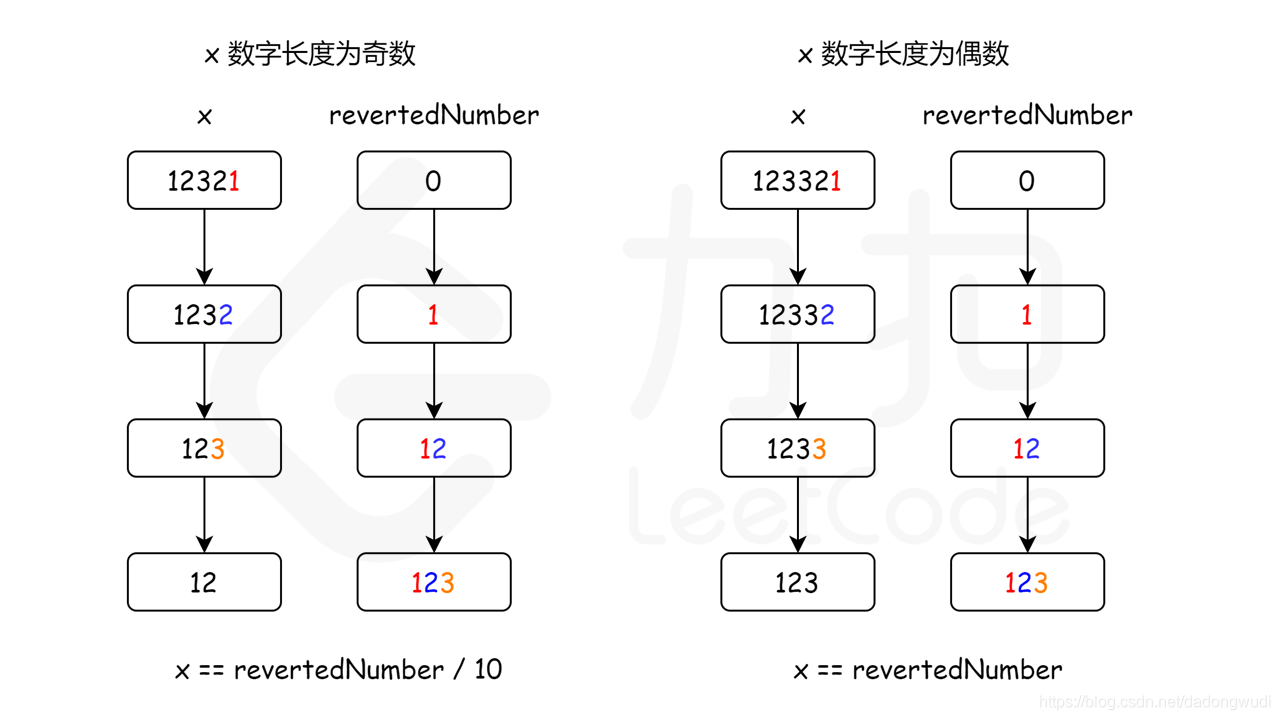
时间复杂度：O(N) 空间复杂度：O(1)

class Solution {public boolean isPalindrome(int x) {// 特殊情况：// 如上所述，当 x < 0 时，x 不是回文数。// 同样地，如果数字的最后一位是 0，为了使该数字为回文，// 则其第一位数字也应该是 0// 只有 0 满足这一属性if (x < 0 || (x % 10 == 0 && x != 0)) {return false;}int revertedNumber = 0;while (x > revertedNumber) {revertedNumber = revertedNumber * 10 + x % 10;x /= 10;}// 当数字长度为奇数时，我们可以通过 revertedNumber/10 去除处于中位的数字。// 例如，当输入为 12321 时，在 while 循环的末尾我们可以得到 x = 12，revertedNumber = 123，// 由于处于中位的数字不影响回文（它总是与自己相等），所以我们可以简单地将其去除。return x == revertedNumber || x == revertedNumber / 10;}
}

【总结】

1.越是简单题 往往含有的思想越巧妙

2.细节：

2.1 逆算数

while(num != 0) {cur = cur * 10 + num % 10;num /= 10;}

2.2 整形转字符数组

int x;
char[] ch = String.valueOf(x).toCharArray();

参考链接：https://leetcode-cn.com/problems/palindrome-number/solution/hua-jie-suan-fa-9-hui-wen-shu-by-guanpengchn/

参考链接：https://leetcode-cn.com/problems/palindrome-number/solution/hui-wen-shu-by-leetcode-solution/

参考链接：https://leetcode-cn.com/problems/palindrome-number/solution/dong-hua-hui-wen-shu-de-san-chong-jie-fa-fa-jie-ch/