[剑指offer]面试题第[57]题[Leetcode][第167题][第1题]
有序无序之分 题目输出不同之分 以下解法按照[剑指offer]面试题第[57]题进行题解

【问题描述】[简单]

输入一个递增排序的数组和一个数字s，在数组中查找两个数，使得它们的和正好是s。如果有多对数字的和等于s，则输出任意一对即可。示例 1：输入：nums = [2,7,11,15], target = 9
输出：[2,7] 或者 [7,2]
示例 2：输入：nums = [10,26,30,31,47,60], target = 40
输出：[10,30] 或者 [30,10]

【解答思路】

1. HashSet（有序无序均可）

时间复杂度：O(N) 空间复杂度：O(N)

 public int[] twoSum(int[] nums, int target) {HashSet<Integer> set = new HashSet<>();for(int num:nums){set.add(num);}for(int num:nums){if(set.contains(target-num)){int[] res = new int[2];res[0] = num;res[1] =target -num;return res;}}return  new int[0];}

优化

public int[] twoSum(int[] nums, int target) {Set<Integer> set = new HashSet<>();for (int num : nums) {if (!set.contains(target - num))set.add(num);else return new int[]{num, target - num};}return new int[]{};}

2. 二分+双指针（有序）

时间复杂度：O(N) 空间复杂度：O(1)

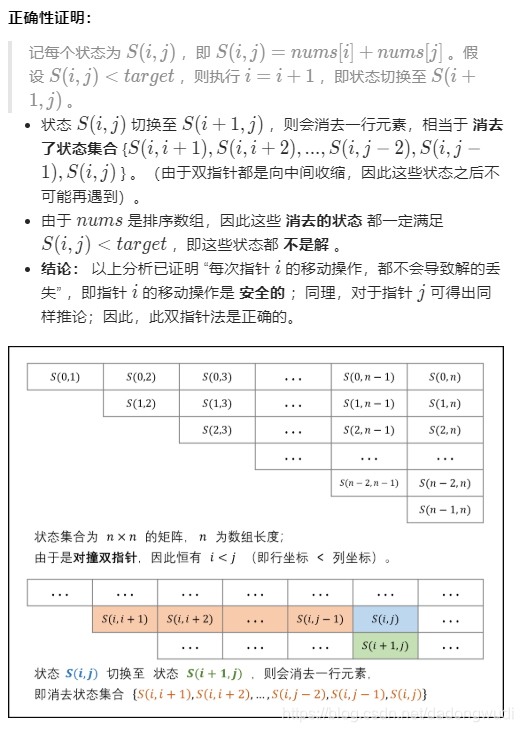
 public int[] twoSum(int[] nums, int target) {int i = 0, j = nums.length - 1;while(i < j) {int s = nums[i] + nums[j];if(s < target) i++;else if(s > target) j--;else return new int[] { nums[i], nums[j] };}return new int[0];}

3. 二分查找（有序）

在数组中找到两个数，使得它们的和等于目标值，可以首先固定第一个数，然后寻找第二个数，第二个数等于目标值减去第一个数的差。利用数组的有序性质，可以通过二分查找的方法寻找第二个数。为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。

时间复杂度：O(NlogN) 空间复杂度：O(1)

public int[] twoSum(int[] numbers, int target) {for (int i = 0; i < numbers.length; ++i) {//为了避免重复寻找，在寻找第二个数时，只在第一个数的右侧寻找。int low = i + 1, high = numbers.length - 1;while (low <= high) {int mid = (high - low) / 2 + low;if (numbers[mid] == target - numbers[i]) {return new int[]{numbers[mid], target - numbers[i]};} else if (numbers[mid] > target - numbers[i]) {high = mid - 1;} else {low = mid + 1;}}}return new int[]{-1, -1};}

4. 暴力（不建议）

时间复杂度：O(N^2) 空间复杂度：O(1)

public int[] twoSum(int[] nums, int target) {for (int i = 0; i < nums.length; i++) {for (int j = i + 1; j < nums.length; j++) {if (nums[j] == target - nums[i]) {return new int[] { nums[j], nums[i] };}}}return new int[] { -1, -1 };}

【总结】

1. 有序数组 二分法

2.HashSet 边添加边寻找 成对的第一个数添加入集合 成对的另一个数会检查入集合时返回正确的一对数

3.细节

返回数组
return new int[] { nums[i], nums[j] };
返回空数组
return new int[0];
return new int[]{};

3.面试 问清楚需求条件 暴力<HashSet<二分法<双指针