【问题描述】[中等]

【解答思路】

1. 动态规划流程

第 1 步：设计状态

第 2 步：状态转移方程

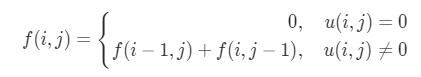
第 3 步：考虑初始化
第一行第一列 没有遇到“障碍” 就为1 如果u（i，j）==0 直接返回 0
第 4 步：考虑输出
右下角： f(i, j)
时间复杂度：O(N^2) 空间复杂度：O(N^2)

public int uniquePathsWithObstacles(int[][] obstacleGrid) {int row = obstacleGrid.length;int col = obstacleGrid[0].length;int[][] grid = new int[row][col];if(obstacleGrid[0][0]==1){return 0;}for(int i = 0;i<row;i++){if( obstacleGrid[i][0]==1){break;}grid[i][0] = 1; }for(int j = 0 ;j<col;j++){if( obstacleGrid[0][j] ==1){break;}grid[0][j] =1;}for(int i = 1;i<row;i++){for(int j = 1 ;j<col;j++){if(obstacleGrid[i][j] ==0){grid[i][j] =grid[i-1][j]+grid[i][j-1];}}}return grid[row-1][col-1];}

2. 动态规划状态压缩

时间复杂度：O(NM) 空间复杂度：O(M)

class Solution {public int uniquePathsWithObstacles(int[][] obstacleGrid) {int n = obstacleGrid.length, m = obstacleGrid[0].length;int[] f = new int[m];f[0] = obstacleGrid[0][0] == 0 ? 1 : 0;for (int i = 0; i < n; ++i) {for (int j = 0; j < m; ++j) {if (obstacleGrid[i][j] == 1) {f[j] = 0;continue;}if (j - 1 >= 0 && obstacleGrid[i][j - 1] == 0) {f[j] += f[j - 1];}}}return f[m - 1];}
}

【总结】

1.动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2.动态规划特点

3. 滚动数组思想压缩

用一维数组暂且保存上一次遍历的结果 ，时刻更新 ，降低二维数组到一维数组

参考链接：https://leetcode-cn.com/problems/unique-paths-ii/solution/bu-tong-lu-jing-ii-by-leetcode-solution-2/