【问题描述】[中等]

【解答思路】

1. 动态规划

第 1 步：设计状态
f(i,j) 表示 s ₁的前 i个元素和 s₂ 的前 j个元素是否能交错组成 s₃的前 i + j 个元素

第 2 步：状态转移方程

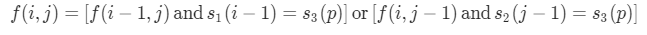
p = i + j - 1 p为s3的长度

第 3 步：考虑初始化
boolean[][] f = new boolean[n + 1][m + 1];
f(0,0)=True
第 4 步：考虑输出
f[n][m];

第 5 步：考虑是否可以状态压缩
时
时间复杂度：O(NM) 空间复杂度：O(NM)

class Solution {public boolean isInterleave(String s1, String s2, String s3) {int n = s1.length(), m = s2.length(), t = s3.length();
//长度之和都不等，肯定无法由s1和s2交替组成s3if (n + m != t) {return false;}boolean[][] f = new boolean[n + 1][m + 1];
//边界条件：认为s1的前0个字符和s2的前0个字符，可以交替组成s3的前0个字符f[0][0] = true;for (int i = 0; i <= n; ++i) {for (int j = 0; j <= m; ++j) {int p = i + j - 1;if (i > 0) {//官方代码前面这个'f[i][j] ||'是没必要的f[i][j] = f[i][j] || (f[i - 1][j] && s1.charAt(i - 1) == s3.charAt(p));}if (j > 0) {//如果前一步i>0时已算出f[i][j]为true，则下面的||会短路，f[i][j]直接就是true了f[i][j] = f[i][j] || (f[i][j - 1] && s2.charAt(j - 1) == s3.charAt(p));}}}
//返回结果：s1的前n个字符和s2的前m个字符，可否交替组成s3的前n+m个字符return f[n][m];}
}

时间复杂度：O(NM) 空间复杂度：O(M)

class Solution {public boolean isInterleave(String s1, String s2, String s3) {int n = s1.length(), m = s2.length(), t = s3.length();if (n + m != t) {return false;}boolean[] f = new boolean[m + 1];f[0] = true;for (int i = 0; i <= n; ++i) {for (int j = 0; j <= m; ++j) {int p = i + j - 1;if (i > 0) {f[j] = f[j] && s1.charAt(i - 1) == s3.charAt(p);}if (j > 0) {f[j] = f[j] || (f[j - 1] && s2.charAt(j - 1) == s3.charAt(p));}}}return f[m];}
}

2. BFS

时间复杂度：O(NM) 空间复杂度：O(NM)

class Solution {public boolean isInterleave(String s1, String s2, String s3) {int n1 = s1.length();int n2 = s2.length();int n3 = s3.length();if (n1 + n2 != n3) return false;//判断是否已经遍历过boolean[][] visited = new boolean[n1 + 1][n2 + 1];Queue<int[]> queue = new LinkedList<>();queue.offer(new int[]{0, 0});while (!queue.isEmpty()) {int[] tmp = queue.poll();/到达右下角就返回 trueif (tmp[0] == n1 && tmp[1] == n2) return true;/ 尝试是否能向右走if (tmp[0] < n1 && s1.charAt(tmp[0]) == s3.charAt(tmp[0] + tmp[1]) && !visited[tmp[0] + 1][tmp[1]]) {visited[tmp[0] + 1][tmp[1]] = true;queue.offer(new int[]{tmp[0] + 1, tmp[1]});}/ 尝试是否能向下走if (tmp[1] < n2 && s2.charAt(tmp[1]) == s3.charAt(tmp[0] + tmp[1]) && !visited[tmp[0]][tmp[1] + 1]) {visited[tmp[0]][tmp[1] + 1] = true;queue.offer(new int[]{tmp[0], tmp[1] + 1});}}return false;}
}

【总结】

1. 动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2. BFS DFS 遍历好助手

转载链接：https://leetcode-cn.com/problems/interleaving-string/solution/jiao-cuo-zi-fu-chuan-by-leetcode-solution/
参考链接：https://leetcode-cn.com/problems/interleaving-string/solution/dong-tai-gui-hua-he-bfs-by-powcai/

参考链接：https://leetcode-cn.com/problems/interleaving-string/solution/xiang-xi-tong-su-de-si-lu-fen-xi-duo-jie-fa-by-2-9/