【问题描述】[中等]

【解答思路】

1动态规划

动态规划流程
第 1 步：设计状态
f(i, j)f(i,j) 为从棋盘左上角走至单元格 (i ,j)(i,j) 的礼物最大累计价值
第 2 步：状态转移方程
f(i,j)=max[f(i,j−1),f(i−1,j)]+grid(i,j)
第 3 步：考虑初始化

第 4 步：考虑输出

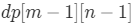
第 5 步：考虑是否可以状态压缩

时间复杂度：O(N^2) 空间复杂度：O(1)

class Solution {public int maxValue(int[][] grid) {//m 列数 n 行数int m = grid.length, n = grid[0].length;for(int j = 1; j < n; j++) // 初始化第一行grid[0][j] += grid[0][j - 1];for(int i = 1; i < m; i++) // 初始化第一列grid[i][0] += grid[i - 1][0];for(int i = 1; i < m; i++)for(int j = 1; j < n; j++) grid[i][j] += Math.max(grid[i][j - 1], grid[i - 1][j]);return grid[m - 1][n - 1];}
}

【总结】

1. 动态规划流程

第 1 步：设计状态
第 2 步：状态转移方程
第 3 步：考虑初始化
第 4 步：考虑输出
第 5 步：考虑是否可以状态压缩

2. 压缩空间可以在原数组上操作 行列

3.想清楚应该加什么，切忌想当然

3.类似题目[Leetcode][第64题][JAVA][64. 最小路径和]

转载链接：https://leetcode-cn.com/problems/li-wu-de-zui-da-jie-zhi-lcof/solution/mian-shi-ti-47-li-wu-de-zui-da-jie-zhi-dong-tai-gu/