[Leetcode]第[43]题[JAVA][字符串相乘][字符串相加]

【问题描述】[中等]

【解答思路】

1. 普通竖式

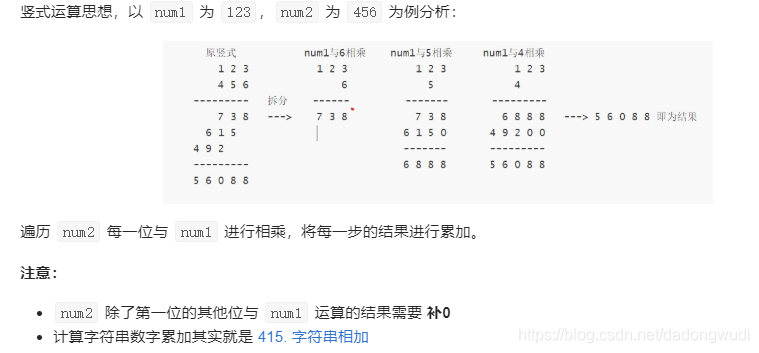
在这里插入图片描述

**复杂度：O(N^2) **
在这里插入图片描述

class Solution {/*** 计算形式*    num1*  x num2*  ------*  result*/public String multiply(String num1, String num2) {if (num1.equals("0") || num2.equals("0")) {return "0";}// 保存计算结果String res = "0";// num2 逐位与 num1 相乘for (int i = num2.length() - 1; i >= 0; i--) {int carry = 0;// 保存 num2 第i位数字与 num1 相乘的结果StringBuilder temp = new StringBuilder();// num2补 0   eg： 6在十位上 在最后结果后面补0（这里倒叙插入）for (int j = 0; j < num2.length() - 1 - i; j++) {temp.append(0);}int n2 = num2.charAt(i) - '0';// num2 的第 i 位数字 n2 与 num1 相乘for (int j = num1.length() - 1; j >= 0 || carry != 0; j--) {int n1 = j < 0 ? 0 : num1.charAt(j) - '0';int product = (n1 * n2 + carry) % 10;temp.append(product);carry = (n1 * n2 + carry) / 10;}// 将当前结果与新计算的结果求和作为新的结果 temp逆转res = addStrings(res, temp.reverse().toString());}return res;}/*** 对两个字符串数字进行相加，返回字符串形式的和*/public String addStrings(String num1, String num2) {StringBuilder builder = new StringBuilder();int carry = 0;for (int i = num1.length() - 1, j = num2.length() - 1;i >= 0 || j >= 0 || carry != 0;i--, j--) {int x = i < 0 ? 0 : num1.charAt(i) - '0';int y = j < 0 ? 0 : num2.charAt(j) - '0';int sum = (x + y + carry) % 10;builder.append(sum);carry = (x + y + carry) / 10;}return builder.reverse().toString();}
}

2. 优化竖式

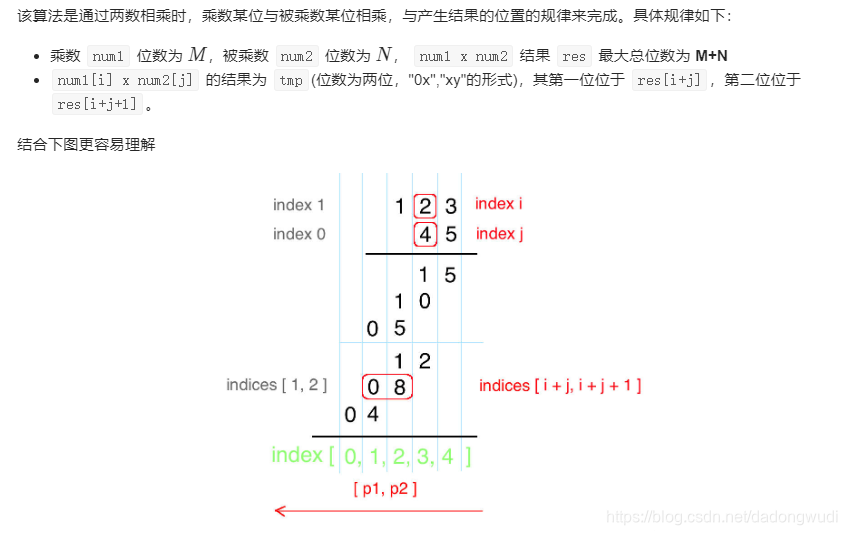
在这里插入图片描述

复杂度
在这里插入图片描述

class Solution {public String multiply(String num1, String num2) {if (num1.equals("0") || num2.equals("0")) {return "0";}int[] res = new int[num1.length() + num2.length()];for (int i = num1.length() - 1; i >= 0; i--) {int n1 = num1.charAt(i) - '0';for (int j = num2.length() - 1; j >= 0; j--) {int n2 = num2.charAt(j) - '0';int sum = (res[i + j + 1] + n1 * n2);res[i + j + 1] = sum % 10;res[i + j] += sum / 10;}}StringBuilder result = new StringBuilder();for (int i = 0; i < res.length; i++) {if (i == 0 && res[i] == 0) continue;result.append(res[i]);}return result.toString();}
}