文章出处：极客时间《数据结构和算法之美》-作者：王争。该系列文章是本人的学习笔记。

1 堆定义

1.1 定义和结构

堆是一个完全二叉树（完全二叉树：除了叶子节点外每一层节点都是满的，最后一层的子节点都靠左排列）；堆中每个节点的值都大于等于（或小于等于）其子树中的每个节点的值。
　　因为堆是一个完全二叉树，所以可以用数组来表示堆。如果根节点存在在下标为1的位置。下标i存储节点，下标2i存储节点的左子节点，2i+1存储节点的右子节点。

1.2 操作和存储结构

1.2.1 插入元素

　　向一个堆中插入一个元素，直接放在最后一个位置可能会破坏堆的结构，于是就需要进行调整。这个过程称为堆化。堆化分为两种：从下向上、从上往下。现在先看从下向上。堆化就是沿着路径不断向上比较，如果不满足大小关系，就交换。直到满足堆条件。
　　

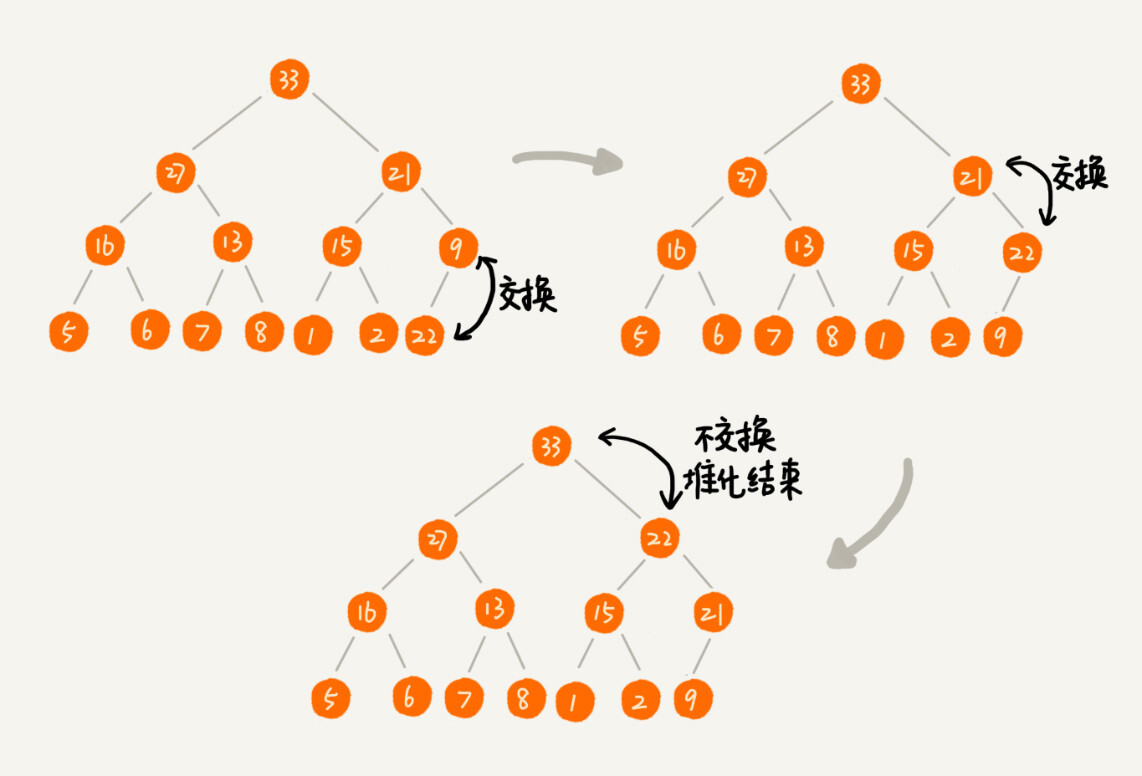
1.2.2 删除堆顶元素

当删除堆顶的元素之后，需要做一些操作才能称为新的堆。假设删除的是一个大顶堆，堆顶放的是最大元素。

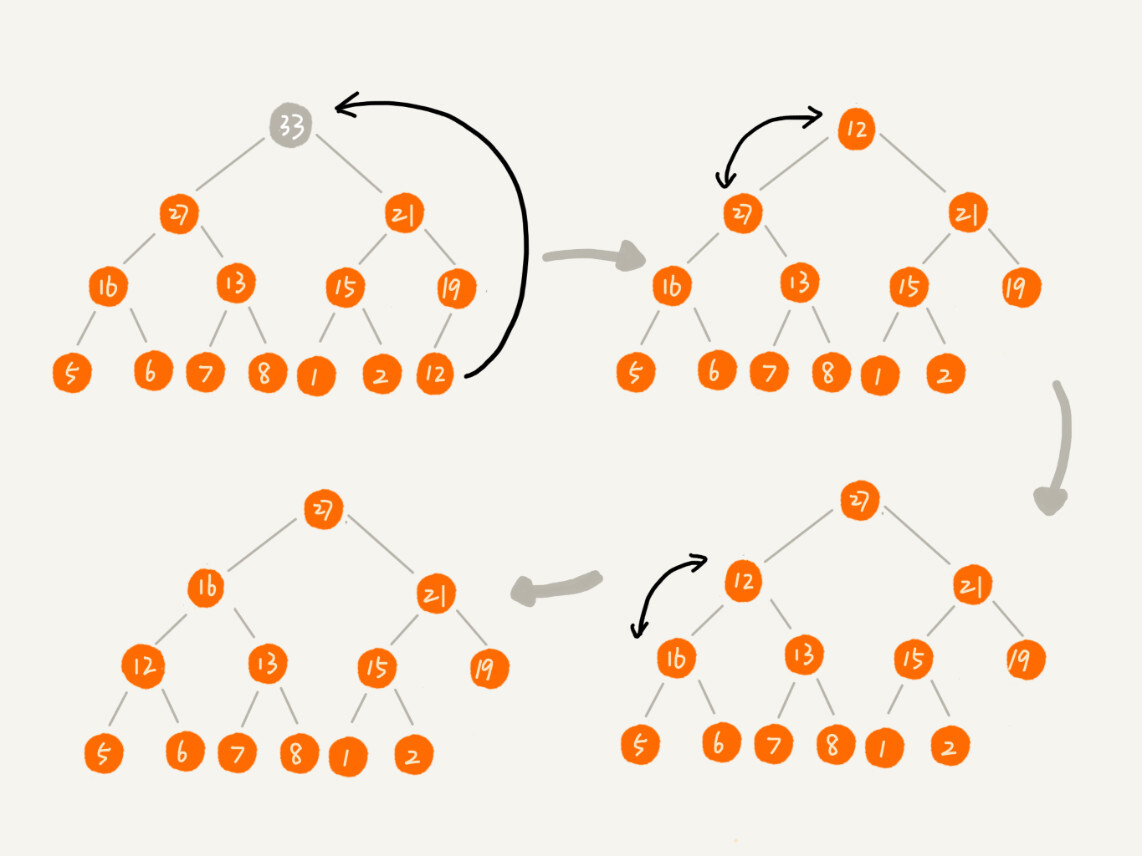
　　删除堆顶元素33，将最后一个节点的值12赋值给根节点。然后对根节点做堆化，从上往下的。如果不满足大小关系，将根节点沿着路径选择较大值的子节点和根节点交换。继续交换直到满足堆定义。

1.3 相关代码

代码

2 堆排序

堆排序时间复杂度是O(nlogn)，是原地排序，但不是稳定排序。堆排序过程分为建堆和排序两个阶段。

2.1建堆

输入一个数组，原地将这个数组建堆，不使用额外的空间。
我们可以把这个过程看作是堆的插入过程。先假设堆起初只包含下标为1的元素。调用插入方法将下标从2到n的数据依次插入。这样建堆就完成了。
第二种处理方法是从后往前处理数据。对每一个数据做从上往下的堆化。也就是说以当前节点为根节点，比较其与子树上每个节点的值，保证符合堆定义。叶子节点堆化只能和自己比较，故，省略，从$\frac{2}{n}$开始处理数据。
如果我们需要从小到大排序数组。在建堆的时候我们可以建一个大顶堆。

2.2 排序

建堆结束，我们已经有了一个大顶堆。堆顶元素是最大的。如果我们把堆顶元素和最后一个元素交换位置，模拟堆顶元素删除操作，将这n-1个元素堆化。继续将堆顶元素和倒数第二个元素交换位置，继续堆化这n-2个元素。直至堆的大小为1，则得到一个从小到大排序的数组。

2.3 时间复杂度

1 用递归树法求建堆的时间复杂度：O(n)。
2 排序时间复杂度：O(nlogn)。
所以最终时间复杂度O(nlogn)。

2.4 为什么使用快排而不是堆排序

1 因为堆排序的比较次数、移动次数比较高。
2 堆排序不是稳定排序。在前后交换过程中会改变数据的前后顺序。
3 数据访问方式是跳跃式的，不利于使用CPU缓存机制。

代码