1 为什么需要RNN

1.1RNN的应用场景

1 模仿论文（生成序列）。输入是一堆的论文文章，输出是符合论文格式的文本。
2 模仿linux 内核代码写程序（生成序列）
3 模仿小四写文章(生成文本序列)

4 机器翻译
5 image to text 看图说话

1.2 DNN和CNN不能解决的问题

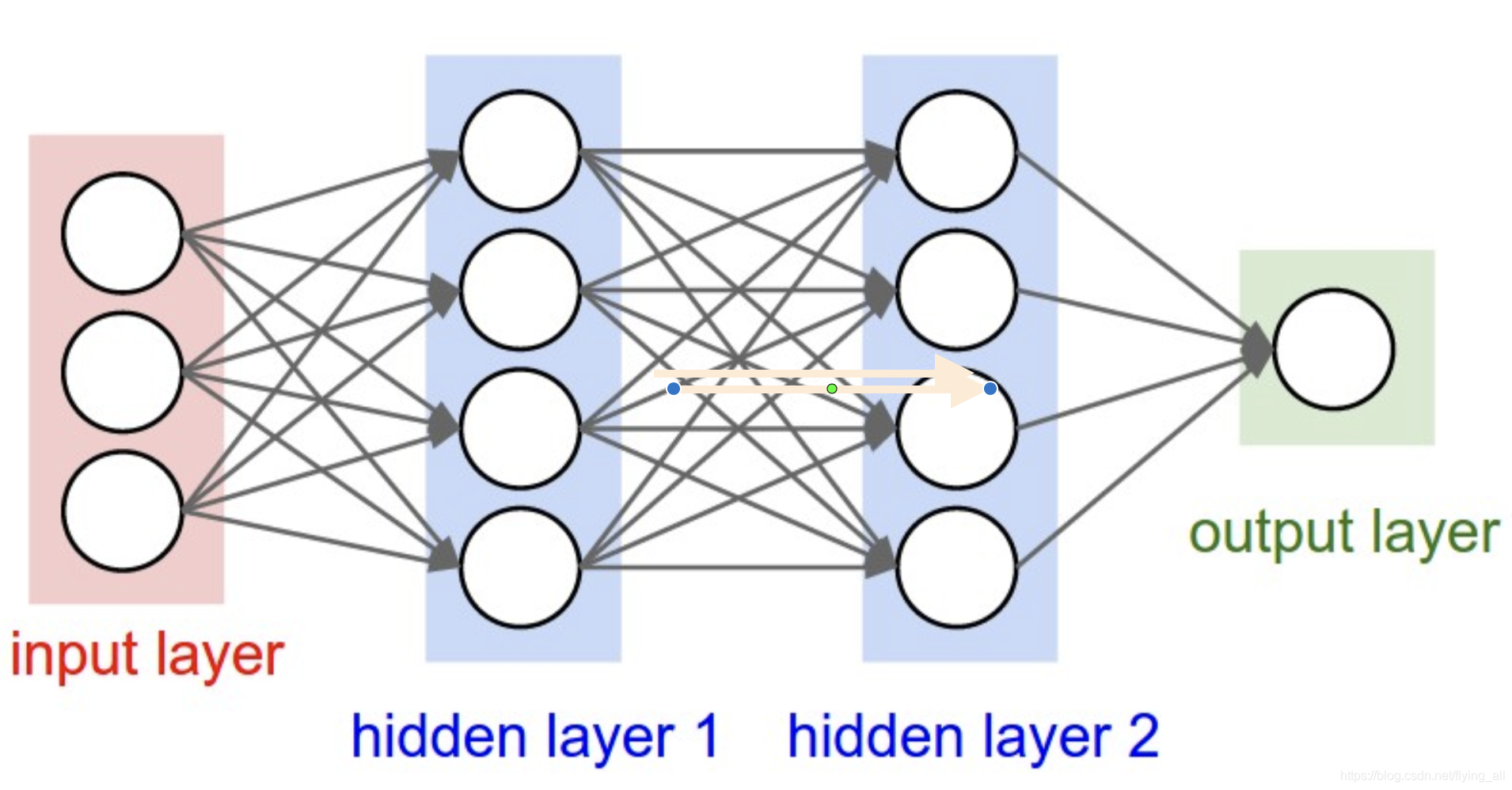
深度神经网络DNN是上面这个样子。前一层输出是后一层输入。每一层的输入输出是独立的。第n层的输出和第n+1层的输出是独立的，是没有关系的。CNN也一样。例如一张图像中要画出猫和狗的位置，那猫和狗是独立的，是用不同的神经元捕获特征。不会去根据猫的位置或者特征推测狗的位置。

但有些任务中后续的输出和之前的内容是有关系的。例如完形填空：我是中国人，我的母语是_____。RNN就是用来解决这类问题。

2 RNN的网络结构

2.1 RNN基础结构

RNN网络结构的特点是每一层网络执行相同的任务，但是输出依赖于输入和记忆。

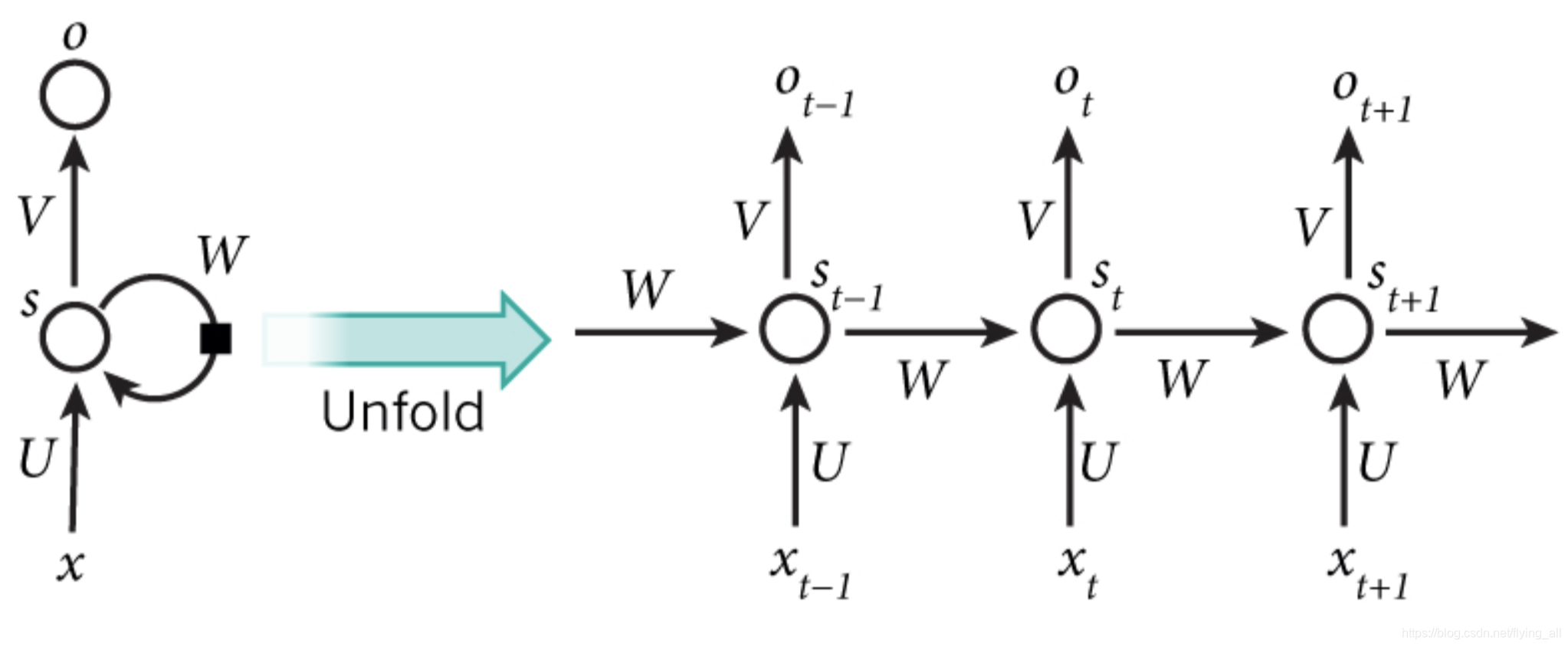
W,U,V是三个权重向量(是向量还是矩阵？),并且在所有网络层，值是相同的。
$x_t$是t时刻的输入
$S_t$是t时刻的记忆：$S_t=f(U{X}_t+W{S}_{t-1})$，f可以是tanh等函数，这个函数应该是一个值域范围固定的函数，例如函数范围在(-1,1)之间。这样可以保证神经网络不会爆炸
$O_t$是t时刻的输出，如果是输出下个词的话，那就是输出每个候选词的概率，$O_t=Softmax(V{S}_t)$

我们用高中学习的类比。如果t=高三，那么
W,U,V是我们的学习方法，高一，高二，高三这三年学习方法不变（在一轮迭代中）。
$x_t$是高三这一年老师教给我们的知识。
$S_t$是高三学习完以后能够记住的知识。我们能记住的知识取决于高二学习后能记住的知识$S_{t-1}$和高三这一年老师能交给我们的知识$x_t$。
$O_t$可以是高三毕业考试的成绩，它与高三学习完以后能够记住的知识有关。当然成绩是一个线性回归问题，与上面例子中说的多分类问题是两种类型的问题。

由于每一层共享参数W、U、V，所以RNN的参数量与CNN相比，是比较小的。
在有些问题中不一定有$O_t$。例如情感分类的任务中，只需要在读完所有句子，也就是最后一个时刻输出情感类别即可，过程中不需要。
$S_t$并不能捕捉所有时刻的信息，$S_t$是一个矩阵，能够存储的信息是有限的。

示例代码：唐诗生成器

2.2 不同类型的RNN

1 深层双向RNN

在有些情况下，当前的输出不仅依赖于之前序列的元素，还与之后的元素有关。例如在句法解析中。“He said, Teddy bears are on sale” and “He said, Teddy Roosevelt was a great President。在上面的两句话中，当我们看到“Teddy”和前两个词“He said”的时候，我们有可能无法理解这个句子是指President还是Teddy bears。因此，为了解决这种歧义性，我们需要往后查找。

${\vec{S}}_t=f(\vec{W}{x}_t+\vec{V}{\vec{S}}_{t-1}+\vec{b})$
${\overleftarrow{S}}_t=f\left(\overleftarrow{W}{x}_t+\overleftarrow{V}{\overleftarrow{S}}_{t+1}+\overleftarrow{b}\right)$
$y_t=g\left(U\left[{\vec{S}}_t;{\overleftarrow{S}}_t\right]+c\right)$

从左向右计算记忆${\vec{S}}_t$，从右向左计算记忆${\overleftarrow{S}}_t$，$U\left[{\vec{S}}_t;{\overleftarrow{S}}_t\right]$是对两个矩阵做拼接。

2 深层双向RNN

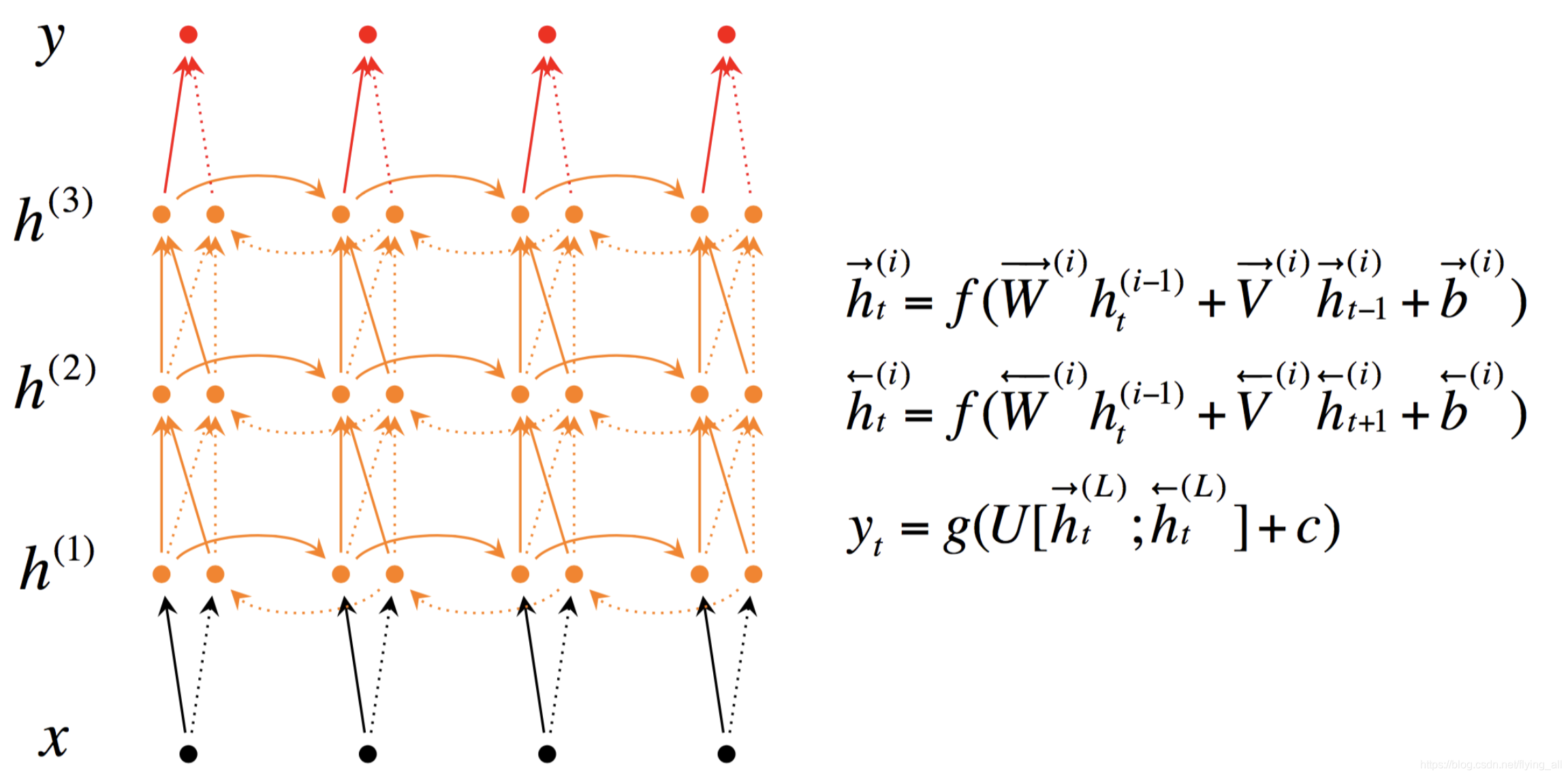
图中的h和之前的S是等价的。
这样的网络是说在每个时刻不仅学习一遍，可以学习3遍甚至更多。类比于，你读了三遍高一，三遍高二，三遍高三。

3 RNN的优化算法BPTT

BPTT和BP很类似，是一个思路，但是因为这里和时刻有关系。

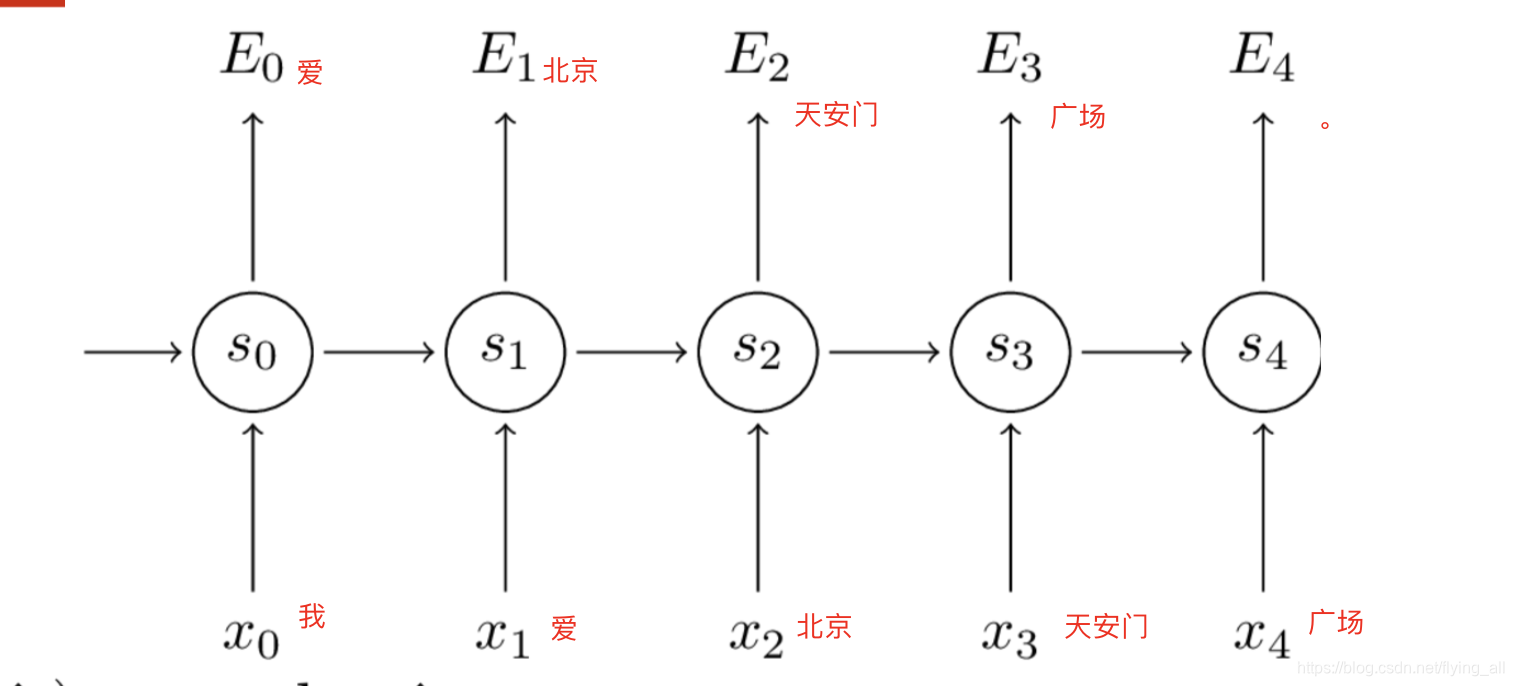
在这样一个多分类器中，损失函数是一个交叉熵。
某一时刻的损失函数是：$E_t\left(y_t,{\hat{y}}_t\right)=-y_t\log {\hat{y}}_t$
最终的损失函数是所有时刻的交叉熵相加：$$\begin{array}{rl}E(y,\hat{y})& =\sum _t{E}_t\left(y_t,{\hat{y}}_t\right)\\ & =-\sum y_t\log {\hat{y}}_t\end{array}$$

损失函数对W求偏导：$\frac{\partial E}{\partial W}={\sum }_t\frac{\partial E_t}{\partial W}$

假设t=3，$\frac{\partial E_3}{\partial W}=\frac{\partial E_3}{\partial {\hat{y}}_3}\frac{\partial {\hat{y}}_3}{\partial s_3}\frac{\partial s_3}{\partial W}$
$E_3$和$y_3$有关系，$y_3$和$s_3$有关系（参考2.1中的公式）。
而$s_3=tanh(U{x}_3+W{s}_2)$，$s_3$和$s_2$有关系，我们对$s_3$对W求偏导不能直接等于$s_2$，因为$s_2$也和W有关系。
$s_2=tanh(U{x}_2+W{s}_1)$

$s_2$和$s_1$有关系…一直到0时刻。所以我们会把每个时刻的相关梯度值相加：$$\frac{\partial s_3}{\partial W}=\sum _{k=0}^3\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}$$

至于这里为什么要把每个时刻的梯度相加可以参考文档，这里直接就是说相加。还有一些解释是：因为分子是向量，分母是矩阵，需要拆开来求导。或者根本上来讲是因为求导公式，我暂时没弄明白这一步。

其中我们在计算$\frac{\partial s_3}{\partial s_2}$的时候需要使用链式法则计算：$\frac{\partial s_3}{\partial s_1}=\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial s_1}\frac{\partial s_1}{\partial s_0}$

所以最终得到：$$\frac{\partial E_3}{\partial W}=\sum _{k=0}^3\frac{\partial E_3}{\partial {\hat{y}}_3}\frac{\partial {\hat{y}}_3}{\partial s_3}\frac{\partial s_3}{\partial s_k}\frac{\partial s_k}{\partial W}=\sum _{k=0}^3\frac{\partial E_3}{\partial {\hat{y}}_3}\frac{\partial {\hat{y}}_3}{\partial s_3}\left(\prod _{j=k+1}^3\frac{\partial s_j}{\partial s_{j-1}}\right)\frac{\partial s_k}{\partial W}$$

看公式中有连乘的部分。当使用tanh作为激活函数的时候，由于导数值分别在0到1之间，随着时间的累计，小于1的数不断相城，很容易趋近于0。(另外一种解释：如果权重矩阵 W的范数也不很大，那么经过 𝑡−𝑘 次传播后，$\frac{\partial s_3}{\partial s_k}$的范数会趋近于0，这也就导致了梯度消失。)

梯度消失带来的一个问题就是记忆力有限，离得越远的东西记住得越少。

4 LSTM

LSTM就是为了解决普通RNN中的梯度消失问题提出的。
LSTM提出了记忆细胞C，以及各种门。下图中的h与上面的S是相同含义，表示记忆。每个时刻的输出，在这里是没有画出来的。
假设现在有一个任务是根据已经读到的词，预测下一个词。例如输入法，生成诗词。

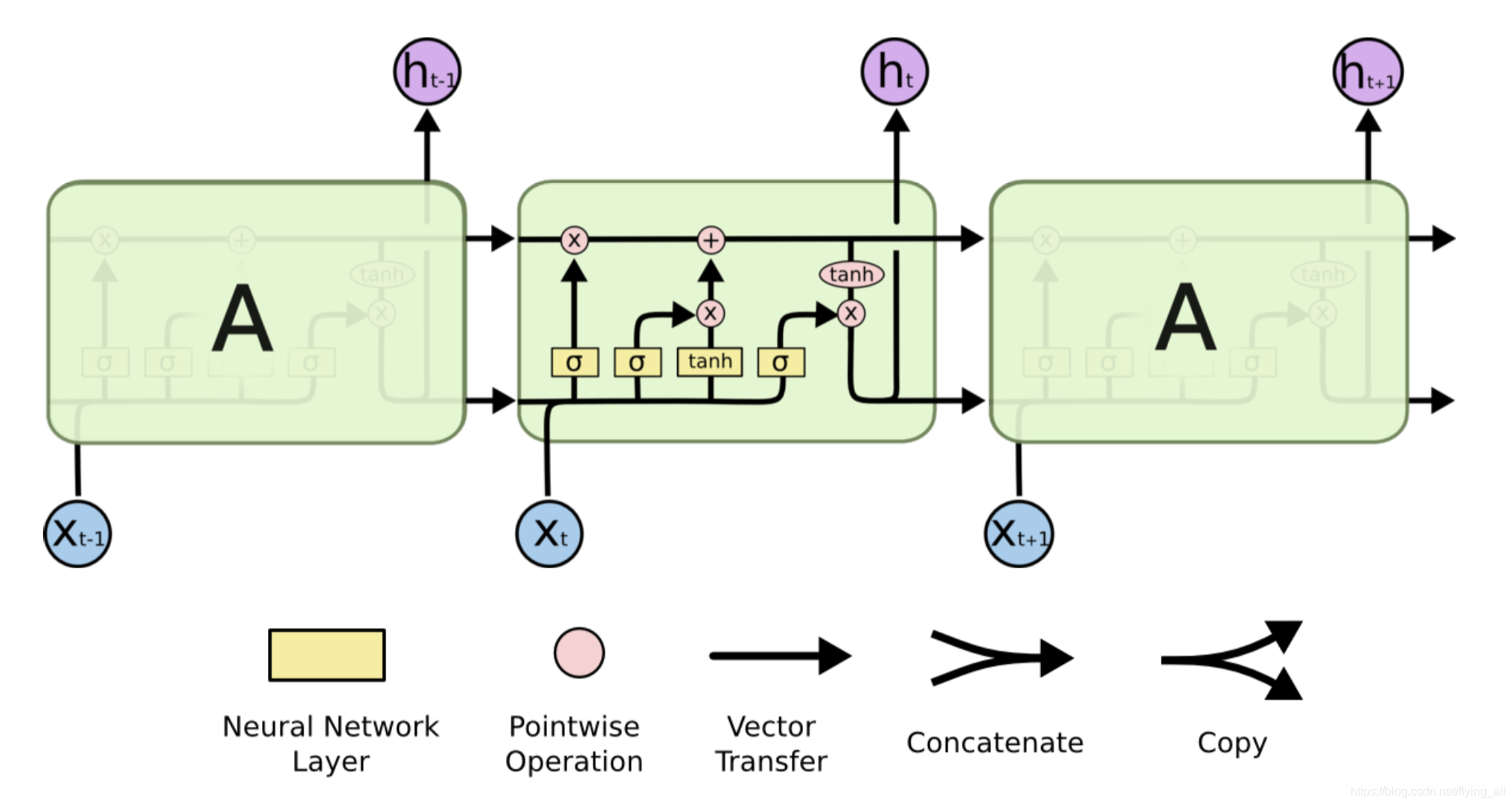
第1步：忘记门：从记忆细胞中丢弃一些信息

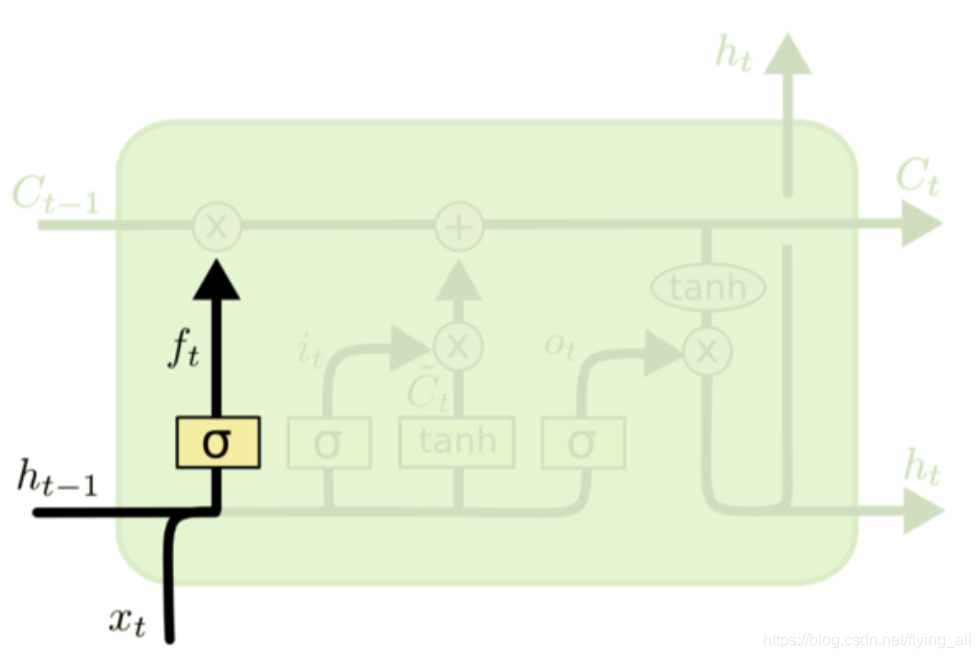
使用sigmoid函数，经过sigmoid之后得到一个概率值，描述每个部分有多少量可以通过。
$$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$$

如果C中包含当前对象的性别属性，现在已经正确的预测了当前的名词。当我们看到另外一个新的对象的时候，我们希望忘记旧对象的性别属性。

第2步：更新什么新信息到记忆中

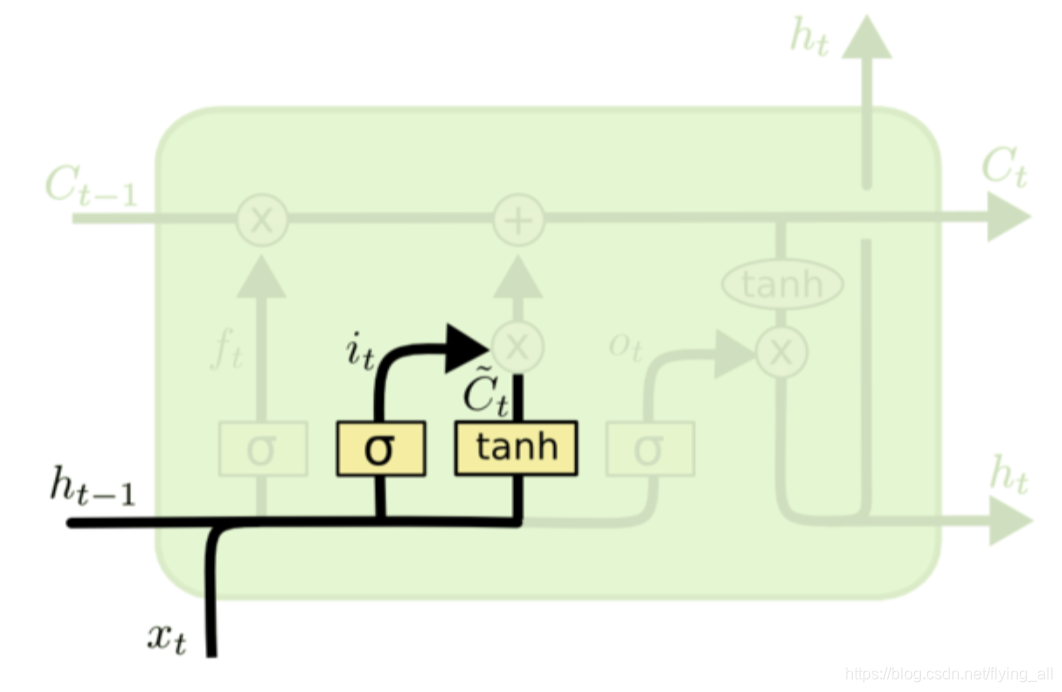
sigmoid决定什么值需要更新: $i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$
tanh层创建一个新的候选值向量（高三这一年学到的所有知识）： ${\tilde{C}}_t=\tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right)$

第3步：更新记忆细胞

把旧状态与$f_t$相乘，丢弃掉我们确定需要丢弃的信息；
加上$i_t$*${\tilde{C}}_t$,就是新的候选值，更新状态。
$$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$$
$C_{t-1}$是到高二以及之前的所有记忆，${\tilde{C}}_t$高三这一年学到的所有知识。带着两部分应该留下的内容去高考。

在任务中就是希望把新看到对象的性别属性添加到C，而把旧对象的性别属性删除。

第4步，基于细胞状态得到输出

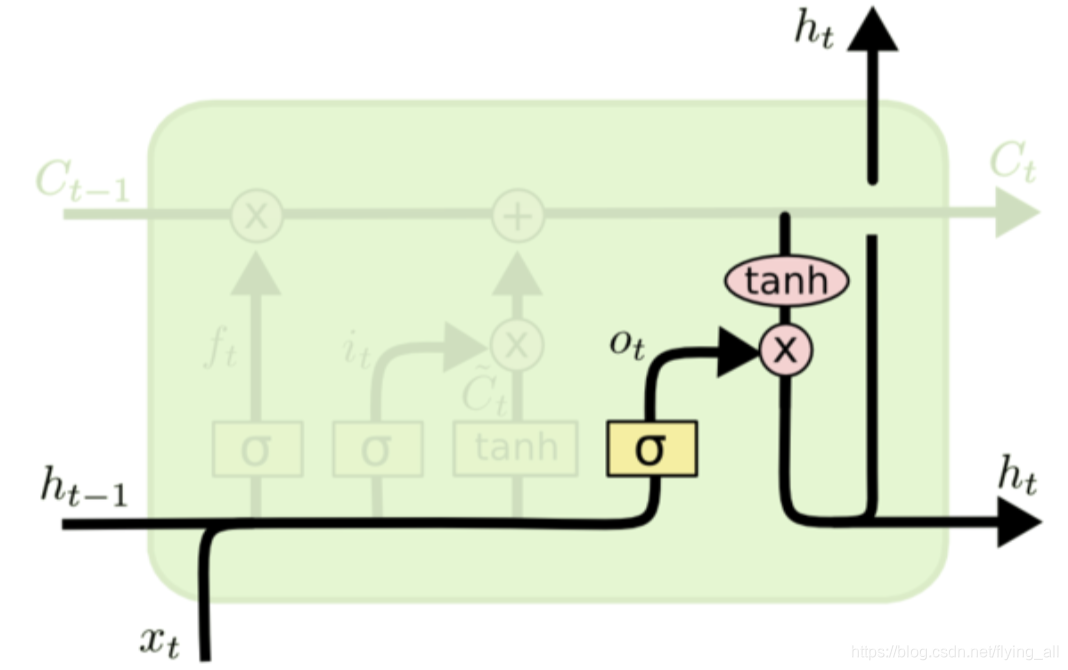
首先一个sigmoid层确定细胞状态的哪个部分的值将输出：$o_t=\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)$

接着用tanh处理细胞状态，输出我们确定输出的那部分，这部分是记忆用于下一时刻帮助做出决策的：$h_t=o_t\ast \tanh \left(C_t\right)$

在语言模型中，既然我当前看到了一个对象，这里可能输出一个动词信息，以备下一步需要用到。例如这里可能输出当前对象是单数还是复数，这样就知道下一个动词应该填写什么形式。

总结：

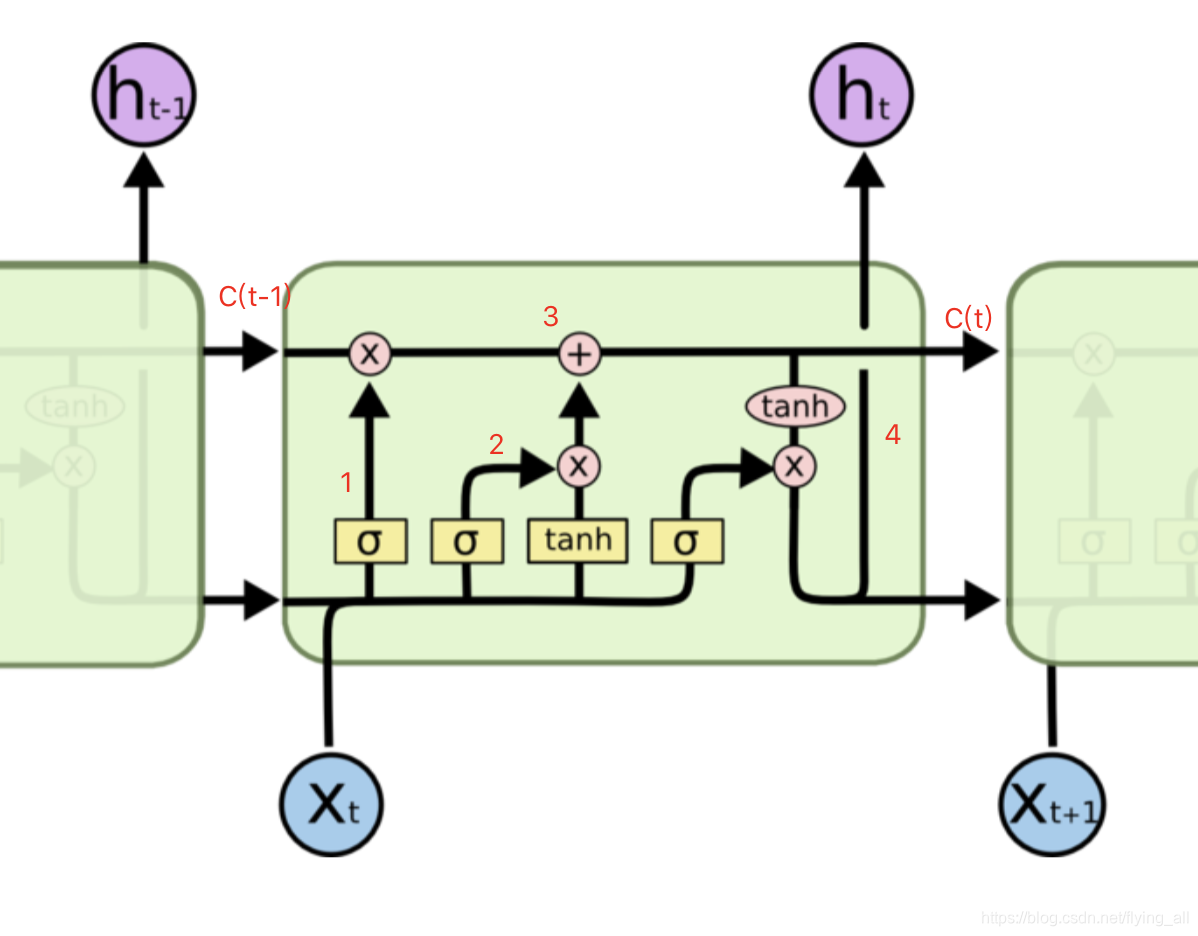
1：决定老细胞只留下哪部分$f_t=\sigma \left(W_f\cdot \left[h_{t-1},x_t\right]+b_f\right)$
2: 决定新知识应该记住哪部分:$i_t=\sigma \left(W_i\cdot \left[h_{t-1},x_t\right]+b_i\right)$
新学习到的知识：${\tilde{C}}_t=\tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right)$
3 更新细胞状态：$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t$
4 决定要输出哪部分：$o_t=\sigma \left(W_o\left[h_{t-1},x_t\right]+b_o\right)$
产生隐藏状态的输出：$h_t=o_t\ast \tanh \left(C_t\right)$

对比普通的RNN，输出$o_t=\sigma \left(V{S}_t\right)$,$S_t=tanh(U{x}_t+W{S}_{t-1})$，对于记忆$S_t$是由之前记忆和新知识共同组成。加入细胞状态可以选择忘记一部分老知识和选择忘记一部分新知识。

在之前的求导过程中$\frac{\partial s_3}{\partial s_1}=\frac{\partial s_3}{\partial s_2}\frac{\partial s_2}{\partial s_1}\frac{\partial s_1}{\partial s_0}$，现在变为。。。。。

输出$o_t=\sigma \left(V{h}_t\right)$
$h_t=o_t\ast \tanh \left(C_t\right)$
$C_t=f_t\ast C_{t-1}+i_t\ast {\tilde{C}}_t=f_t\ast C_{t-1}+i_t\ast \tanh \left(W_C\cdot \left[h_{t-1},x_t\right]+b_C\right)$
损失函数不变，还是令t=3，$\frac{\partial E_3}{\partial W}=\frac{\partial E_3}{\partial {\hat{y}}_3}\frac{\partial {\hat{y}}_3}{\partial h_3}\frac{\partial h_3}{\partial C_3}\frac{\partial C_3}{\partial W_c}$

要求$\frac{\partial C_3}{\partial W_c}$，这样$C_t$与$W_c$有关系，$C_{t-1}$与$W_c$有关系，两部分相加，对整个函数求导，就是对这两部分分别求导，再相加。与普通RNN的相乘
$\frac{\partial C_3}{\partial C_1}=\frac{\partial C_3}{\partial C_2}+\frac{\partial C_2}{\partial C_1}=?$

5 GRU

GRU是LSTM的变种之一。

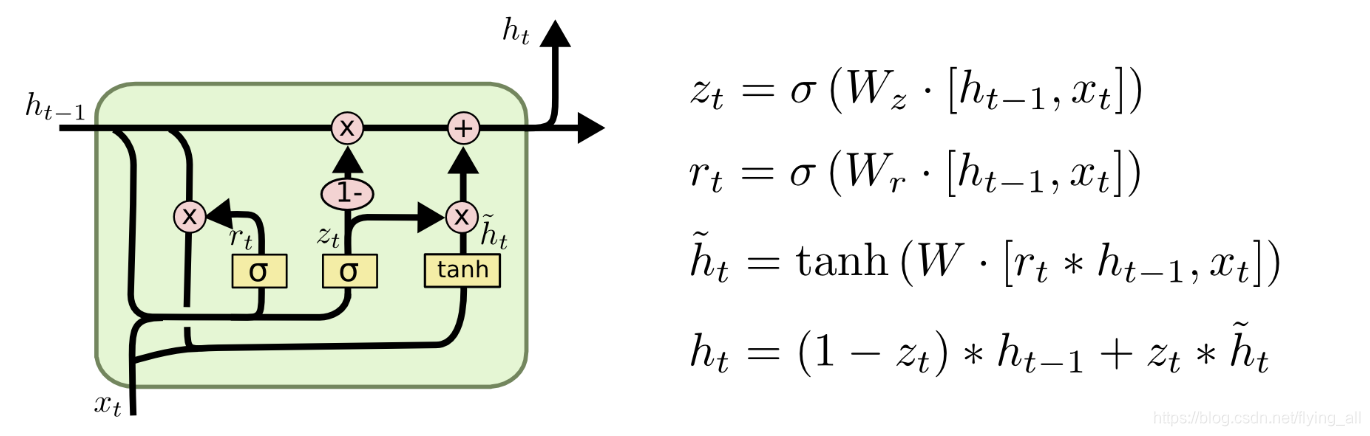
GRU做的改变是：
1 将忘记门和输入门合并成一个门，称为更新门。
2 细胞状态和隐藏状态，也就是上面的C和$h_t$合并为一个$h_t$。
这样GRU的参数就比标准LSTM要少，在很多情况下效果基本一致。