分享一下，后续持续更新中

1.思维建模

1.1 模型的用途

REDCAPE 推理（reason） 解释（explain）设计（design）沟通（communicate）行动（act）预测（predict）和探索（explore）

• 推理： 识别条件并推断逻辑含义；
• 解释： 为经验现象提供（可检验的）解释
• 设计： 选择制度，政策和规划的特征
• 沟通： 将知识与理解联系起来
• 行动： 指导政策选择和战略行动
• 预测： 对未来和未知现象进行数值和分类预测
• 探索：分析探索可能性和假说

1.2构建模型的3种方法

• 具身法（embodiment approch）
  包括重要部分，将不必要的部分进行剥离，或者将他们整合到一块。
• 类比法 ，对现实进行类比和抽象 ，类比法致力于刻画过程，系统或现象的本质。
• 实现法（alternative reality approach），这类模型可以作为分析和计算的“演练场”，我们可以利用这类模型探索各种各样的可能性。

1.3多样性预测定理

多模型误差 =平均模型误差-模型预测多样性

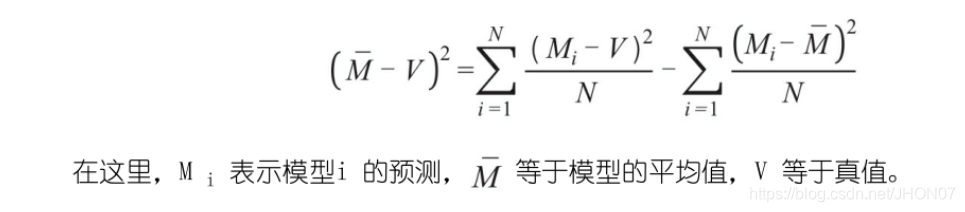
举例：
假设两个模型预测某一部电影会获得多少项奥斯卡奖。一个模型预测它将获得两项奥斯卡奖，另一个模型则预测获得8项目。这两个模型预测的平均值，就是5。如果最后这部电影获得了4项奥斯卡奖，那么第一个模型模型的误差等于（2-4）^2 即 4 第二个模型的误差等于（8-4）^2 即 16 而 多模型误差为 1

1.4分类模型

概念： 存在一组世界的对象或状态，每个对象或状态都由一组属性定义，每个属性都有一个值。
根据对象的属性，分类模型M 将对象或者状态划分为一个有限的类别集{S1，S2，…，Sn},然后给每个类别复制{M1，M2，…，Mn}

数据的维数限定了可以创建的模型数量。

1.5 变差模型

其中 ,V（x）等于X中x的值，$\overline{v}$ 等于平均值，M(x)等于模型的估值。
举例：

1.5.1 解释变差的百分比

1.6 模型误差分解定理

模型误差= 分类误差 +估值误差

1.7 多模型思维

• 一对多 (一个模型应用到多个领域)
  成功的一对多模型，取决于创造性的调整假设和构建新的类比，以便为某目的开发的模型，应用到新的领域中。（因此成为一个多模型思考者，不仅需要数学能力，更需要创造力）

1.8 对人类行为建模

1.8.1 理性行为者模式

行为者个体的偏好由一组，可能的行为定义的数学形式的，效用函数或收益函数（payoff function）来表示。行为个体选择函数值最大的行动。在博弈中，这种选择可能需要相信其他博弈这的行为。

• 证明效用函数存在的定理，需要假设一个备选的方案集确定偏好排序（即 函数设定存在的范围）。
• 偏好要与 效用函数一致，就必须满足完备性，传递性，独立性和连续性。一个具有注脚的文本。¹

选择行为者模型的理由

损失厌恶和双曲贴现

2.模型思维

2.1 正态分布

分布为事件或者价值分配概率。
衡量的方法：（1）均值 （2）方差

• 均值 各种统计量，将分布中的包含的信息压缩成单个数值。例如 均值 分布的平均值。
• 方差 第二个统计量，衡量一个分布的离散程度。

扩展 六西格玛（six sigma）
标准差，也称均方差，是各个数据偏离平均数的距离的平均数 。
举例：

2.2中心极限定理

只要各个变量，是相互独立的，每个随机变量贡献的方差，都是有限的，且没有任何一小部分随机变量，贡献了大部分方差，那 n>=20个随机变量的和就近似一个正态分布。

2.2.1 平方根法则

2.2.2 检验显著性

2.2.3 六西格玛

2.2 幂律分布

幂律分布就是常说的，长分布和尾分布
概念： 用数学表达式就是"节点的链接数和节点数的乘积是一个定值"
举例：

> 总结

首先的是问题归类，然后是数据建模，采用多个单模型，用不同的维度，来对问题进行分析；

参考：https://blog.csdn.net/weixin_44415209/article/details/108788867

---

1. 注脚的解释 ：参考：173页 ↩︎