应用背包问题：分享一下
有一个背包，容量是4磅，现有如下产品

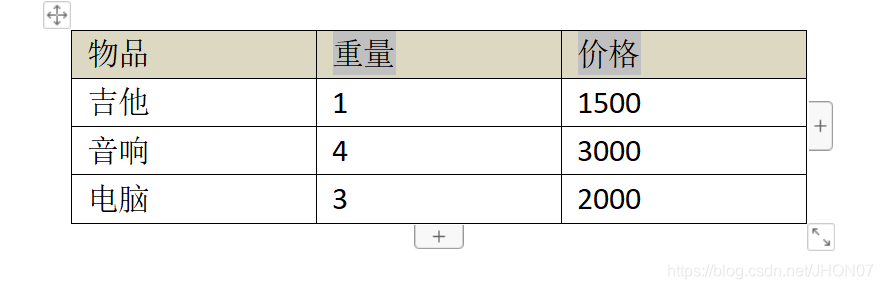
1)要求达到的目标为装入的背包的总价值最大，并且要求重量不能超出
2） 要求转入的物品不能重复

思路分析：算法其实是模型建立的过程

• 分析 建模的过程：
• 横向房物品的重量，从0~4磅
• 纵向是放的物品
  第一层，只能放一个吉他
  第二层，能放吉他和音响
  第三层，吉他，音响和电脑
• 依据建模过程，进行背包填表如下图：

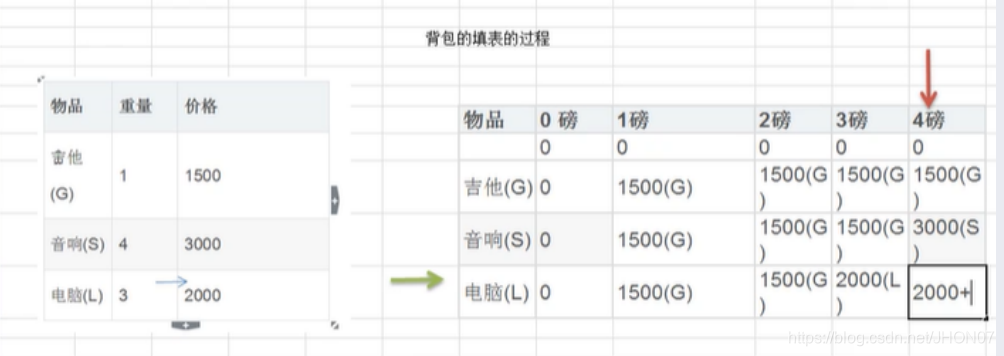
• 设计 一个二维数组，i 为行数表示第几行，j为列（表示装入的重量）如上图所示：设计第一行，和第一列为0 不放入任何东西；
• 声明 w[i] ，val[i] 分别表示 第i个物品的重量和价值
  w[i] 表示物品的重量 ，代码映射 int [] w={1,3,4},int[] val[]={1500,3000,2000}；
• int [][] v 变量存放 每个表格存放物品的最大价值
  分析得出模型
• 构建算法模型，注意考虑！临界条件（边界条件）
  条件 ：w[i]>j 时 v[i][j]= v[i-1][j]
  w[j]<=j 时 v[i][j] =max(v[i-1],v[i]+v[i-1][j-w[i]])
  算法的思想： 利用动态规划来解决，每次遍历第i个物品，根据 w[i],v[i] 来决定是否放入到背包中。01问题（只能添加一次，要么有，要么没有）

代码后续补上；
在这里插入代码片
下面展示一些 内联代码片。

package acm;/*** @author qxl*/
public class KnapsackProblem {public static void main(String[] args) {knapsack();}public static   void  knapsack(){// 背包的重量int [] w={1,4,3};//背包物品的价值int [] val={1500,3000,2000};//表格为4列int n=w.length;//表格有5列int m=val.length;int[][] v=new int[n+1][m+2];//表格初初始化,依据分析初始化 表格 第一行和第一列都为空// 二维数组 v.length  一维数组存放，每个行一维数组的地址for(int i=0;i<v.length;i++){v[i][0]=0;}// v[0].length 列数for(int i=0;i<v[0].length;i++){v[0][i]=0;}//遍历打印推演的价值表格for(int i=0;i<v.length;i++){for(int j=0;j<v[0].length;j++){System.out.print(v[i][j]+" ");}System.out.println();}// 分析出的模型： 当w[i]>j  v[i]=v[i-1][j] 注意！！理解 j-w[i] 求出 放入当前行物品后，剩余的重量；i-1 表示当前行上一行//  w[i]<=j   v[i]=max{v[i-1][j],v[i]+v[i-1][j-w[i]]}// O(n^2) 的时间复杂度//注意 第一行和第一列都为0 因此循环从第一个值开始for(int i=1;i<v.length;i++){//体现是思想，建模过程中涉及到的问题for(int j=1;j<v[0].length;j++){// 注意！！ w 和val 从下标1开始的，这里要注意了 都要进行 i-1;if(w[i-1]>j){v[i][j]=v[i-1][j];}else{// 由于遍历是从1开始的 因此 w[i]<=j 时候 v[i]= max{v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]}  其中注意！ val[i-1]// w[i-1] 主要是循环下标从1 开始的；v[i][j]= Math.max(v[i-1][j],val[i-1]+v[i-1][j-w[i-1]]);}}}//遍历打印推演的价值表格for(int i=0;i<v.length;i++){for(int j=0;j<v[0].length;j++){System.out.print(v[i][j]+"  ");}System.out.println();}}
}