在leetcode刷题过程中,遇到过很多关于排列组合的问题。弄清楚排列组合的相关原理,是非常有用处的。
文章目录
- 1 问题
- 2 排列-有序选取
- 2.1 重复选取-可重排列
- 2.2 不重复选取-排列
- 2.21 全排列
- 3 例题
- 4 总结
1 问题
设集合S包含n个元素,从S中选取r个元素有多少种选取方法?
根据取出的元素是否允许重复,以及取出元素的过程是否有序,可以将上述问题分为下面的四个子类型:

排列都是有序的,组合都是无序的。这在后面的学习中会深刻体会。
2 排列-有序选取
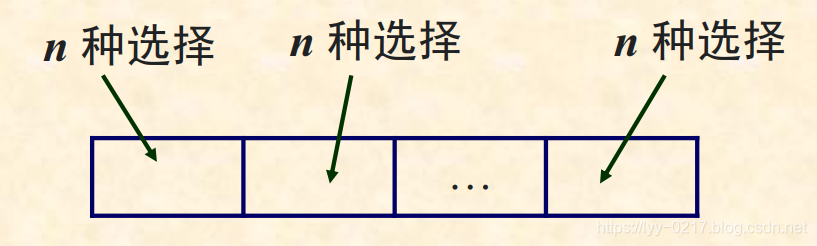
2.1 重复选取-可重排列
- 从 n 个不同的对象中, 取 r 个可重复的对象,按次序排列,称为n取r的可重排列。
- 此也即当 |A|=n 时, A* 中长为 r 的串的个数。
定理1:n取r的可重排列数目为nr
2.2 不重复选取-排列
-
从 n 个不同的对象中, 取 r 个不重复的对象, 按次序排列, 称为 n 取 r 的排列(permutation of n objects taken r at atime) 。 n 取 r 排列的全体构成的集合用 P(n, r) 表示, 排列的个数用 P(n, r) 表示(由于个数的表示是斜体不容易区分,后面我们说P(n, r) 即代表排列的个数。)
-
当 r = n 时称为全排列或置换(permutation)
-
此也即当 |A|=n 时, A* 中长为 r 且各项彼此不同的串的个数。
举例子:
- A = { a, b, c, d }, A 上的所有4取3的排列是:

- A = { a, b, c, d },A 上的所有全排列是:

定理2:
n < r 时, P(n, r) = 0;
n >= r 时, P(n, r) = n*(n - 1) * … *(n - r + 1)。

2.21 全排列
全排列经常被理解为是包含某个有限集合中的所有元素一次且仅一次的序列。
-
设 A 是集合,如果|A|=n, 则 A 的全排列的个数为:
n * (n-1) * … * 1
这个值也经常被写作 n! ,称作n 的阶乘(factorial) 。
可以给出 P(n, r) 的一个更紧凑的表达式:
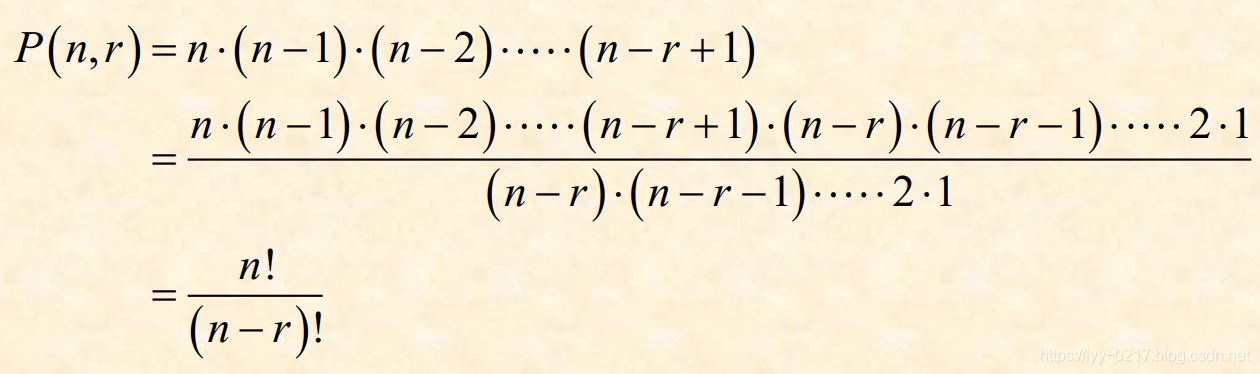
3 例题
- 例一
一个社团共有 10 名成员,从中选出一名主席、一名副主席、一名书记,则共有 P(10, 3)=720 种方法。(因为不光是要选出三名学生,还要在这三明学生中确定三个身份。相当于C(10,3)* P(3,3)=p(10,3),这样更易于理解。C(10,3)是组合的求解公式,后面会学习)
- 例二
如果有4个男孩和4个女孩坐成一排,每个人的旁边都可以随便坐,那么共有多少种坐的方式?
P(8,8)=8!
- 例三
如果有4个男孩和4个女孩坐成一排,每个人旁边都只能坐着异性,那么共有多少种坐的方式?
2 * 4! * 4!
如下图所示:

4 总结
- 坚持学数学