1>算法概述
KNN: 全名K-NearestNeighbor,K近邻算法,简单讲就是每个样本都可以用最接近的k个邻居表示,或者说共享同一个标签。KNN是一种分类(classification)算法,它输入基于实例的学习(instance-based learning),属于懒惰学习(lazy learning),也就是说没有学习过程,而是事先就已经准备好分类和特征值,可以直接对新样本进行处理分类。
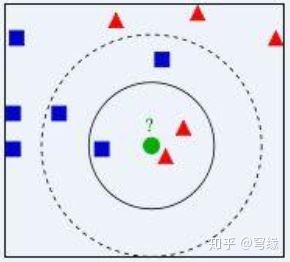
如图所示,绿点为测试样本,我们需要判断它是属于红色标签还是蓝色标签(r/b)。如果k=1,r:b = 2:1,测试样本为红色;如果k=2,r:b=2:3,测试样本为蓝色; 如果k=3,r:b=6:5,测试样本为红色。很显然k的取值对样本影响重大,下文将提及k值选取。
2>算法流程
1)计算测试数据与各个训练数据之间的距离;
2)按照距离的递增关系进行排序;
3)选取距离最小的K个点;
4)确定前K个点所在类别的出现频率;
5)返回前K个点中出现频率最高的类别作为测试数据的预测分类
3>算法实现
3.1准备数据

#scatter详解链接如下:
CSDN-专业IT技术社区-登录

数据可视化后生成的图如上,其中横轴是肿块大小,纵轴是发现时间。每个点代表不同病人的肿瘤大小和发病时间,根据颜色判断肿瘤是良性还是恶性。
现给出测试样本,判断点x = [8.90933607318, 3.365731514]属于哪种情况。
3.2计算距离
距离可以采用欧氏距离或马氏距离计算,此处采用欧几里得距离计算。
√(∑_(i=1)^n▒(x_i-y_i )^2 )

使用函数argsort对数组distances进行排序,距离由近到远,返回值为索引。

3.3选取k值
k值选取要适宜,k过大会导致模型简化而失去意义,k值过小则会将模型复杂化并产生过拟合现象。且k最好为奇数,以免出现结果相等的尴尬情况。
在实际应用中,K值一般取一个比较小的数值,例如采用交叉验证法(简单来说,就是一部分样本做训练集,一部分做测试集)来选择最优的K值。有点复杂,此处跳过。
暂且选择k值为6,找出最近的6个点,并记录他们的标签值。

3.3决策
统计所选点的标签,得到多的一个标签值是多少,即为测试点x的标签。

输出一个字典,“:”前面是数组中的值,后面是统计的数量;我们可以用most_common()方法找出预测值。

至此我们得到了测试点x的标签值为1。
4>自实现完整工程代码

5>算法优缺点
KNN的主要优点有:
- 理论成熟,思想简单,既可以用来做分类也可以用来做回归
- 天然解决多分类问题,也可用于回归问题
- 和朴素贝叶斯之类的算法比,对数据没有假设,准确度高,对异常点不敏感
- 由于KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的,因此对于类域的交叉或重叠较多的待分样本集来说,KNN方法较其他方法更为适合
KNN的主要缺点有:
- 计算量大,效率低。即使优化算法,效率也不高。
- 高度数据相关,样本不平衡的时候,对稀有类别的预测准确率低
- 相比决策树模型,KNN模型可解释性不强
- 维度灾难:随着维度的增加,“看似相近”的两个点之间的距离越来越大,而knn非常依赖距离
#参考链接:
机器学习的敲门砖:kNN算法(上)mp.weixin.qq.com