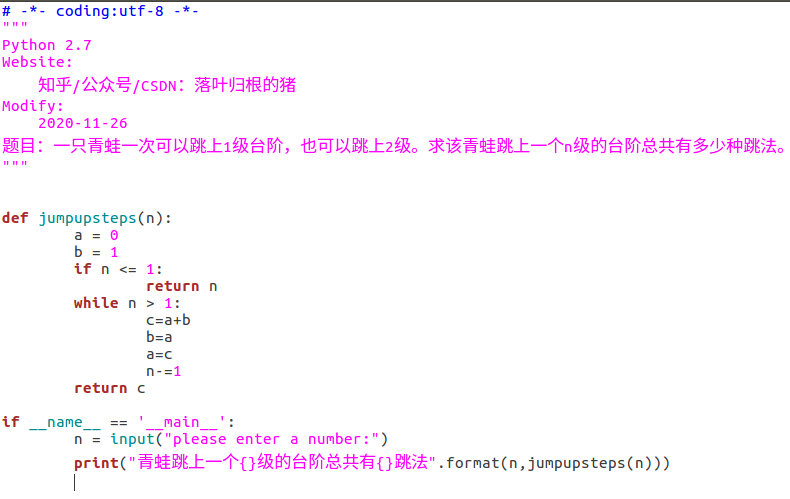
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
1. 思路:
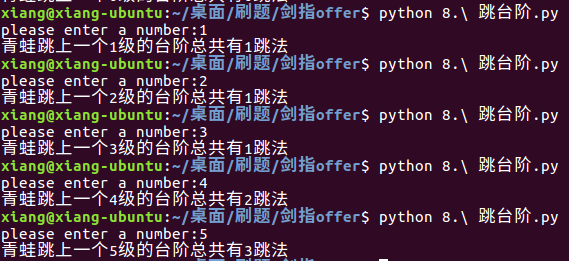
若只有一级台阶:一种跳法
两级台阶:两种跳法(1+1 / 2)
三级台阶:三种跳法(1+1+1 / 1+2 / 2+1)
四级台阶:五种跳法:1+1+1+1 / 1+1+2 / 1+2+1 / 2+1+1 / 2+2
我们来讨论一般情况。我们把n级台阶时的跳法看成是n的函数,记为f(n)。当n>2时,第一次跳的时候就有两种不同的选择:一是第一次只跳1级,此时跳法数目等于后面剩下的n-1级台阶的跳法数目,即为f(n-1);另外一种选择是跳一次跳2级,此时跳法数目等于后面剩下的n-2级台阶的跳法数目,即为f(n-2)。因此n级台阶的不同跳法的总数f(n)=f(n-1)+f(n-2)。分析到这里,我们不难看出这实际上就是斐波那契数列了。

推荐阅读:
★ 求职经验:点这里
★ 算法刷题:点这里
★ 投资理财:点这里
★ AI很简单:
★ 扫盲科普:点这里
♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠♥◆♣♠