1

力的合成

一、合力与分力

       当一个物体受到几个力的共同作用时，我们常常可以求出这样一个力，这个力产生的效果跟原来几个力的共同效果相同，这个力就叫做那几个力的合力，原来的几个力叫做分力．

二、合力与分力的关系

       1.合力与分力之间的关系是一种等效替代的关系，合力作用的效果与分力共同作用的效果相同．

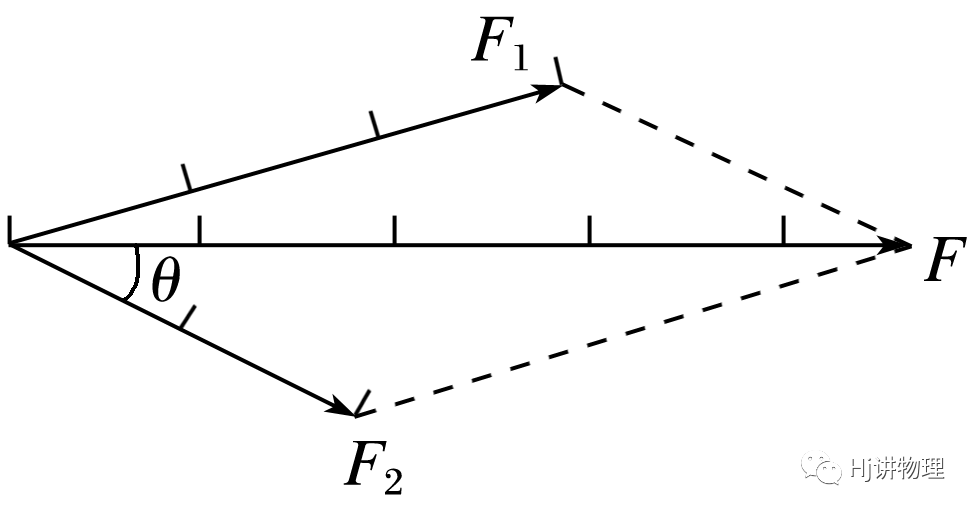
       2.两分力大小不变时，合力F随两分力F1、F2夹角θ的增大而减小，随θ的减小而增大.(0°≤θ≤180°)

      (1)两分力同向(θ＝0°)时，合力最大，F＝F1＋F2，合力与分力同向.

     (2)两分力反向(θ＝180°)时，合力最小，F＝|F1－F2|，合力的方向与较大的一个分力的方向相同.

       (3)合力的取值范围：|F1－F2|≤F≤F1＋F2.

      3.合力可能大于某一分力，可能小于某一分力，也可能等于某一分力.

三、力的合成

      1.定义：求几个力的合力的过程叫做力的合成．

      2.矢量相加的法则

      ①矢量：既有大小，又有方向，合成时遵守平行四边形定则或三角形定则的物理量．

      ②标量：只有大小，没有方向，求和时按照算术法则相加的物理量．

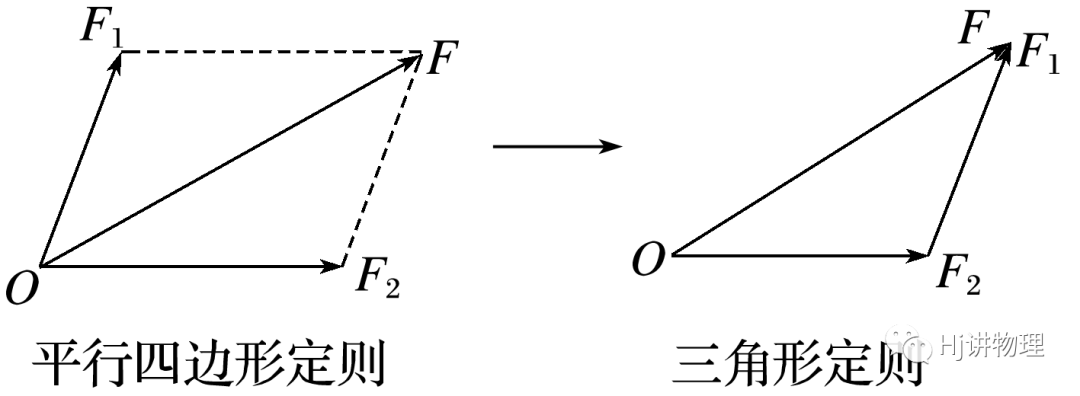
      ③平行四边形定则：两个力合成时，以表示这两个力的线段为邻边作平行四边形，这两个邻边之间的对角线就代表合力的大小和方向．

      ④三角形定则：把两个矢量首尾相接，从第一个矢量的始端指向第二个矢量的末端的有向线段就表示合矢量的大小和方向．三角形定则与平行四边形定则实质上是一样的．

      3.合力的求解

      (1)作图法

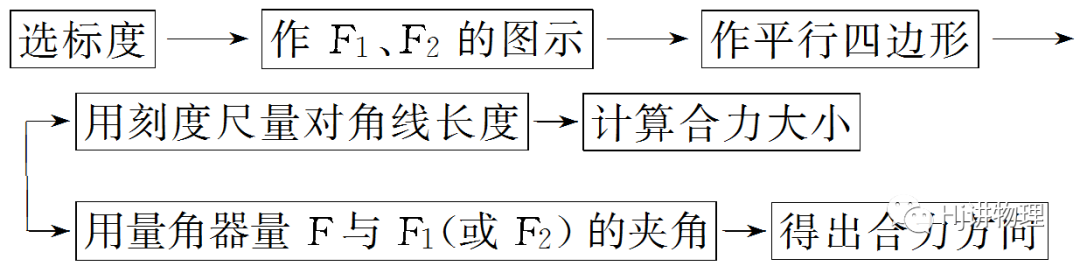
      (2)计算法

       a.两分力共线时：

      ①若F1、F2两力同向，则合力F＝F1＋F2，方向与两力同向．

     ②若F1、F2两力反向，则合力F＝|F1－F2|，方向与两力中较大的同向．

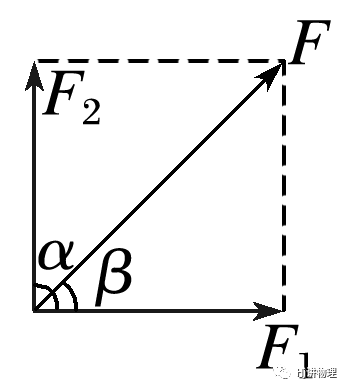
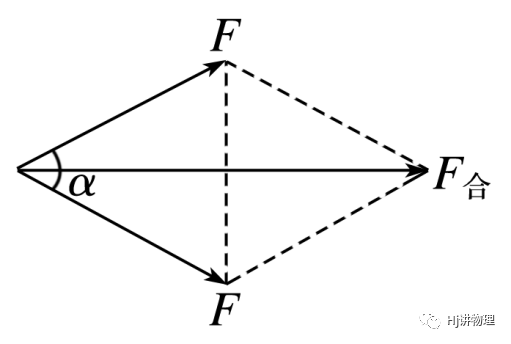
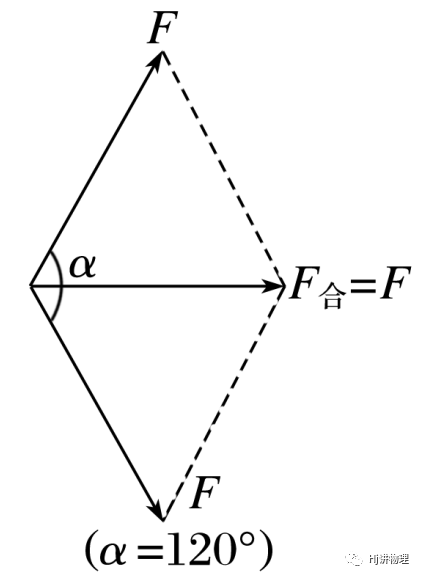
       b.两分力不共线时：

      可以根据平行四边形定则作出力的示意图，然后由几何关系求解对角线，其长度即为合力大小．以下为两种特殊情况：

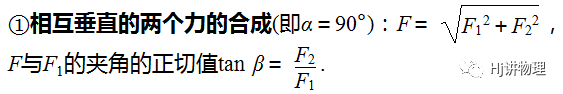
四、多力的合成

      1．合成方法：多个力的合成的基本方法仍是平行四边形定则．具体做法是先任选两个分力求出它们的合力，用求得的结果再与第三个分力求合力，直到将所有分力的合力求完．

      2．三个力合力范围的确定

     (1)最大值：三个力方向均相同时，三力合力最大，Fm＝F1＋F2＋F3.

     (2)最小值

      ①若一个力在另外两个力的和与差之间，则它们的合力的最小值为零．

      ②若一个力不在另外两个力的和与差之间，则它们的合力的最小值等于三个力中最大的力减去另外两个力．

五、共点力

      1．定义：如果几个力共同作用在同一点上，或者虽不作用在同一点上，但它们的延长线交于一点，这样的一组力叫做共点力．

       2．力的合成的平行四边形定则，只适用于共点力．

2

力的分解

一、定义：已知一个力求它的分力的过程．

二、分解原则

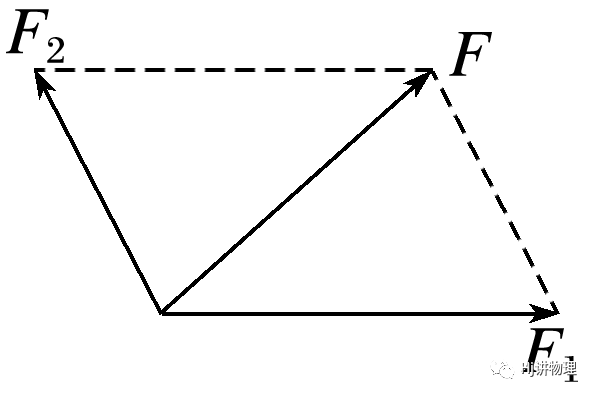
      1.力的分解是力的合成的逆运算，同样遵守平行四边形定则．

      2.把一个已知力F作为平行四边形的对角线，与力F共点的平行四边形的两个邻边，就表示力F的两个分力F1和F2.

三、力的分解方法

      1.一个力可以分解为两个力，若没有限制，同一个力可以分解为无数对大小、方向不同的分力．也可以说，如果没有限制，对于同一条对角线，可以作出无数个不同的平行四边形．

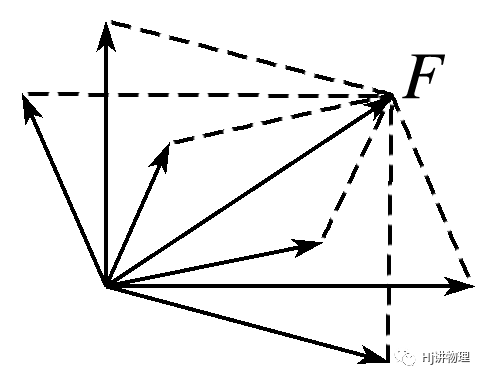
       2.力的分解问题的关键是根据力的作用效果分解，解题常用思路为

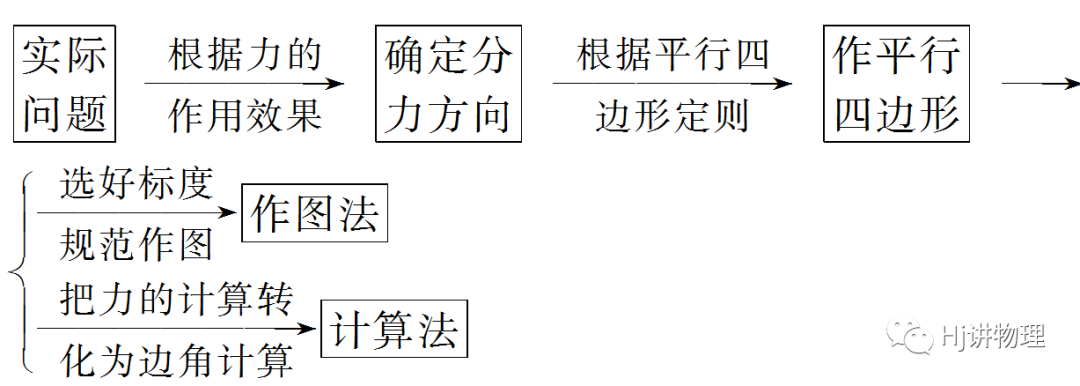
总结提升

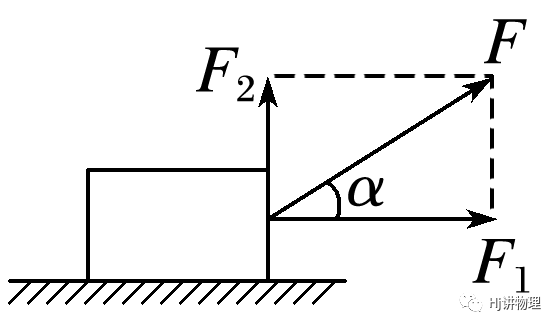
       1.水平地面上物体受斜向上的拉力F，拉力F一方面使物体沿水平地面前进，另一方面向上提物体，因此拉力F可分解为水平向前的力F1和竖直向上的力F2.F1＝Fcosα，F2＝Fsinα.

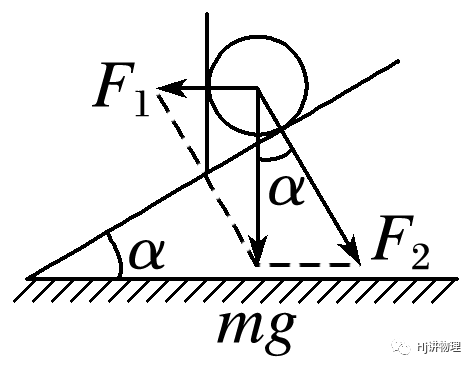
      2.质量为m的物体静止在斜面上，其重力产生两个效果：一是使物体具有沿斜面下滑趋势，二是使物体压紧斜面．因此重力可分解为沿斜面的分力F1和垂直于斜面的分力F2.F1＝mgsinα，F2＝mgcosα.

      3.质量为m的光滑小球被竖直挡板挡住而静止于斜面上时，其重力产生两个效果：一是使球压紧挡板，二是使球压紧斜面．因此重力可以分解为垂直于挡板的分力F1和垂直于斜面的分力F2.F1＝mgtanα，F2＝mg/cosα.

      4.质量为m的光滑小球被悬线挂靠在竖直墙壁上，其重力产生两个效果：一是使球压紧竖直墙壁，二是使球拉紧悬线．因此重力可以分解为垂直于墙壁的分力F1和沿着绳的分力F2.F1＝mgtanα，F2＝mg/cosα.

      5.A、B两点位于同一平面上，质量为m的物体被AO、BO两线拉住，其重力产生两个效果：一是使物体拉紧AO线，二是使物体拉紧BO线．因此重力可以分解为沿AO线的分力F1和沿BO线的分力F2.F1＝F2＝mg/2sinα.

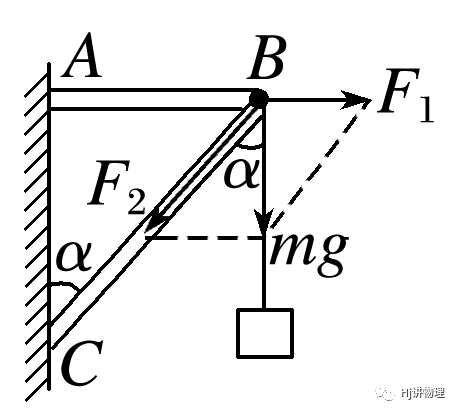
      6.质量为m的物体被支架悬挂而静止，其重力产生两个效果：一是拉伸AB，二是压缩BC.因此重力可以分解为沿AB的分力F1和沿BC的分力F2.F1＝mgtanα，F2＝mg/cosα.

      7.有限制条件的力的分解

      力分解成互成角度的两个分力，有解或无解，简单地说就是代表合力的对角线与给定的代表分力的有向线段是否能构成平行四边形(或三角形)．若可以构成平行四边形(或三角形)，说明合力可以分解成给定的分力，即有解；若不能，则无解．常见的有以下几种情况：

      已知两个分力的方向——唯一解

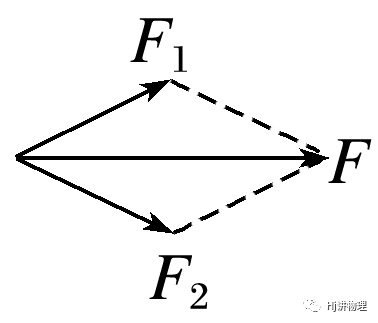
      已知一个分力的大小和方向——唯一解

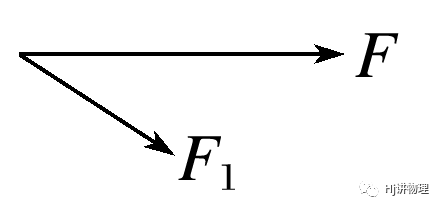
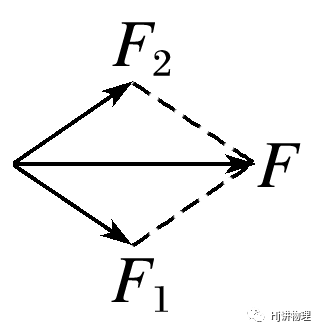
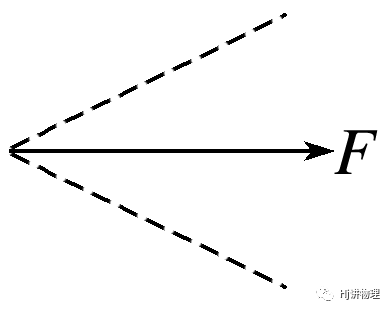
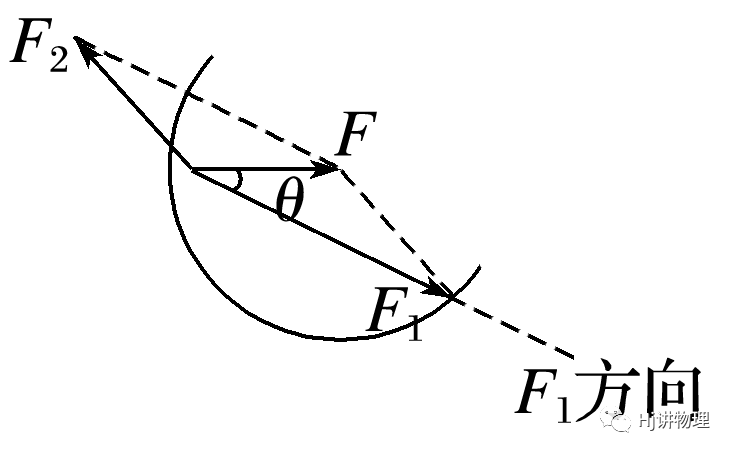
      已知一个分力(F2)的大小和另一个分力(F1)的方向

      ①F2＜Fsinθ——无解

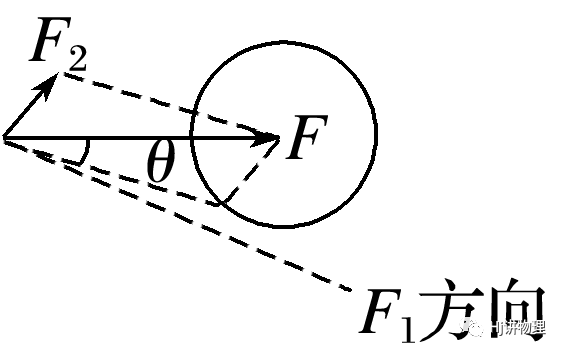
      ②F2＝Fsinθ——唯一解

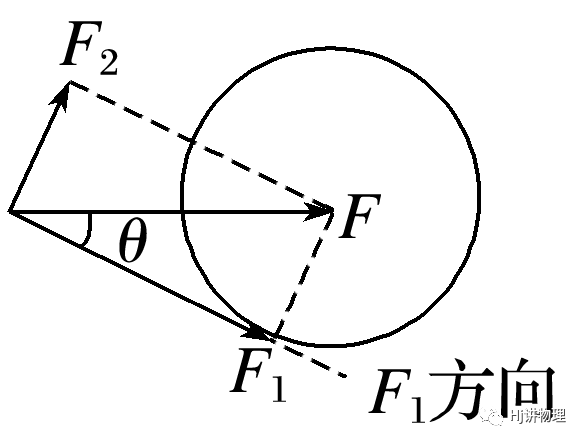
      ③Fsinθ＜F2＜F——两解

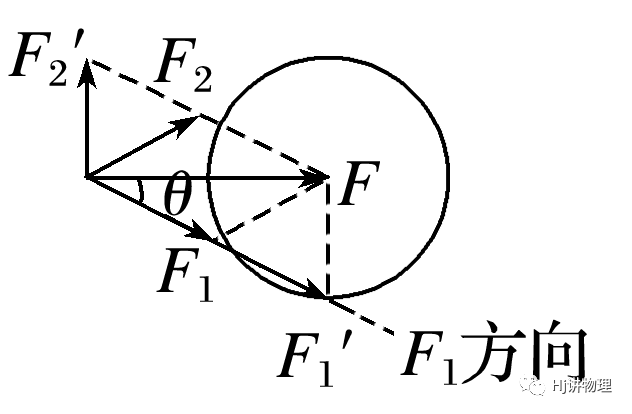
      ④F2≥F——唯一解

四、力的正交分解法

      1．力的正交分解法：把力沿着两个选定的相互垂直的方向分解的方法．

      2．正交分解法求合力的步骤：

      (1)建立直角坐标系：以共点力的作用点为坐标原点，直角坐标系x轴和y轴的选择应使尽量多的力在坐标轴上．

      (2)正交分解各力：将每一个不在坐标轴上的力分解到x轴和y轴上，并求出各分力的大小．

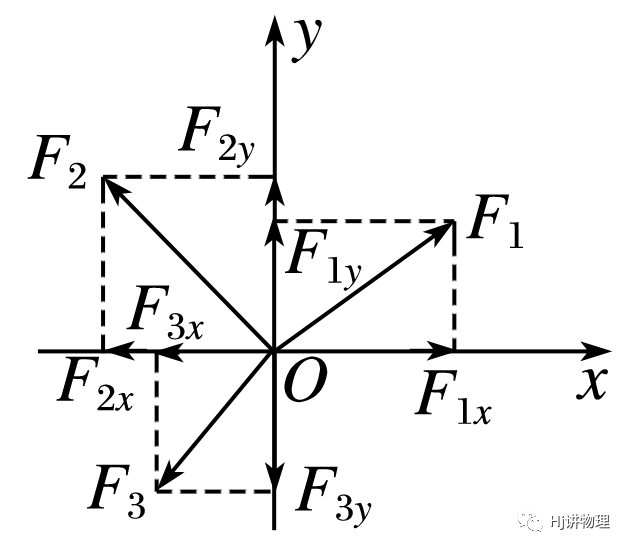
      (3)分别求出x轴、y轴上各分力的矢量和，即：Fx＝F1x＋F2x+…，Fy＝F1y＋F2y＋….

      1．坐标轴的选取原则：坐标轴的选取是任意的，为使问题简化，建立直角坐标系时坐标轴的选取一般有以下两个原则：

      (1)使尽量多的力处在坐标轴上．

      (2)尽量使某一轴上各分力的合力为零．

      2．正交分解法的适用情况：适用于计算物体受三个或三个以上共点力的合力情况．

扫码关注我哦！

微信号｜Hjjiangwuli

微信公众号｜Hj讲物理