matlab 矩阵jocobi迭代_第6章 解线性方程组的迭代法(基于MATLAB)

5f733c2f3e7d4e73c384edec5dff8eae.png

前面我们已经知道对于线性方程组，一般有两种数值解法：直接法和迭代法。直接法前面已经写过了，没看的同学可以移步阅读：直接法。本次主要讲述迭代法及其相应的MATLAB代码。

考虑线性方程组

当

为低阶稠密阵时一般采取直接法进行求解。但是我们在工程技术中经常遇到的是一些大型稀疏矩阵方程组(
的阶数很大，但
元素较多，解PDE(Partial Differential Equation)时常遇到)，此时利用迭代法进行求解是合适的。在计算机内存和运算两方面，迭代法通常都可利用
中有大量
元素的特点。

本文主要介绍迭代法的基本思路和雅可比(Jacobi)迭代法、高斯-塞德尔(Gauss-Seidel)迭代法、(逐次)超松弛(SOR, Successie over Relaxation)迭代法、共轭梯度(CG, Conjugate Gradient)法。

1. 迭代法的基本思路

对于线性方程组

为了使用迭代法对其进行求解，我们首先需要构造迭代序列，我们将上式改写为

其中

和
都是已知的，从而我们就可以构造出一个迭代序列为

对向量序列

一组初始值
，如果上述迭代序列收敛(有课本定理知其充要条件为
)，最终向量序列
将逐步逼近原方程组的精确解
。迭代次数越多，计算误差就越小，因此，任意给定一个精度，都可以通过迭代计算出满足精度要求的解(理论上，实际情况还需考虑计算机存储字长)。

这就是我们构造迭代法的基本思路。MATLAB代码为

function [x,t,it] = Iteration(A,b,I,eps)
% 输入：
% A: 系数矩阵
% b: 载荷矩阵
% I: 最大迭代次数
% 输出：
% x: 解矩阵
% t: 时间
% it: 迭代次数
% 迭代初值默认为 0if nargin < 4eps = 1e-6;
endtic
[n,~] = size(A);
B = zeros(size(A));
x = zeros(n,1);
f = zeros(n,1);for r = 1:nfor l = 1:nif l == rB(r,r) = 0;elseB(r,l) = -A(r,l)/A(r,r);endendf(r) = b(r)/A(r,r);
endx_exact = Ab;
it = 1;
for k = 1:I-1x = B*x+f;if norm(x-x_exact)>epsit = it+1;end
end
t = toc;
end

示例：

clear
A = [8 -3 2; 4 11 -1; 6 3 12]; b = [20; 33; 36];
I = 1000;
[x,t,it] = Iteration(A,b,I)

运行结果

x =321t =0.016490086000000it =16

可见只是迭代

次，就满足默认精度(
)。

2. 雅可比(Jacobi)迭代法

其实上面第1节的代码使用的方法就是最原始的雅可比迭代法，只是在形式上看起来不那么规范。下面我们来看规范的解

的雅可比迭代法的形式：

其中

，
，这里
分别为对角阵、下三角阵、上三角阵。并称
为解
的雅可比迭代法的迭代矩阵。

其分量计算公式为

但实际编程计算一般采取简洁且高效的矩阵形式，其MATLAB代码为

function [x,t,it] = Jacobi(A,b,I,eps)
% 雅可比迭代法
% 输入：
% A: 系数矩阵
% b: 载荷矩阵
% I: 最大迭代次数
% 输出：
% x: 解矩阵
% t: 时间
% it: 迭代次数
% 迭代初值默认为 0if nargin < 4eps = 1e-6;
endtic
[n,~] = size(A);
x = zeros(n,1);D = diag(diag(A)); %求 A 的对角矩阵
L = -tril(A,-1); %求 A 的下三角矩阵,不带对角线
U = -triu(A,1); %求 A 的上三角矩阵
J = D(L+U);
f = Db;x_exact = Ab;
it = 1;
for k = 1:I-1x = J*x+f;if norm(x-x_exact)>epsit = it+1;end
endt = toc;
end

仍然计算第一节的例子，只需把函数名改一下：

clear
A = [8 -3 2; 4 11 -1; 6 3 12]; b = [20; 33; 36];
I = 1000;
[x,t,it] = Jacobi(A,b,I)

运行结果也与第1节一致：

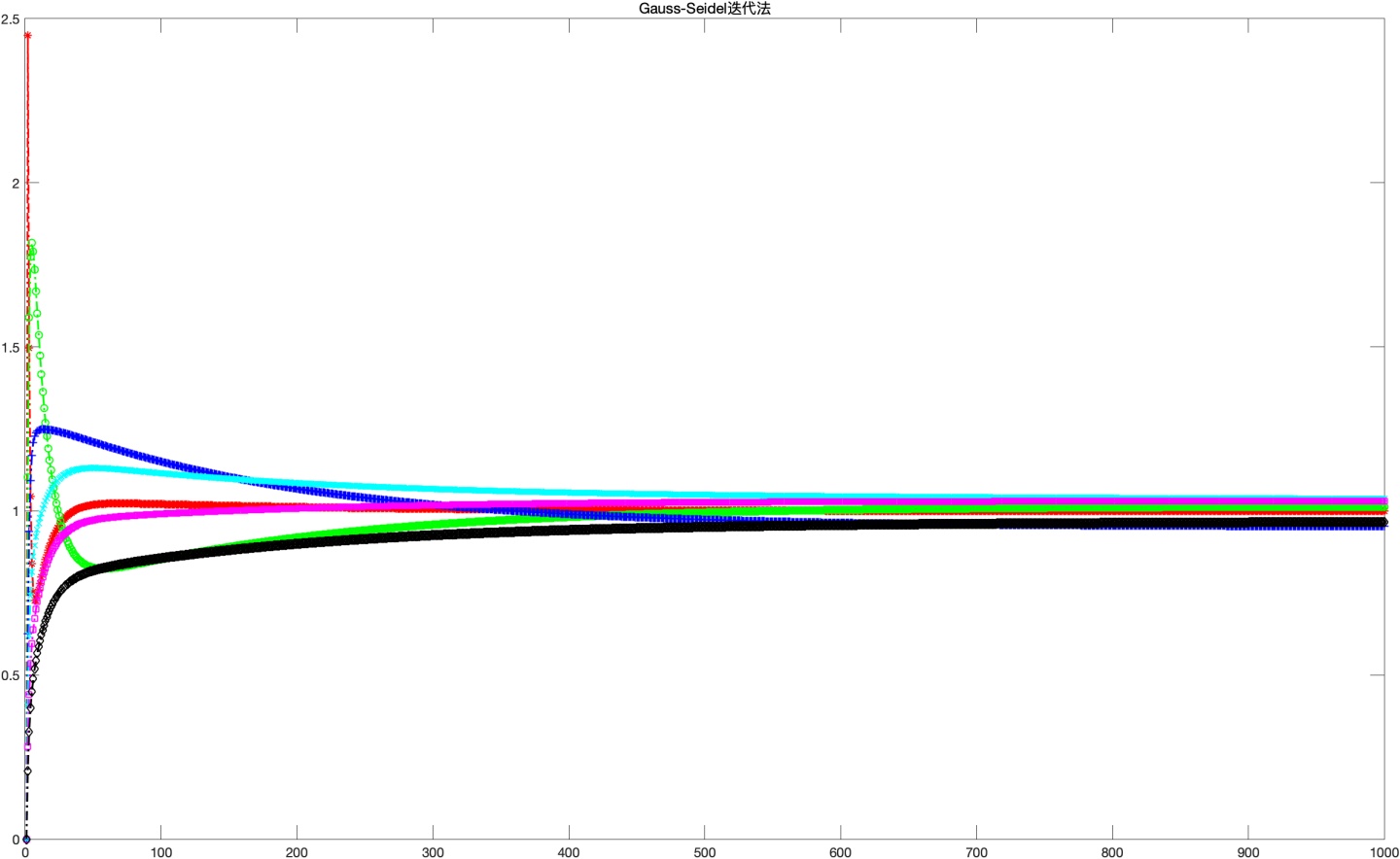
x =321t =0.037686548000000it =16

3. 高斯-塞德尔(Gauss-Seidel)迭代法

高斯-塞德尔迭代法与雅可比迭代法很相似，可以看成是其的一种改进。其形式为：

其中

，
，这里
分别为对角阵、下三角阵、上三角阵。并称
为解
的高斯-塞德尔迭代法的迭代矩阵。

其分量计算公式为

其MATLAB代码亦采取矩阵形式：

function [x,t,it] = GaussSeidel(A,b,I,eps)
% 高斯-赛德尔(Gauss-Seidel)迭代法
% 输入：
% A: 系数矩阵
% b: 载荷矩阵
% I: 最大迭代次数
% 输出：
% x: 解矩阵
% t: 时间
% it: 迭代次数
% 迭代初值默认为 0if nargin < 4eps = 1e-6;
endtic
[n,~] = size(A);
x = zeros(n,1);D = diag(diag(A)); %求 A 的对角矩阵
L = -tril(A,-1); %求 A 的下三角矩阵,不带对角线
U = -triu(A,1); %求 A 的上三角矩阵
G = (D-L)U;
f = (D-L)b;x_exact = Ab;
it = 1;
for k = 1:I-1x = G*x+f;if norm(x_exact-x)>epsit = it+1;end
endt = toc;
end

同样计算前面的例子，其结果为：

x =321t =0.054796674000000it =8

从结果可以看出，对于同样的精度要求，高斯-塞德尔迭代法只需要

次迭代(雅可比迭代法需要
次)，收敛明显要更快。

3. (逐次)超松弛(SOR)迭代法

简单来说，逐次超松弛迭代法就是在前面高斯-塞德尔迭代法的基础上加了松弛因子

，所以解
的SOR方法为

，初始向量，

其中

，
。

其分量计算公式为

显然，当

时，SOR方法即为高斯-塞德尔迭代法。当
时，称为
超松弛法；当
时，称为
低松弛法。

其MATLAB代码为

function [x,t,it,w] = SOR(A,b,I,eps,w)
% 逐次超松驰迭代法(successive over relaxation method)迭代法
% 输入：
% A: 系数矩阵
% b: 载荷矩阵
% I: 最大迭代次数
% w: 松弛因子(w=1 时即为 Gauss-Seidel 迭代法)
% 输出：
% x: 解矩阵
% t: 时间
% it: 迭代次数
% w: 松弛因子
% 迭代初值默认为 0tic
[n,~] = size(A);
x = zeros(n,1);D = diag(diag(A)); %求 A 的对角矩阵
L = -tril(A,-1); %求 A 的下三角矩阵,不带对角线
U = -triu(A,1); %求 A 的上三角矩阵
w_opt = 2/(1+sqrt(1-(vrho(D(L+U)))^2)); % 最佳松弛因子
if nargin < 4eps = 1e-6;w = w_opt;
end
if nargin < 5w = w_opt;
end
Lw = (D-w*L)((1-w)*D+w*U);
f = w*((D-w*L)b);x_exact = Ab;
it = 1;
for k = 1:I-1x = Lw*x+f;if norm(x-x_exact)>epsit = it+1;end
endt = toc;
end

还是计算前面那个例子，选择精度为

，松弛因子
：
clear
A = [8 -3 2; 4 11 -1; 6 3 12]; b = [20; 33; 36];
I = 1000;
[x,t,it,w] = SOR(A,b,I,1e-6,1.2)

运行结果为

x =3.0000000000000002.0000000000000001.000000000000000t =0.003814113000000it =13w =1.200000000000000

如果采取默认松弛因子(自动选择最佳松弛因子)：

clear
A = [8 -3 2; 4 11 -1; 6 3 12]; b = [20; 33; 36];
I = 1000;
[x,t,it,w] = SOR(A,b,I)

其结果为

x =3.0000000000000002.0000000000000001.000000000000000t =0.009697537000000it =8w =1.034531942537068

此时迭代次数减少为

次，松弛因子也选择为接近
的数，与高斯-塞德尔迭代法效果基本一致。

4. 共轭梯度(CG)法

也称共轭斜量法，它是一种变分方法，对应于求一个二次函数的极值。CG方法是一种求解大型稀疏对称正定方程组十分有效的方法。

其算法描述为：

（1）任取

，计算
，取
。

（2）对

，计算

（3）若

，或
，计算停止，则
。由于
正定，故当
时，
，而
，也即
。

写成MATLAB代码为

function [x,t,it] = CG(A,b)
% 共轭梯度法 CG(conjugate gradient)
% 针对大型稀疏对称正定矩阵方程组
% 输入：
% A: 系数矩阵
% b: 载荷矩阵
% 输出：
% x: 解矩阵
% t: 时间
% it: 迭代次数tic
[n,~] = size(A);
x = zeros(n,1);
r = b - A*x;
p = r;
it = 0;while (sum(r.*r) ~= 0) && (sum(p.*(A*p)) ~= 0)it = it+1;rr = sum(r.*r);alpha = rr/sum(p.*(A*p));x = x + alpha*p;r = r - alpha*A*p;beta = sum(r.*r)/rr;p = r + beta*p;
end
t = toc;
end

用此CG方法求解一个

阶Hilbert矩阵：
clear
n = 6; A = zeros(n,n);
% Hilbert 矩阵
for i = 1:nfor j = 1:nA(i,j) = 1/(i+j-1);end
end
x_star = ones(n,1); b = A*x_star;
[x,t,it] = CG(A,b)

运行结果为：

x =0.9999999999998971.0000000000040020.9999999999680481.0000000000921610.9999999998907641.000000000045352t =0.006673698000000it =350

而如果采用Gauss-Seidel迭代法，精度要求为

，其结果为
x =0.9999999999998711.0000000000043290.9999999999676931.0000000000897200.9999999998961901.000000000042388t =2.914480589000000it =5438741

对比结果可以发现，达到类似精度，G-S迭代法需要迭代

次迭代，是CG方法的近
倍，足以见得在处理大型稀疏正定矩阵时CG方法的优势之明显。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/411707.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！

相关文章

全文服务（Microsoft 搜索）不可用。系统管理员必须启动此服务

全文服务（Microsoft 搜索）不可用。系统管理员必须启动此服务

全文服务(Microsoft 搜索)不可用。系统管理员必须启动此服务。1.打开sql server服务管理器 2.在服务下拉框中选microsoft seardh 3.点启动 4.并选中当启动os时自动启动服务 转载于:https://www.cnblogs.com/Kennytian/archive/2008/05/30/1210418.html
阅读更多...
防火墙架构解析

防火墙架构解析

防火墙本身就是一台为网络而设计的计算机&#xff0c;与通用计算机一样防火墙是由硬件和软件组成&#xff0c;现今防火墙有着多种硬件技术架构&#xff0c;不同的硬件架构有着各自不同的特点。先说明一下什么是处理器体系结构和体系架构。体 系 架 构 &#xff1a;CPU架构是CPU…
阅读更多...
[html] 你有了解HTML5的地理定位吗？怎么使用？

[html] 你有了解HTML5的地理定位吗？怎么使用？

[html] 你有了解HTML5的地理定位吗&#xff1f;怎么使用&#xff1f; var xdocument.getElementById("demo"); function getLocation() { if (navigator.geolocation) { navigator.geolocation.getCurrentPosition(showPosition); } else { x.innerHTML"该浏览…
阅读更多...
apache 修改服务器配置,Apache服务器配置全攻略

apache 修改服务器配置,Apache服务器配置全攻略

在使用子进程处理HTTP请求的Web服务器上&#xff0c;由于要首先生成子进程才能处理客户的请求&#xff0c;因此反应时间就有一点延迟。但是&#xff0c;Apache服务器使用了一个特殊技术来摆脱这个问题&#xff0c;这就是预先生成多个空余的子进程驻留在系统中&#xff0c;一旦有…
阅读更多...
易驾佳智能机器人教练_机器人教练创始人马宏先生受邀到中国人民大学进行经验分享...

易驾佳智能机器人教练_机器人教练创始人马宏先生受邀到中国人民大学进行经验分享...

4月2日&#xff0c;北京易驾佳信息科技有限公司创始人、机器人教练创始人马宏先生受邀前往中国人民大学&#xff0c;与MBA在学学生分享企业经营管理经验。从个人创业发展历程、多年来对驾培行业的洞察及转型升级方向等方面与大家进行了分享、交流。期间&#xff0c;马宏先生跟大…
阅读更多...
[html] 说说你对＜meta＞标签的理解

[html] 说说你对＜meta＞标签的理解

[html] 说说你对标签的理解 设置meta标签 设置页面长串数字不与跳转防止长串数字电话或以邮箱的形式外链出去 ## 设置meta标签 IE适配用于IE浏览器的适配 设置meta标签 移动端IOS用于适配苹果手机&#xff0c;用于全屏显示 设置meta标签 清除页面缓存Cache-Control头域Cache-C…
阅读更多...
实现控件的随意拖动

实现控件的随意拖动

因为客户要求程序要在浏览器上运行&#xff0c;但是这些信息&#xff08;这个程序只在政府某部门内部使用&#xff09;并不需要公开&#xff0c;所以我们选择使用Windows应用程序&#xff0c;并将该程序嵌入到网页中。。。。 就我个人做的这部分简单的说下&#xff0c;我负…
阅读更多...
导出sql文件_（一）SQL基本知识

导出sql文件_（一）SQL基本知识

一 、SQL的特点1.综合统一&#xff1a;SQL集数据定义语言DDL、数据控制语言DCL的功能于一体&#xff0c;语言风格统一&#xff0c;可以独立完成数据库生 命周期中的全部活动(定义关系模式&#xff0c;插入数据&#xff0c;建立数据库&#xff1b;对数据库中的数据进 行查询和更…
阅读更多...
文件下载时，文件名乱码问题

文件下载时，文件名乱码问题

文件下载时&#xff0c;解决不同浏览器文件名乱码问题 public static String encodeFileName(HttpServletRequest request, String pFileName) {String userAgent request.getHeader("USER-AGENT");try {if (userAgent.contains("msie") || userAgent.con…
阅读更多...
[html] 说说你对影子(Shadow)DOM的了解

[html] 说说你对影子(Shadow)DOM的了解

[html] 说说你对影子(Shadow)DOM的了解 web component的API&#xff0c;用来给组件创建子DOM树&#xff0c;就像楼上说的&#xff0c;不受外部style影响&#xff0c;外部通过选择器查询也不会查到里面来。它有两种模式 open和closed&#xff0c;open模式可以获取shadow root&a…
阅读更多...
的引用_左值、右值、左值引用、右值引用

的引用_左值、右值、左值引用、右值引用

【导读】&#xff1a;本文主要详细介绍了左值、右值、左值引用、右值引用以及move、完美转发。左值和右值左值(left-values)&#xff0c;缩写&#xff1a;lvalues右值(right-values)&#xff0c;缩写&#xff1a;rvalues直接上官网查&#xff0c;我一向倡导自己去懂得原理&…
阅读更多...
常用的开始→运行→输入命令集锦

常用的开始→运行→输入命令集锦

gpedit.msc-----组策略sndrec32-------录音机Nslookup-------IP地址侦测器explorer-------打开资源管理器logoff---------注销命令tsshutdn-------60秒倒计时关机命令lusrmgr.msc----本机用户和组services.msc---本地服务设置oobe/msoobe /a----检查XP是否激活notepad--------打…
阅读更多...
小白兔生小白兔-菲波拉契数列问题

小白兔生小白兔-菲波拉契数列问题

有一对小白兔,从出生后第3个月起每个月都生一对小白兔,小白兔长到第三个月后每个月又生一对小白兔,假如小白兔都不死,问每个月的小白兔总数为多少&#xff1f; 这道题是典型的斐波拉切数列问题&#xff0c;其特点就是从第三列开始就等于前两列之和&#xff0c;算法&#xff1a;…
阅读更多...
[html] 解释下你对GBK和UTF-8的理解？并说说页面上产生乱码的可能原因

[html] 解释下你对GBK和UTF-8的理解？并说说页面上产生乱码的可能原因

[html] 解释下你对GBK和UTF-8的理解&#xff1f;并说说页面上产生乱码的可能原因 gbk和utf8的理解我们这里将以最简单最容易理解的方式来描述GBK和UTF8的区别&#xff0c;以及它们分别是什么。GBK编码&#xff1a;是指中国的中文字符&#xff0c;其它它包含了简体中文与繁体中…
阅读更多...
控制反转_Spring：IOC 控制反转

控制反转_Spring：IOC 控制反转

Spring 概述Spring 是什么Spring 是分层的 Java SE/EE 应用 full-stack (全栈式) 轻量级开源框架。全栈式&#xff1a;对各种主流技术和框架都进行了整合&#xff0c;同时对三层架构都提供解决方案。轻量级和重量级的划分主要依据就是看它使用了多少服务&#xff0c;启动时需要…
阅读更多...
TAB选项卡

TAB选项卡

TAB选项卡&#xff1a;下载用Java Script模仿各种作业系统的选项卡&#xff0c;老外就是牛&#xff0c;不仅支援多样式的即时切换&#xff0c;同时也支援每个选项卡是否附带图示的切换选项&#xff0c;选项卡也可以上下切换。 转载于:https://www.cnblogs.com/meetrice/archive…
阅读更多...
巨蟒python全栈开发flask5

巨蟒python全栈开发flask5

1.轮询&&长轮询&&长连接 2.GeventWebsocket 3.Websocket群聊 4.Websocket单聊 5.websocket握手 6.websocket解密 7.websocket加密转载于:https://www.cnblogs.com/studybrother/p/10717550.html
阅读更多...
[html] js放在html的＜body＞和＜head＞有什么区别？

[html] js放在html的＜body＞和＜head＞有什么区别？

[html] js放在html的和有什么区别&#xff1f; 在浏览器解析HTML中的时候&#xff0c;如果在head标签中遇到了script标签并且是同步执行的&#xff0c;那么就会影响文档的加载&#xff0c;如果引入的过多的同步脚本文件 那么加载会变得非常怪异且卡顿&#xff1b;但是放在body…
阅读更多...
最后一封“情书”

最后一封“情书”

本来以为自己是可以按照自己的想法去维系 可是发现自己的矜持对于你是一种恐惧 从退出“水云”的那天我就懂了 真的懂了 我并没想到“关注”变成了“监视”&#xff0c;这是对我的一种侮辱&#xff0c;比任何都&#xff01; 心境不同了&#xff0c;没时间去做毫无意义的监视调查…
阅读更多...
python向dict里添加_Python有条件地向Dict添加键

python向dict里添加_Python有条件地向Dict添加键

我试图从一个标题列表中生成dict&#xff0c;它将数据列“关联”到同一个实验。例如&#xff0c;我想转向&#xff1a;headers ["A_1","A_2","A_3","B_1","B_2","B_3"]进入^{pr2}$我的代码如下&#xff1a;cols …
阅读更多...
最新文章

Copyright @ 2022~2023