高斯混合模型聚类_GMM: Gaussian Mixed Model（高斯混合模型）

0. 简介

GMM和Kmeans一样也属于聚类，其算法训练流程也十分相似，Kmeans可认为是“硬聚类”，GMM是“软聚类”。

给定数据集X，Kmeans算法流程是这样的----- a 初始化：随机初始k个中心（即k个点，记为μ）；b 矫正数据归属：计算X中每个点与k个中心的距离，并将其归为相距最近的那个中心；c 矫正中心：计算每个中心（共k个）所有点的均值，并将其更新为中心值；d 完成整体训练：循环b和c，直到聚类到“足够好”。

GMM算法流程和Kmeans基本一致，区别在于：a 除了初始化k个中心（μ）外，每个中心还对应一个协方差矩阵（Σ）和混合概率（π），其中μ代表高斯分布的中心，Σ代表高斯分布形状，π代表高斯函数值的大小；b 矫正数据归属，GMM中每个数据点并不完全归属某个中心，而是归属每个中心，只是归属的概率不同；c 矫正中心，每个中心矫正更新时考虑数据集X中的所有点，而非某一部分数据点。

以下使用鸢尾花数据集按照a~d的流程解析GMM；导入鸢尾花数据集如下；

from sklearn import datasets
import numpy as npiris = datasets.load_iris()
X = iris.data
N, D = X.shape
display(X.shape, X[:10])
(150, 4)
array([[5.1, 3.5, 1.4, 0.2],[4.9, 3. , 1.4, 0.2],[4.7, 3.2, 1.3, 0.2],[4.6, 3.1, 1.5, 0.2],[5. , 3.6, 1.4, 0.2],[5.4, 3.9, 1.7, 0.4],[4.6, 3.4, 1.4, 0.3],[5. , 3.4, 1.5, 0.2],[4.4, 2.9, 1.4, 0.2],[4.9, 3.1, 1.5, 0.1]])

即鸢尾花数据集是一个150行4列的矩阵。

1. 初始化

定义聚类数量为3类，每一类都初始化一个中心μ、一个协方差矩阵Σ和混合概率π；

mus = X[np.random.choice(X.shape[0], 3, replace=False)]
covs = [np.identity(4) for i in range(3)]
pis = [1/3] * 3

2. 矫正数据归属

普通高斯概率函数（只有一个中心）如下，其中D是数据维度，此处D=4；

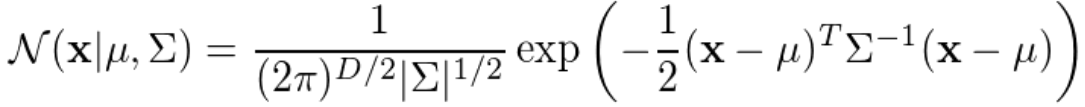
表示数据点x归属该中心（μ、Σ）的概率，代码如下；

def gaussian(X, mu, cov):diff = X - mureturn 1 / ((2 * np.pi) ** (D / 2) * np.linalg.det(cov) ** 0.5) * np.exp(-0.5 * np.dot(np.dot(diff, np.linalg.inv(cov)), diff))

当用混合高斯函数（即多个中心）时，表示一个数据点n归属中心k（μ_k、Σ_k）的概率函数如下，其中k表示第k个中心，此处总共有3个中心，即K=3；

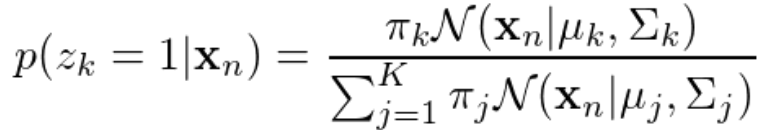
将上式定义为γ_z_nk，即

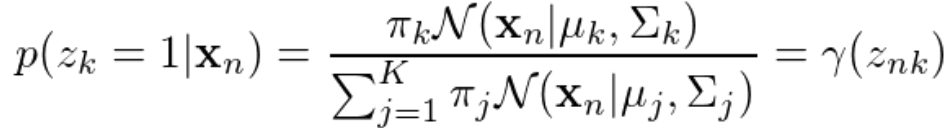
代码如下：

gammas = []
for mu_, cov_, pi_ in zip(mus, covs, pis):# loop each centergamma_ = [[pi_ * gaussian(x_, mu_, cov_)] for x_ in X]# loop each pointgammas.append(gamma_)
gammas = np.array(gammas)
gamma_total = gammas.sum(0)
gammas /= gamma_total

3. 矫正中心

根据2.中的gammas值，更新μ、Σ和π值，公式如下，其中N表示数据总个数，此处N=150；

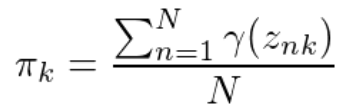
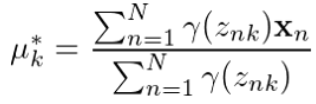
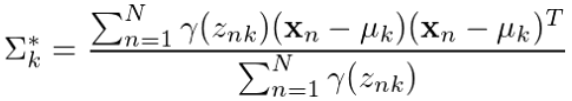
代码如下；

mus, covs, pis = [], [], []
for gamma_ in gammas:#loop each centergamma_sum = gamma_.sum()pi_ = gamma_sum / Nmu_ = (gamma_ * X).sum(0) / gamma_sumcov_ = []for x_, gamma_i in zip(X, gamma_):diff = (x_ - mu_).reshape(-1, 1)cov_.append(gamma_i * np.dot(diff, diff.T))cov_ = np.sum(cov_, axis=0) / gamma_sumpis.append(pi_)mus.append(mu_)covs.append(cov_)

4. 完成整体训练

将2.~3.作为一个循环单元，写成一个函数；

def train_step(X, mus, covs, pis):gammas = []for mu_, cov_, pi_ in zip(mus, covs, pis):# loop each centergamma_ = [[pi_ * gaussian(x_, mu_, cov_)] for x_ in X]# loop each pointgammas.append(gamma_)gammas = np.array(gammas)gamma_total = gammas.sum(0)gammas /= gamma_totalmus, covs, pis = [], [], []for gamma_ in gammas:#loop each centergamma_sum = gamma_.sum()pi_ = gamma_sum / Nmu_ = (gamma_ * X).sum(0) / gamma_sumcov_ = []for x_, gamma_i in zip(X, gamma_):diff = (x_ - mu_).reshape(-1, 1)cov_.append(gamma_i * np.dot(diff, diff.T))cov_ = np.sum(cov_, axis=0) / gamma_sumpis.append(pi_)mus.append(mu_)covs.append(cov_)return mus, covs, pis

训练50次；

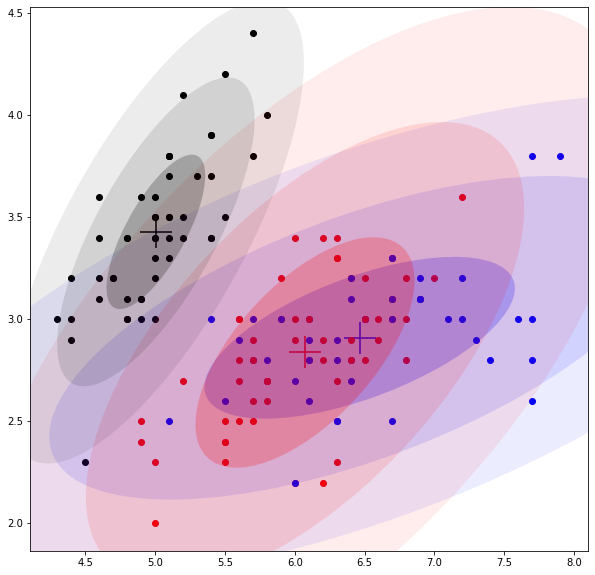
for _ in range(50):mus, covs, pis = train_step(X, mus, covs, pis)

训练完成后，会得到3个中心，可计算每个点归属这三个中心的概率（即γ_z_nk，第n个点归属第k个中心的概率），并将其归属于概率最大的那个中心；因为数据集是4维，无法可视化，仅选择前两维度进行可视化展示如下；

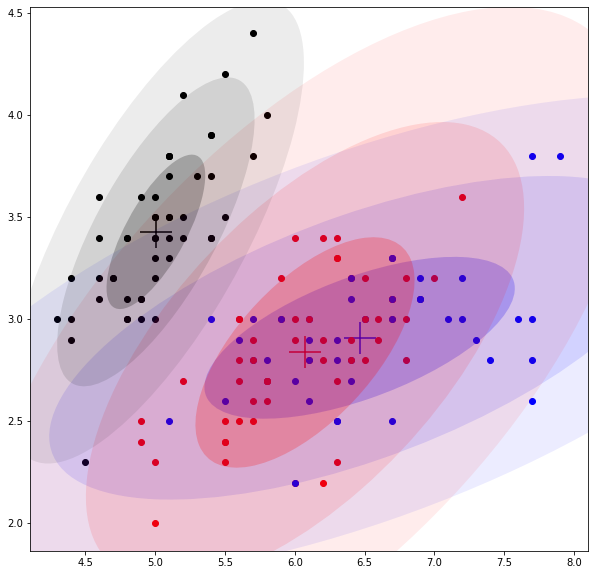
整个训练过程的动态图如下；

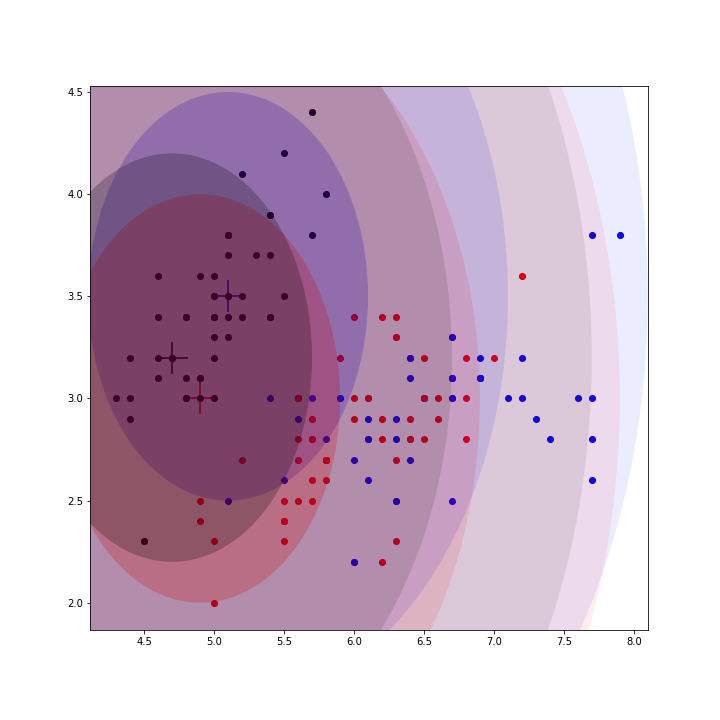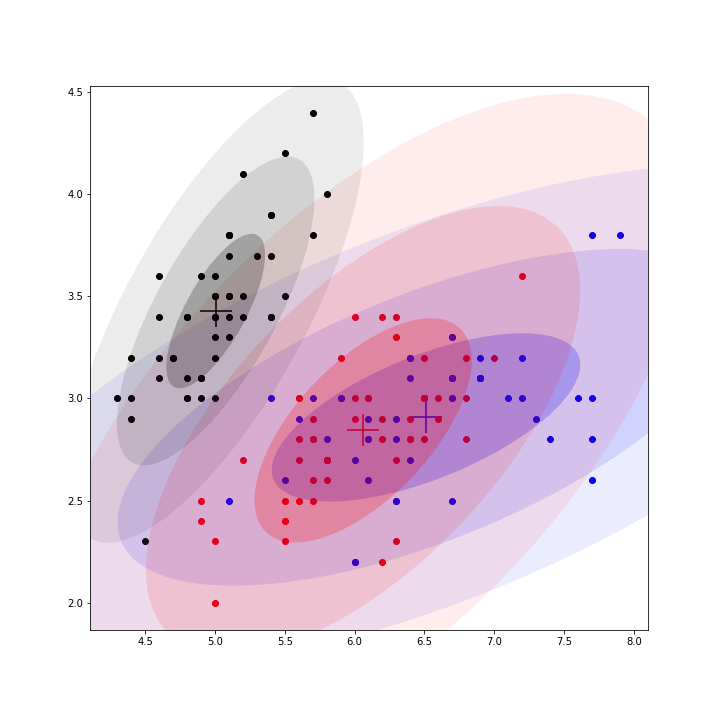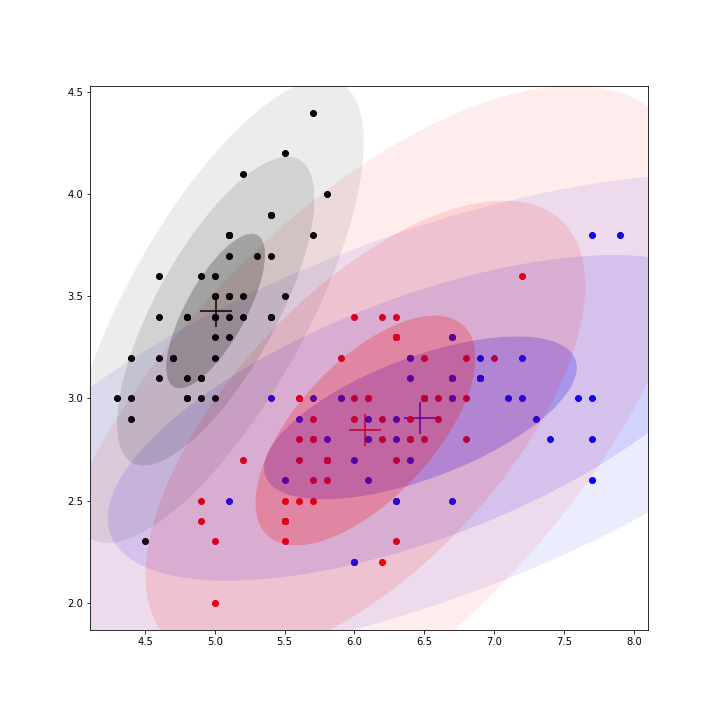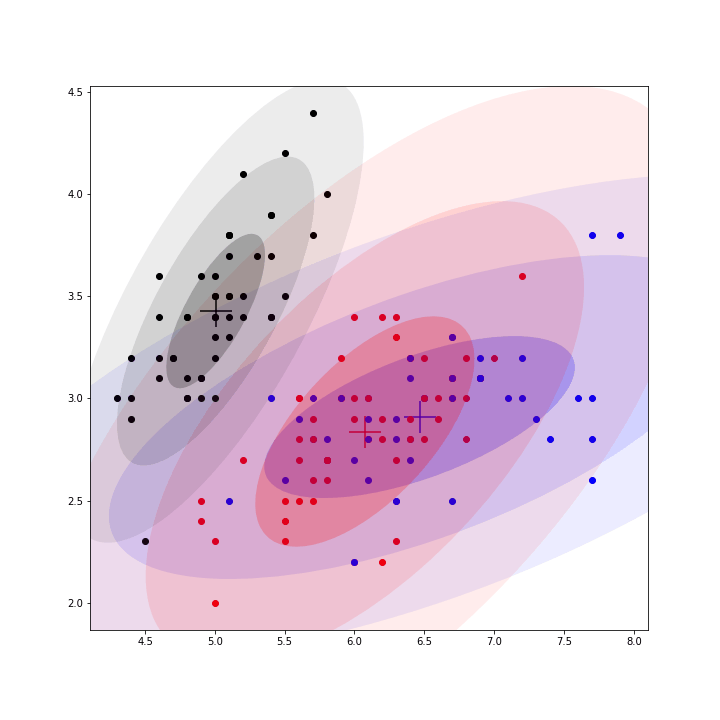
完整代码如下；

from sklearn import datasets
import numpy as np
import matplotlib.pyplot as pltiris = datasets.load_iris()
X = iris.data
N, D = X.shapemus = X[np.random.choice(X.shape[0], 3, replace=False)]
covs = [np.identity(4) for i in range(3)]
pis = [1/3] * 3def gaussian(X, mu, cov):diff = X - mureturn 1 / ((2 * np.pi) ** (D / 2) * np.linalg.det(cov) ** 0.5) * np.exp(-0.5 * np.dot(np.dot(diff, np.linalg.inv(cov)), diff))def get_likelihood(gamma_total):return np.log(gamma_total).sum()def train_step(X, mus, covs, pis):gammas = []for mu_, cov_, pi_ in zip(mus, covs, pis):# loop each centergamma_ = [[pi_ * gaussian(x_, mu_, cov_)] for x_ in X]# loop each pointgammas.append(gamma_)gammas = np.array(gammas)gamma_total = gammas.sum(0)gammas /= gamma_totalmus, covs, pis = [], [], []for gamma_ in gammas:#loop each centergamma_sum = gamma_.sum()pi_ = gamma_sum / Nmu_ = (gamma_ * X).sum(0) / gamma_sumcov_ = []for x_, gamma_i in zip(X, gamma_):diff = (x_ - mu_).reshape(-1, 1)cov_.append(gamma_i * np.dot(diff, diff.T))cov_ = np.sum(cov_, axis=0) / gamma_sumpis.append(pi_)mus.append(mu_)covs.append(cov_)return mus, covs, pis, gamma_totallog_LL = []
for _ in range(50):mus, covs, pis, gamma_total = train_step(X, mus, covs, pis)log_LL.append(get_likelihood(gamma_total))
plt.plot(log_LL)
plt.grid()

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.mzph.cn/news/410481.shtml

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈email:809451989@qq.com，一经查实，立即删除！