继续是机器学习课程的笔记，本节内容主要是介绍大规模机器学习的内容。

大型数据集的学习

对于一个过拟合的模型，增加数据集的规模可以帮助避免过拟合，并获得一个更好的结果。

但是对于一个大规模的数据，比如有100万个数据量的训练集，其计算量是非常大的。以线性回归模型为例，每一次梯度下降迭代，我们都需要计算训练集的误差的平方和，对于训练集有上百万的数据量，如果学习算法需要有20次迭代，这就已经是一个非常大的计算代价。

因此，首先需要确定是否需要有这么大规模的训练集，也许只用1000个训练集就能获得比较好的结果，这一步可以通过绘制学习曲线来帮助判断，如下所示：

随机梯度下降法(Stochastic Gradient Descent)

如果一定需要一个大规模的训练集，我们可以尝试使用随机梯度下降法来代替批量梯度下降法。

批量梯度下降算法在每次迭代的时候需要计算整个训练集的和，其公式如下：

$$\theta_j := \theta_j-\alpha \frac{1}{m}\sum_{i=1}^m (h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$$
如上公式可以知道，如果训练集的数量m非常大，那么计算量就非常大。

而在随机梯度下降法中，我们定义代价函数为一个单一训练实例的代价：

$$cost(\theta,(x^{(i)},y^{(i)}))=\frac{1}{2} (h_\theta(x^{(i)})-y^{(i)})^2 \\ J_{train}(\theta) = \frac{1}{m}\sum_{i=1}^mcost(\theta,(x^{(i)},y^{(i)}))$$

所以随机梯度下降算法是：

1. 首先对训练集随机“洗牌”，即打乱顺序；
2. 然后重复下列步骤：

Repeat(一般迭代1-10次整个训练集，根据训练集大小选择，训练集越大，迭代次数越小){
for i=1:m{
$\theta_j := \theta_j - \alpha(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}$
(for j = 0:n)
}
}

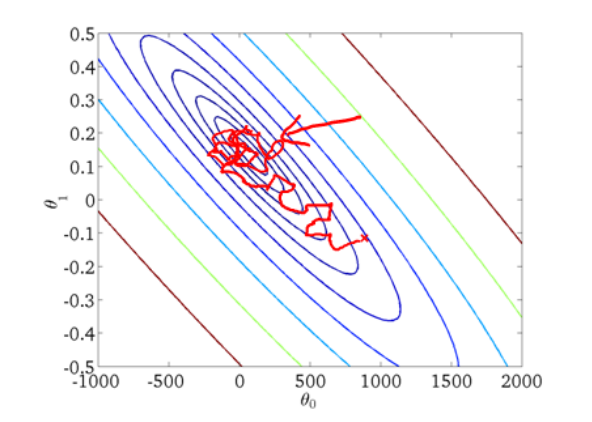
随机梯度下降算法在每一次计算之后便更新参数$\theta$,而不需要首先将所有的训练集求和，在批量梯度下降算法还没有完成一次迭代时，随机梯度下降算法便已经走出了很远。但缺点是，不是每一步都是朝着“正确”的方向迈出的，因此算法虽然会逐步走向全局最小值的位置，但是可能无法站到那个最小值的那一点，而是在最小值点附近徘徊。如下图所示

微型批量梯度下降（Mini-Batch Gradient Descent)

接下来介绍第三种梯度下降算法--微型批量梯度下降算法，它是介于批量梯度下降算法和随机梯度下降算法之间的算法，每次迭代使用b个训练实例，更新一次参数$\theta$，其更新公式如下所示：

Repeat{
for i=1:m{
$\theta_j := \theta_j - \alpha \frac{1}{b} \sum_{k=i}^{i+b-1}(h_\theta(x^{(k)})-y^{(k)})x_j^{(ik}$
(for j = 0:n)
i+=10;
}
}

也就是如果令b=10，m=1000，有：

Repeat{
for i=1,11,21,31,…,991{
$\theta_j := \theta_j - \alpha \frac{1}{10} \sum_{k=i}^{i+9}(h_\theta(x^{(k)})-y^{(k)})x_j^{(ik}$
(for j = 0:n)
}
}

通常会令b在2~100之间。这样做的好处是，我们可以用向量化的方式来循环b个训练实例，如果我们用的线性代数函数库比较好，能够支持平行处理，那么算法的总体表现将不受影响（与随机梯度下降算法相同）。有时甚至可以比随机梯度下降算法更快。

随机梯度下降收敛

接下来介绍随机梯度下降算法的调试，以及学习率$\alpha$的选取。

在批量梯度下降中，我们可以令代价函数J为迭代次数的函数，绘制图表，根据图表来判断梯度下降是否收敛，但是，在大规模的训练集的情况下，这是不现实的，因为计算代价太大了。

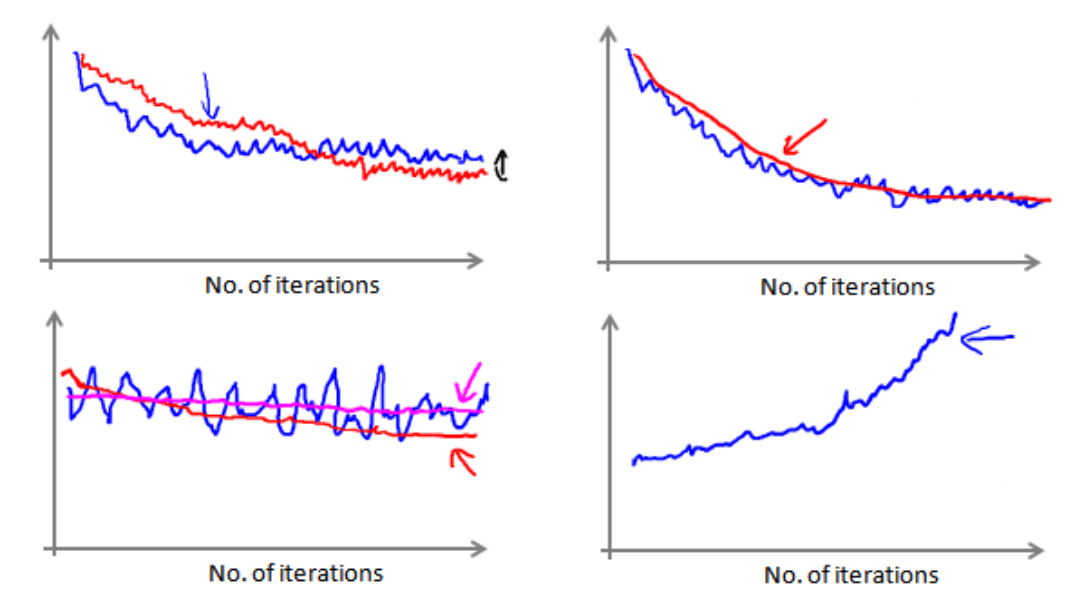
在随机梯度下降算法中，我们在每一次更新$\theta$之前都计算一次代价，然后每X次迭代后，求出这X次对训练实例计算代价的平均值，然后绘制这些平均值与X次迭代的次数之间的函数图片。比如令X=1000,即每1000次迭代就计算一次代价的平均值，然后绘制图表。如下图所示：

当我们绘制这样的图表时，可能会得到一个颠婆不平但是不会明显减少的函数图象（如上图中左下图蓝线所示）。我们可以增加X，如令X=5000,来使得函数更平缓，也许便能看出下降的趋势（如上图中左下图的红线所示）；但可能函数图表仍然是颠婆不平且不下降的（还是左下图的洋红色曲线，即上面那条），这可能就是模型本身存在一些错误。

而如果得到的曲线是如上图中右下图所示，不断地上升，那么可能需要选择一个较小的学习率$\alpha$。

我们可以令学习率随着迭代次数的增加而减少，如下所示：

$$\alpha = \frac{const1}{iterationNumber + const2}$$

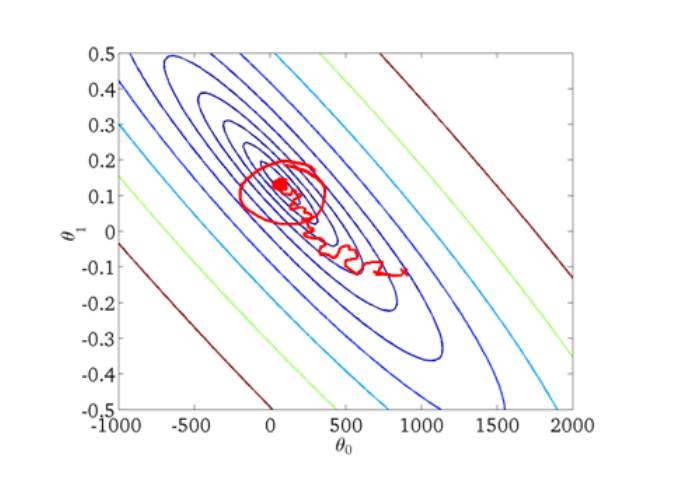
随着不断地靠近全局最小值，通过减小学习率，我们迫使算法收敛而非在最小值附加徘徊，如下图所示。

但是通常我们不需要这样做便能有非常好的效果了，对$\alpha$进行调整所耗费的计算通常不值得，毕竟这种调整学习率方法需要确定常数const1和const2的值。

在线学习

接下来介绍一种新的大规模机器学习机制–在线学习机制。在线学习算法指的是对数据流而非离线的静态数据集的学习。许多在线网站都有持续不断的用户流，对于每一个用户，网站希望能在不将数据存储到数据库中便顺利地进行算法学习。

假设我们正在经营一家物流公司，每当一个用户询问从地点A至地点B的快递费用时，我们给用户一个报价，该用户可能选择接受（y=1）或者不接受（y=0）。

现在，我们希望构建一个模型，来预测用户接受报价使用我们的物流服务的可能性。因此报价是一个特征，其他特征为距离，起始地点，目标地点以及特定的用户数据。而模型的输出是p（y=1）。

在线学习的算法与随机梯度下降算法有些类似，我们对单一的实例进行学习，而非对一个提前定义的训练集进行循环。

Repeat forever (as long as the website is running){
对当前用户获取对应的(x,y)
$\theta_j := \theta_j- \alpha(h_\theta(x) - y)x_j$
(for j= 0:n)
}

一旦对一个数据的学习完成了，我们便可以丢弃该数据，不需要再存储它了。这种方式的好处是，我们的算法可以很好的适应用户的倾向性，算法可以针对用户的当前行为不断地更新模型以适应该用户。

其他在线学习的例子有如搜索，比如搜索拥有1080p像素相机的安卓手机等。

映射化简和数据并行

映射化简和数据并行对于大规模机器学习问题而言是非常重要的概念。

之前提到，如果我们用批量梯度下降算法来求解大规模数据集的最优解，我们需要对整个训练集进行循环，计算偏导数和代价，再求和，计算代价非常大。如果我们能够将我们的数据集分配给多态计算机，让每一台计算机处理数据集的一个子集，然后我们将计算的结果汇总再求和，这样的方法叫做映射简化。

具体而言，如果任何学习算法能够表达为，对训练集的函数的求和，那么便能将这个任务分配给多台计算机（或者同一台计算机的不同CPU），以达到加速处理的目的。

例如，我们有400个训练实例，我们可以将批量梯度下降的求和任务分配给4台计算机进行处理：

很多高级的线性代数函数库已经能够利用多核CPU的多核来平行地处理矩阵运算，这也是算法的向量化实现如此重要的缘故，这比使用循环更快。

小结

本节课内容介绍了如此使用大规模数据集来进行训练机器学习算法，介绍了两种新的梯度下降算法–随机梯度下降和微型批量梯度下降，以及新的大规模机器学习算法机制–在线学习机制，最后介绍了映射化简和数据并行，也就是使用多台计算机或者是同一台计算机的多个CPU分别计算训练集的一个子集，最后再将结果汇总求和的方法。