(1)线段检测应用背景
(2)线段检测原理简介
(3)线段检测实例 a line segment detector
(4)hough 变换和 lsd 的区别
---------------------author:pkf
------------------------------time:2015-1-26
-----------------------------------------qq:1327706646
(1)线段检测应用背景
线段检测在高铁电机机车顶部图像检测系统中有很大应用,像受电弓检测程序之类的,很有必要,最近也是客户有这个需求,做lsd移植发现的。
http://wenku.baidu.com/link?url=Tsm6xLIA1Dx2VQECCpY8xpMRWm0bcnJ0Ivn_dk4Nb5DcEwPVqOE9pn55sBpHvt8aKqe7s6XLMcyHNLMkJbAn-iqO9uPbVbrkApmGSVqOLf3 机车顶部图像检测系统方案!
http://www.baidu.com/s?ie=utf-8&f=8&rsv_bp=1&rsv_idx=1&tn=baidu&wd=受电弓检测程序&rsv_pq=b0f1b87b000047b9&rsv_t=17eaouGpLbNXKYoRVknb%2B3%2BRaEZADB3lfcGpq7nR%2FQCM9hZcVI2x7vj%2FgaE&rsv_enter=1&inputT=1014&rsv_sug3=4&rsv_n=2&rsv_sug2=0&rsv_sug4=1872
(2)线段检测简介
为提高数字图像中的直线的检测速度,从时频域变换和空间域变换两个角度出发,提出了一种改进型数字图像中直线快速检测方法。首先,采用小波提升提取图像中的低频轮廓信息,抑制高频噪声。然后,对像素降低后的图像进行二值化处理;基于"两点确定一条直线"以及Hough变换过程中"图像空间中一条直线上的多个点对应参数空间中一个点"的原理,按照从局部到整体的检测顺序,将二值化后图像空间中的非零点映射到参数空间中具有较大存在概率的累加单元,而不是所有可能的累加单元。最后,对累加单元进行统计,以确定图像中直线的参数。利用该方法对一幅像素为128×128的数字图像进行直线检测,耗时为213 ms。
首先,我们需要回顾一下,为什么需要检测图像中的直线段?直线段作为图像中边缘的一种,又有什么特殊之处呢?在Marr关于视觉的计算理论中提到,视觉是一种处理过程,经过这个过程我们能从图像中发现外部世界中有什么东西和它们在什么地方。同时,我们还知道,信息处理具有三个层次:(1)第一个层次是信息处理的计算理论(theory),也就是研究是对什么信息进行计算和为什么要进行这些计算;(2)第二个层次是算法(algorithm),也就是如何进行所需要的计算,或者说是设计算法;(3)第三个层次是实现算法的机制,也就是研究某一算法的特定构成。对于视觉系统,观看图像的过程,也可以看做是信息处理的过程。从图像推理得到物体的形状信息的过程也可以对应为三个阶段:(1)初始简图(primal sketch),这个初始简图可以是轮廓图像,也可以是一堆具有特定意义的特征点构成的掩码,或者是像素的光强等信息;(2)2.5维简图(2.5 dimensional sketch),2.5维简图是对初始简图进行一系列的处理和运算,推导出的一个能反映某些几何特征的表象,它和初始简图都是以观察者为核心;(3)三维模型(3D model)。
那么哪些信息可以用来构造图像的初始简图呢?一个形象的例子是画画。画家速写时,用很少的边,点,线等符号,就可以勾勒出大致的景物。当然,这样的景物与实际景物在人体视网膜上产生的以像素为单位的亮度矩阵式不一样的,但是人们也可以轻松的识别出他们。这说明视觉对图形所做的第一个运算就是把他们转换成一些原始符号构成的描述,这些描述所反映的不止是亮度的绝对值的大小,还有图像中的亮度变化和局部的几何特征。
初始简图是一种基元。它可以由若干边缘段(edge segments),线(line segment),斑点(blob)和端点(terminations)构成,这些杂乱的基元构成的初始简图又被称作未处理的初始简图,当这些基元通过各种方式进行聚合、概括和抽象以形成更大、更加抽象的标记(tokens)时,这样的初始简图又被称为完全的初始简图。
这也就是边缘检测之所以称为图像处理和机器视觉的基本问题的原因。边缘检测的直接目的是寻找未处理的初始简图。它通常寻找图像中亮度变化明显的点,当这些点位置相邻且方向相近时,则构成了边缘中的特殊边缘-直线段。目前流行的直线检测算法主要是霍夫变换,它的优势是不受图像旋转的影响,易于进行几何图像的快速变换。基于霍夫变换的改进方法也很多,其中一个重要的方法是广义霍夫变换,可以用来检测任意形状的曲线。
最简单的霍夫变换是在图像中识别直线。在平面直角坐标系(x-y)中,一条直线可以用方程
表示。对于直线上一个确定的点( ,
,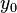 ),有
),有
这表示参数平面(k-b)中的一条直线。因此,图像中的一个点对应参数平面中的一条正弦曲线,图像中的一条直线对应参数平面中的一个点。对图像上所有的点作霍夫变换,最终所要检测的直线对应的一定是参数平面中直线相交最多的那个点。这样就在图像中检测出了直线。在实际应用中,直线通常采用参数方程
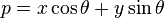 .
.
类似的还有检测线段、圆、圆弧、椭圆、矩形等的霍夫变换。
废话了这么多,终于开始回顾LSD了,使用LSD主要是在遥感图像中几何形状明显的目标进行检测时用到。利用LSD,可以快速的检测图像中的直线段,然后根据目标的几何特征设计快速算法,以快速确定疑似目标区域。
LSD的核心是像素合并于误差控制。利用合并像素来检测直线段并不是什么新鲜的方法,但是合并像素的方法通常运算量较大。LSD号称是能在线性时间(linear-time)内得到亚像素级准确度的直线段检测算法。LSD虽然号称不需人工设置任何参数,但是实际使用时,可以设置采样率和判断俩像素是否合并的方向差。我们知道,检测图像中的直线其实就是寻找图像中梯度变化较大的像素。因此,梯度和图像的level-line是LSD提及的两个基本概念。LSD首先计算每一个像素与level-line的夹角以构成一个level-line场。然后,合并这个场里方向近似相同的像素,这样可以得到一系列regions,这些 regions被称为 line support regions。如下图所示。
每一个line support region其实就是一组像素,它也是直线段(line segment)的候选。同时,对于这个line support region,我们可以观察它的最小外接矩形。直观上来讲,当一组像素构成的区域,特别细长时,那么这组像素更加可能是直线段。基于此,作者还统计了line support region的最小外接矩形的主方向。line support region中的一个像素的level-line 角度与最小外接矩形的主方向的角度差在容忍度(tolerance)2τ内的话,那么这个点被称作"aligned point"。作者统计最小外接矩形内的所有像素数和其内的alinedg points数,用来判定这个line support region是否是一个直线段。判定的准则使用的是“a contrario approach”和“Helmholtz principle”方法。在这里,aligned points的数量是我们感兴趣的信息。因此作者考虑如下假设:aligned points越多,那么region越可能是直线段。对于一副图像i和一个矩形r,记k(i,r)为aligned points的数量,n(r)为矩形r内的总像素数。那么,我们希望能够看到:
其中,Ntest是所有要考虑的矩形的数量。PH0是针对 contrario model H0的一个概率。I是在H0模型下的随机图像。在这篇文章中,作者用H0的模型,主要有以下两个属性:
(1){LLA(j)},其中j是像素,是一由一组随机变量组成;(2)LLA(j)在[0,2π]上均匀分布。
因此,判断一个像素是不是aligned point可以记作概率:
p = τ/π
这样,再通过误差控制,最终的直线段检测算法如下:
在上述算法中,还有两个要点我们没有解释。一是line support region具体是怎么得到了,二是怎样进行误差控制的。
前面我们说过,line support region是通过合并方向近似相同的像素得到。其实在这里,这个合并的过程更多的是依赖于区域生长算法。对于一个level-line 场LLA,种子像素P,和容忍度 τ。我们 可以通过简单的区域生长算法来得到line support region,具体的算法过程参考论文里给出的步骤吧。
至于NFA(the number of false alarms)计算,作者使用如下公式计算:
其中,N和M是采样过后图像的列和行,B(n,k,p)是一个二项分布。n依旧是矩形内所有像素数,k是矩形内的所有p-aligned point数。此处的p-aligned point是指和矩形的主方向在容忍度pπ下方向相同的像素。如果
在实际使用作者的源码时,可以调整lsd函数中的scale来调整图像采样率。此外,合并角度代码里默认是22.5度。图像越小,角度越小,得到的结果越少。不过当图像采样不同时,在同一位置可能得到差异特别大的直线段,这个暂时不知道是什么造成的。
一个比较迷人的结果:
http://blog.csdn.net/polly_yang/article/details/10085401
http://blog.csdn.net/carson2005/article/details/9326847
http://coursegraph.com/category/math
http://blog.csdn.net/polly_yang/article/category/1243538 pgm 公开课
(3)线段检测实例 a line segment detector
有带缩放的高斯下采样,也有1.0的不缩放的检测
http://www.ipol.im/pub/art/2012/gjmr-lsd/?utm_source=doi v1.6
http://blog.csdn.net/tianwaifeimao/article/details/17678669
(4)hough 变换和 lsd 的区别
http://blog.csdn.net/tianwaifeimao/article/details/17678669 各自优缺点
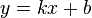











)



-代码生成)










