A standard deviation seems like a simple enough concept. It’s a measure of dispersion of data, and is the root of the summed differences between the mean and its data points, divided by the number of data points…minus one to correct for bias.

标准偏差似乎很简单。 它是对数据分散性的一种度量，是均值与其数据点之和的总和之差除以数据点的数量…… 减去1即可校正偏差 。

This is, I believe, the most oversimplified and maddening concept for any learner, and the intent of this post is to provide a clear and intuitive explanation for Bessel’s Correction, or n-1.

我认为，对于任何学习者来说，这都是最简单和令人发疯的概念，这篇文章的目的是为贝塞尔修正(n-1)提供清晰直观的解释。

To start, recall the formula for a population mean:

首先，回顾一下总体均值的公式：

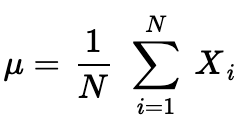
What about a sample mean?

样本的意思是什么？

Well, they look identical, except for the lowercase N. In each case, you just add each xᵢ, and divide by how many x’s there are. If we are dealing with an entire population, we would use N, instead of n, to indicate the total number of points in the population.

好吧，除了小写字母N之外，它们看起来相同。在每种情况下，您只需将每个xᵢ相加，然后除以x的个数即可。 如果要处理整个总体，则将使用N而不是n来表示总体中的总点数。

Now, what is standard deviation σ (called sigma)?

现在，标准偏差σ是多少？

If a population contains N points, then the standard deviation is the square root of the variance, which is the summed-and-averaged squared differences of each data point and the population mean, or μ:

如果总体包含N个点，则标准偏差为方差的平方根，即每个数据点与总体平均值或μ的求和平均值平方差。

But what about a sample standard deviation, s, with n data points and sample mean x-bar:

但是，具有n个数据点和样本均值x-bar的样本标准偏差s呢？

Alas, the dreaded n-1 appears. Why? Shouldn’t it be the same formula? It was virtually the same formula for population mean and sample mean!

,，出现了可怕的n-1。 为什么？ 不应该是相同的公式吗？ 总体均值和样本均值实际上是相同的公式！

The short answer is: this is very complex, to such an extent that most instructors explain n-1 by saying the sample standard deviation will ‘a biased estimator’ if you don’t do it.

简短的答案是： 这非常复杂，以至于大多数教师讲n-1时，如果不这样做，则样本标准差将成为“有偏估计”。

什么是偏见，为什么存在？ (What is Bias, and Why is it There?)

The Wikipedia explanation can be found here.

Wikipedia的解释可以在这里找到 。

It’s not helpful.

没有帮助

To really understand n-1, just like any other brief attempt to explain Bessel’s Correction, requires holding a lot in your head at once. I’m not talking about a proof, either. I’m talking about truly understanding the differences between a sample and a population.

要真正了解N-1，就像任何其他的简短试图解释贝塞尔修正，需要立刻拿着很多在你的头上。 我也不是在说证明。 我说的是真正了解样本与总体之间的差异 。

What is a sample?

什么是样本？

A sample is always a subset of a population it’s intended to represent (a subset can be the same size as the original set, in the unusual case of sampling an entire population without replacement). This is a massive leap alone. Once a sample is taken, there are presumed, hypothetical parameters and distributions built into that sample-representation.

样品始终是一个人口它意在表示 (一个子集可以是相同大小的原始集合，在没有更换采样的整个人口的不寻常的情况下)的子集 。 单单这是一次巨大的飞跃。 抽取样本后， 该样本表示中会内置假定的假设参数和分布 。

The very word statistic refers to some piece of information about a sample (such as a mean, or median) which corresponds to some piece of analogous information about the population (again, such as mean, or median) called a parameter. The field of ‘Statistics’ is named as such, instead of ‘Parametrics’, to convey this attitude of inference from smaller to larger, and this leap, again, has many assumptions built into it. For example, if prior assumptions about a sample’s population are actually quantified, this leads to Bayesian statistics. If not, this leads to frequentism, both outside the scope of this post, but nevertheless important angles to consider in the context of Bessel’s correction. (in fact, in Bayesian inference Bessel’s Correction is not used, since prior probabilities about population parameters are intended to handle bias in a different way, upfront. Variance and standard deviation are calculated with plain old n).

统计数据一词是指有关样本的某些信息(例如平均值或中位数)，它对应于有关总体的某些类似信息(同样是平均值或中位数)，称为参数。 “统计”字段的名称被这样命名，而不是“参数”字段，以传达从小到大的这种推理态度，而这一飞跃又有许多假设。 例如，如果实际量化了关于样本总体的先前假设，那么这将导致贝叶斯统计 。 如果不是这样，则会导致频频主义 ，这既不在本文讨论的范围之内，也不过是在贝塞尔修正案中要考虑的重要角度。 (实际上，在贝叶斯推断中未使用Bessel校正，因为有关总体参数的先验概率旨在以不同的方式预先处理偏差。方差和标准差使用普通old n来计算)。

But let’s not lose focus. Now that we’ve stated the important fundamental difference between a sample and a population, let’s consider the implications of sampling. I will be using the Normal distribution for the following examples for the sake of simplicity, as well as this Jupyter notebook which contains one-million simulated, Normally distributed data points for visualizing intuitions about samples. I highly recommend playing with it yourself, or simply using from sklearn.datasets import make_gaussian_quantiles to get a hands-on feel for what’s really going on with sampling.

但是，我们不要失去重点。 现在，我们已经说明了样本和总体之间的重要根本区别，让我们考虑一下样本的含义。 为简单起见，我将在以下示例中使用正态分布，以及此Jupyter笔记本 ，其中包含一百万个模拟的正态分布数据点，用于可视化有关样本的直觉。 我强烈建议您自己玩，或者只是from sklearn.datasets import make_gaussian_quantiles来获得对采样实际操作的亲身体验。

Here is an image of one million randomly-generated, Normally distributed points. We will call it our population:

这是一百万个随机生成的正态分布点的图像。 我们称其为人口：

To further simplify things, we will only be considering mean, variance, standard deviation, etc., based on the x-values. (That is, I could have used a mere number line for these visualizations, but having the y-axis more effectively displays the distribution across the x axis).

为了进一步简化，我们将仅基于x值考虑均值，方差，标准差等。 (也就是说，我本可以仅使用数字线进行这些可视化，但是使y轴更有效地显示x轴上的分布)。

This is a population, so N = 1,000,000. It’s Normally distributed, so the mean is 0.0, and the standard deviation is 1.0.

这是人口，因此N = 1,000,000。 它是正态分布的，因此平均值为0.0，标准偏差为1.0。

I took two random samples, the first only 10 points and the second 100 points:

我随机抽取了两个样本，前一个仅10分，第二个100分：

Now, let’s take a look at these two samples, without and with Bessel’s Correction, along with their standard deviations (biased and unbiased, respectively). The first sample is only 10 points, and the second sample is 100 points.

现在，让我们看一下这两个样本(不带贝塞尔校正和不带贝塞尔校正)以及它们的标准偏差(分别为有偏和无偏)。 第一个样本仅为10分，第二个样本为100分。

Take a good long look at the above image. Bessel’s Correction does seem to be helping. It makes sense: very often the sample standard deviation will be lower than the population standard deviation, especially if the sample is small, because unrepresentative points (‘biased’ points, i.e. farther from the mean) will have more of an impact on the calculation of variance. Because the difference between each data point and the sample mean is being squared, the range of possible differences will be smaller than the real range if the population mean was used. Furthermore, taking a square root is a concave function, and therefore introduces ‘downward bias’ in estimations.

请仔细看一下上面的图片。 贝塞尔的矫正似乎确实有所帮助。 这是有道理的：样本标准偏差通常会低于总体标准偏差，尤其是在样本较小的情况下，因为不具有代表性的点(“有偏点”，即距离均值较远)会对计算产生更大的影响差异。 由于每个数据点和样本均值之间的差异均被平方，因此，如果使用总体均值，则可能的差异范围将小于实际范围。 此外， 取平方根是一个凹函数，因此在估计中引入了“向下偏差” 。

Another way of thinking about it is this: the larger your sample, the more of an opportunity you have to run into more population-representative points, i.e. points that are close to the mean. Therefore, you have less of a chance of getting a sample mean which results in differences which are too small, leading to a too-small variance, and you’re left with an undershot standard deviation.

另一种思考方式是：样本越大， 就越有机会碰到更多具有人口代表性的点，即接近均值的点。 因此，您获得样本均值的机会较小，样本均值导致的差异过小，导致方差过小，并且留下的标准偏差不足。

On average, samples of a Normally-distributed population will produce a variance which is biased downward by a factor of n-1 on average. (Incidentally, I believe the distribution of sample biases themselves are described by Student’s t-distribution, determined by n). Therefore, by dividing the square-rooted variance by n-1, we make the denominator smaller, thereby making the result larger and leading to a so-called ‘unbiased’ estimate.

平均而言，正态分布总体的样本将产生方差，该方差平均向下降低n-1倍 。 (顺便说一句，我相信样本偏差本身的分布由Student的t分布描述，由n确定)。 因此，通过将平方根方差除以n-1，我们使分母变小，从而使结果变大，从而导致所谓的“无偏”估计。

The key point to emphasize here is that Bessel’s Correction, or dividing by n-1, doesn’t always actually help! Because the potential sample-variances are themselves t-distributed, you will unwittingly run into cases where n-1 will overshoot the real population standard deviation. It just so happens that n-1 is the best tool we have to correct for bias most of the time.

这里要强调的关键是，贝塞尔校正或除以n-1并不一定总是有帮助！ 因为潜在的样本方差本身是t分布的，所以您会无意中遇到n-1会超出实际总体标准差的情况。 碰巧的是，n-1是大多数时候我们必须校正偏差的最佳工具 。

To prove this, check out the same Jupyter notebook where I’ve merely changed the random seed until I found some samples whose standard deviation was already close to the population standard deviation, and where n-1 added more bias:

为了证明这一点，请查看我只更改了随机种子的同一本Jupyter笔记本 直到我发现一些标准偏差已经接近总体标准偏差的样本，并且其中n-1 增加了更多偏差 ：

In this case, Bessel’s Correction actually hurt us!

在这种情况下，贝塞尔的更正实际上伤害了我们！

Thus, Bessel’s Correction is not always a correction. It’s called such because most of the time, when sampling, we don’t know the population parameters. We don’t know the real mean or variance or standard deviation. Thus, we are relying on the fact that because we know the rate of bad luck (undershooting, or downward bias), we can counteract bad luck by the inverse of that rate: n-1.

因此，贝塞尔的校正并不总是校正。 之所以这样称呼，是因为在大多数情况下，抽样时我们不知道总体参数 。 我们不知道真实的均值或方差或标准差。 因此，我们依靠这样一个事实， 因为我们知道厄运率(下冲或向下偏差)，因此可以通过该比率的倒数来抵消厄运：n-1。

But what if you get lucky? Just like in the cells above, this can happen sometimes. Your sample can occasionally produce the correct standard deviation, or even overshoot it, in which case n-1 ironically adds bias.

但是，如果您幸运的话，该怎么办？ 就像上面的单元格一样，有时可能会发生这种情况。 您的样品有时可能会产生正确的标准偏差，甚至会产生超标，在这种情况下，n-1具有讽刺意味的是会增加偏差。

Nevertheless, it’s the best tool we have for bias correction in a state of ignorance. The need for bias correction doesn’t exist from a God’s-eye point of view, where the parameters are known.

但是，它是我们在无知状态下进行偏差校正的最佳工具。 从参数已知的角度来看，不存在偏差校正的需要。

At the end of the day, this fundamentally comes down to understanding the crucial difference between a sample and a population, as well as why Bayesian Inference is such a different approach to classical problems, where guesses about the parameters are made upfront via prior probabilities, thus removing the need for Bessel’s Correction.

归根结底，这从根本上归结为理解样本与总体之间的关键差异，以及为什么贝叶斯推理是对古典问题的如此不同的方法，其中对参数的猜测是通过先验概率预先做出的 ，从而消除了贝塞尔校正的需要。

I’ll focus on Bayesian statistics in future posts. Thanks for reading!

在以后的文章中，我将重点介绍贝叶斯统计。 谢谢阅读！