576. 出界的路径数

给你一个大小为 m x n 的网格和一个球。球的起始坐标为 [startRow, startColumn] 。你可以将球移到在四个方向上相邻的单元格内（可以穿过网格边界到达网格之外）。你最多可以移动 maxMove 次球。

给你五个整数 m、n、maxMove、startRow 以及 startColumn ，找出并返回可以将球移出边界的路径数量。因为答案可能非常大，返回对 109 + 7 取余后的结果。

示例 1：

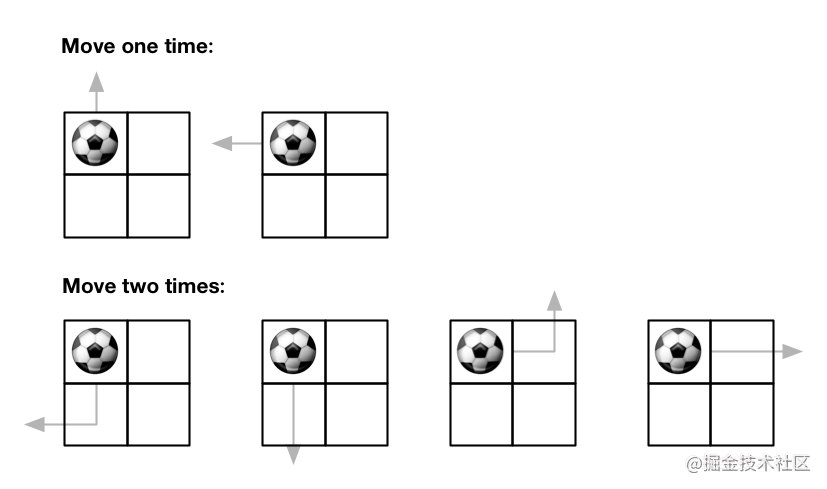
输入：m = 2, n = 2, maxMove = 2, startRow = 0, startColumn = 0
输出：6

示例 2：

输入：m = 1, n = 3, maxMove = 3, startRow = 0, startColumn = 1
输出：12

提示：

1 <= m, n <= 50
0 <= maxMove <= 50
0 <= startRow < m
0 <= startColumn < n

解题思路

数组定义

数组定义dp[i][j]为到达[i][j]时可能的路径数量，因为每一步dp[i][j]的路径数量只和上一步有关，因此我们可以用滚动数组的方法来迭代

状态转移

每个格子可以向其他四个方向移动，所以需要将当前位置的路径数量累加到周围的4个格子，如果移出了边界，则累加进入数组

初始化

球的起始坐标为 [startRow, startColumn] 路径数量置为1

代码

class Solution {public int findPaths(int m, int n, int maxMove, int startRow, int startColumn) {int[][] dir = {{1, 0}, {0, 1}, {-1, 0}, {0, -1}};int[][] dp = new int[m][n];int res=0,mod=1000000007;dp[startRow][startColumn]=1;for (int i=0;i<maxMove;i++){int[][] newDp = new int[m][n];for (int k=0;k<m;k++)for (int j=0;j<n;j++){int old=dp[k][j];if (old>0){for (int[] d : dir) {int r=d[0]+k,c=d[1]+j;if (r>=0&&r<m&&c>=0&&c<n){newDp[r][c]=(old+newDp[r][c])%mod;}else{res=(res+old)%mod;}}}}dp=newDp;}return res;}
}