摘要 (Summary)

In this article, you will learn a little bit about probability calculations in R Studio. As it is a Statistical language, R comes with many tests already built in it, with functions that can save you a lot of work if you know how to use them.

在本文中，您将学到一些有关R Studio中概率计算的知识。 由于R是一种统计语言，因此R内置了许多测试，并且如果您知道如何使用它们，这些函数可以节省大量工作。

We will talk about three of them here:

我们将在这里讨论其中三个：

• Probability for Binomial Distributions
  二项分布的概率
• Probability for Poisson Distributions
  泊松分布的概率
• Probability for Normal Distributions
  正态分布的概率

在我开始之前... (Before I start…)

Alright, you saw the summary, you are interested in this topic but you still didn’t get what does the Ice Cream have to do with all of it, right?

好了，您看到了摘要，您对该主题感兴趣，但是您仍然没有意识到Ice Cream与这一切有什么关系，对吗？

Well, I just wanted to work on this article with an Ice Cream dataset. That’s all. Here is how you can create a small sample in R Studio:

好吧，我只是想使用Ice Cream数据集来撰写本文。 就这样。 这是在R Studio中创建小样本的方法：

ice_cream <- data.frame(month= c(1,2,3,4,5,6,7,8,9,10,11,12),
                        sales= sample(100:500,
                                      size=12, replace=T, 
                                      set.seed(12)),
                        customers= sample(50:450,
                                          size=12, replace=T, 
                                          set.seed(12)))| month| sales| customers|
|-----:|-----:|---------:|
|     1|   127|        77|
|     2|   427|       377|
|     3|   477|       427|
|     4|   208|       158|
|     5|   167|       117|
|     6|   113|        63|
|     7|   171|       121|
|     8|   357|       307|
|     9|   109|        59|
|    10|   103|        53|
|    11|   257|       207|
|    12|   426|       376|

All set. Let’s go!

可以了，好了。 我们走吧！

二项分布 (Binomial Distributions)

Binomial distributions, like the name already tells us, are those where we can get two possible results: Yes/ No, Correct/Wrong, True/False, Success/ Failure.

就像名字已经告诉我们的那样，二项分布是可以得到两个可能结果的分布：是/否，正确/错误，正确/错误，成功/失败。

This test becomes helpful when you need to know the probability of an event to occur if you try it 'n' times.

如果您需要尝试n次尝试知道事件发生的可能性，此测试将很有帮助。

Using our ice cream example, imagine our store has 15 preset cups in the menu, but we wanted to focus on selling Sundae. If we wanted to know what is the probability of a person to come in and choose a Sundae over all the other 15 options, that would fall on a classic problem of statistics: the chance is 1/15 (6.67%), right?

以我们的冰淇淋示例为例，假设我们的商店的菜单中有15个预设杯子，但是我们想专注于销售圣代冰淇淋。 如果我们想知道一个人进入所有其他15个选项中选择圣代的可能性是什么，那将是一个经典的统计问题：几率是1/15(6.67％)，对吗？

But knowing we have more than one customer each day, what would be the probability that 5 customers would choose a Sundae out of every 30 sales transactions? Well, now our problem could be a little bit more complicated to calculate, but it is not, as far as we use the Binomial test in R Studio.

但是，如果知道我们每天有一个以上的客户，那么每30笔销售交易中就有5个客户选择圣代冰淇淋的概率是多少？ 好吧，现在我们的问题可能要稍微复杂一些才能计算出来，但是就我们在R Studio中使用二项式检验而言，并不是这样。

The Binomial test is really simple to perform. You can use the function as follows, where the first parameter will be the number of successes you are measuring(x); the size here is the number of times the event will happen, the number of tries (it should not be confused with the sample size); and the probability of success you have.

二项式检验非常容易执行。 您可以按以下方式使用该函数，其中第一个参数是您正在测量的成功次数( x )； 这里的大小是事件发生的次数，尝试的次数(不应与样本大小混淆)； 以及您成功的可能性 。

dbinom(x= number of successes,
       size = number of events/ tries,
       prob = probability of success)

So, summarizing:

因此，总结一下：

• Problem 1: What is the probability of 5 out of 30 clients to choose Sundae from the menu?

  问题 1：30个客户中有5个从菜单中选择圣代的概率是多少？

• Method: Binomial test = Choose Sundae or NOT Sundae.

  方法 ：二项式检验=选择圣代或不圣代。

• Probability of success: choose 1 over 15 menu options.

  成功的可能性 ：从15个菜单选项中选择1个。

• Number of events: 30 customers = 30 sales transactions.

  事件数 ：30个客户= 30个销售交易。

• Success test: 5 people choose sundae from the menu.

  成功测试 ：5人从菜单中选择圣代冰淇淋。

dbinom(x= 5, size= 30, prob= 1/15)[1] 0.03  # 3% of chance.

And there is more. If we wanted to test the accumulated probability of 5 or more people to choose a Sundae (5, 6, 7, ….30), there is a function for that too. We can use pbinom, which is pretty similar to dbinom, but it brings us the parameter lower.tail, used as TRUE when you want to check a given number of successes or less (q inclusive) and as FALSE when you want more than a given numbers of successes (q exclusive).

还有更多。 如果我们想测试选择一个圣代(5，6，7，….30)的5个或更多人的累积概率，那么也有一个函数。 我们可以使用pbinom ，它与dbinom非常相似，但是它为我们带来了参数lower.tail ，当您要检查给定的成功次数或更少次数(包括q在内)时，此参数为TRUE；而当您希望大于a时，此参数为FALSE给定成功次数( q排除)。

# Information: 5 people or more, 30 sales, prob 1/15
pbinom(q=4, size= 30, prob= 1/15, lower.tail= F)[1] 0.0464 # 4.6% of chance.

Side note: I know you’re probably thinking now "But a choice of a product by a customer is much more complex than a simple statistic test". And indeed, it is. It involves pricing, promotion, value, the store and many other things. But the idea in this article is just to show you how to perform the tests and have it as a new tool for your analysis.

旁注： 我知道您现在可能正在思考“但是，客户选择产品要比简单的统计测试复杂得多”。 确实如此。 它涉及定价，促销，价值，商店和许多其他方面。 但是本文的想法只是向您展示如何执行测试并将其作为分析的新工具。

泊松分布 (Poisson Distributions)

The Poisson Distribution (discovered by Siméon Denis Poisson) is related to events in a period of time.

泊松分布(由SiméonDenis Poisson发现)与一段时间内的事件有关。

You use the Poisson distribution when you want to know what is the chance of something happen 'n' times during a period of time.

当您想知道某一段时间内某事物发生“ n”次的可能性是什么时，您可以使用泊松分布。

In order to use that test, you can type dpois in R Studio. However, you will need to have the following information to proceed:

为了使用该测试，您可以在R Studio中键入dpois 。 但是，您将需要具备以下信息才能继续：

dpois(x= number to test,
      lambda = average rate the event occurs)

Once again, bringing it to our sweet ice cream example, in the dataset presented in the beginning of this article, we see the columns month, sales and customers. So we know our time period is one month. And if we run a summary in our sales column, we will have the average rate for sales by one month, correct?

再次将其带到我们的甜冰淇淋示例中，在本文开头提供的数据集中，我们可以看到月份，销售额和客户列。 所以我们知道我们的时间是一个月。 而且，如果我们在“销售”列中进行汇总，那么我们将有一个月的平均销售率，对吗？

summary(ice_cream$sales)  Min.   1st Qu.  Median  Mean    3rd Qu.    Max. 
  103.0   123.5   189.5   245.2   374.2     477.0

Our lambda is, therefore, 245.2 sales per month. Now we just need to know what we want to test.

因此，我们的lambda是每月245.2销售。 现在，我们只需要知道我们要测试的内容即可。

I want to increase 5% my sales average. How probable is that to happen, just by chance?

我希望将平均销售收入提高5％。 偶然发生的可能性有多大？

• Problem 2: Increase the average sales/month in 5%, to approx. 257?

  问题2 ：将每月平均销售额提高5％，达到 257？

• Method: Poisson test = 12 more sales per month

  方法 ：泊松测试=每月增加12次销售

• Current average: 245.2 (lambda)

  目前平均 ：245.2(lambda)

dpois(x= 257, lambda= 245.2)[1] 0.0188  # 1.8% of chance

Yeah. I better start working more on marketing actions, right? Because if I leave it to chance, I will have to rely on tiny 1.8% of probability that the customers will start to appear in my store and buy more.

是的 我最好开始更多地从事营销活动，对吗？ 因为如果我把它留给机会，我将不得不依靠很小的1.8％的可能性使客户开始出现在我的商店中并购买更多商品。

Similarly to the other distribution tests, the Poisson also brings the ppois that calculates the accumulated probability. The difference is only the function name starting with the letter p and the inclusion of the lower.tail parameter.

与其他分布测试类似，泊松也带来了ppois来计算累积概率。 区别只是函数名称以字母p开头，并包含lower.tail参数。

Now I will calculate the cumulative chance of increasing my sales anywhere between 1% and 5%.

现在，我将计算在1％到5％之间的任意位置增加销售量的累积机会。

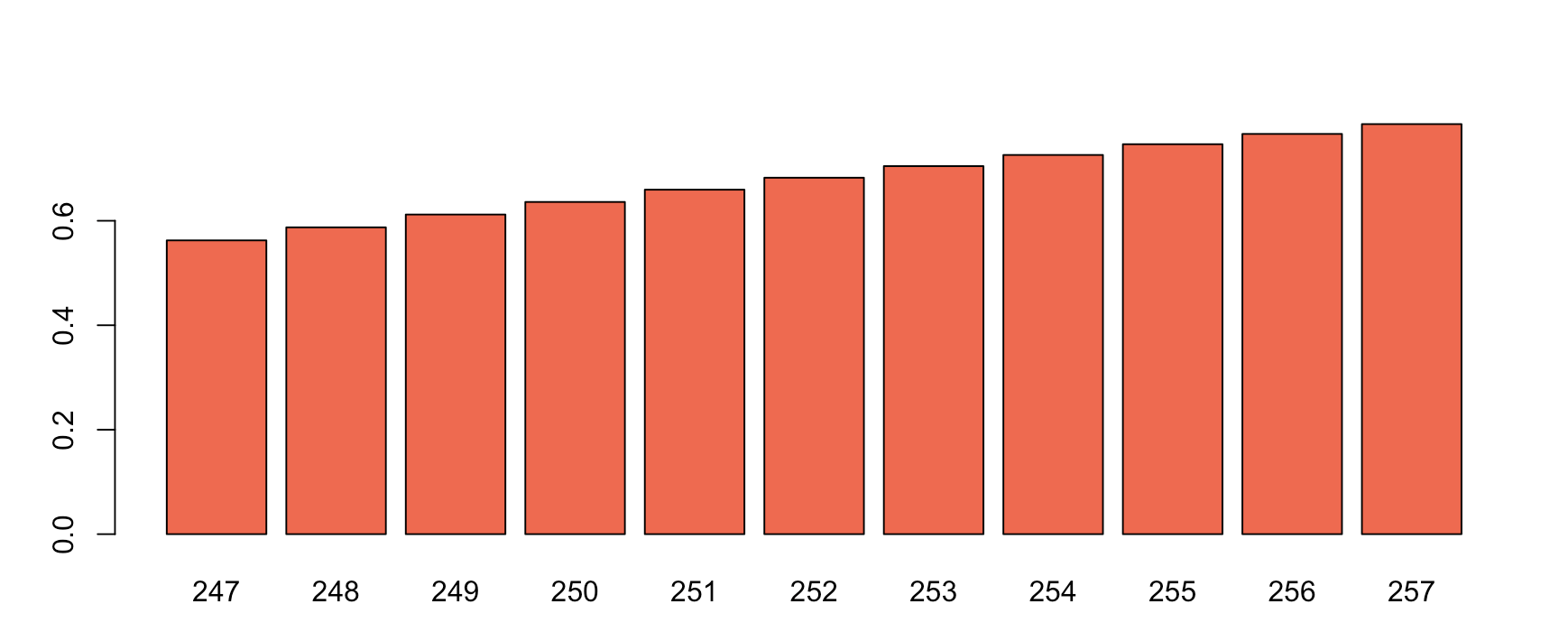
# Calculating the accumulated prob. of 5% increase or less and subtracting the prob. of 1% or less. This way I get only the exact interval between 1% and 5%, nothing over or below it.ppois(257, lambda = 245.2) - ppois(247, lambda = 245.2)[1] 0.2226  # 22% of chance!

Remember, this is the addition of the chances. So, increasing 5% holds the sum of the chances to increase 1%+2%+3%+4%+5% or any decimals between. That way, you must be really careful when plotting and reading a graphic like the one below. It shows 56% of chance to increase 1% of our sales. Come on! What does it mean?

记住，这是机会的增加。 因此，增加5％就是增加1％+ 2％+ 3％+ 4％+ 5％或两者之间任何小数的机会之和。 这样，在绘制和读取下面的图形时，您必须非常小心。 它显示出56％的机会增加了我们1％的销售额。 来吧！ 这是什么意思？

Where the picture shows 247 (or approx. 1% increase), we are actually calculating the accumulated probability of the sales go from the average of 245.2 to any number until 247 — anywhere from 0 to 1%. Even a minor change of 0.01, like 245.2 to 245.21 is considered and added to the probability calculation in this case. Thus, looking at the first bar in the graphic, it is not correct to say that you will be seated all day and it is 56% probable that your sales will go up by 1%.

当图片显示为247(或增长约1％)时，我们实际上是在计算销售的累计概率，从平均245.2到任何数字，直到247-从0到1％。 在这种情况下，甚至考虑将0.01的微小变化(如245.2到245.21)添加到概率计算中。 因此，看一下图形中的第一个条，说您整天都坐着不正确，并且您的销售额将增长1％的可能性是56％。

However, it is 56% probable that your sales will move somewhere up within the range 245.2 to 247 if you keep doing what you do. It can increase 0.01% or 0.45% or 0.87%… Similarly, there is a 58% chance it will move within the range of 245.2 to 248 and so far so on.

但是，如果您继续做自己的工作，那么您的销售额很有可能在245.2到247范围内上升。 它可以增加0.01％或0.45％或0.87％...类似地，它有58％的机会会在245.2到248范围内移动，依此类推。

Therefore, be careful when interpreting this graphic!

因此，解释该图形时要小心！

正态分布 (Normal Distribution)

Finally, the Normal Distribution is the most common kind out there. Many statistical concepts and theories are based on this distribution.

最后，正态分布是最常见的一种。 许多统计概念和理论都基于这种分布。

The Normal Distribution is the famous 'bell shaped curve' where the data is distributed around the average. If you plot the values on a graphic, the mean will be the center of the curve.

正态分布是著名的“钟形曲线”，数据分布在平均值附近。 如果将值绘制在图形上，则平均值将是曲线的中心。

Knowing those qualities of that curve enables us to make many assumptions about data that are normally distributed and to calculate probabilities for a lot of things from our daily life. Extracting a sample from a population and using the statistics from that sample to understand the whole is one of the amazing advantages of the normal distribution.

知道该曲线的这些品质，使我们能够对正态分布的数据做出许多假设，并从日常生活中计算出许多事物的概率。 从总体中提取样本并使用该样本中的统计数据来了解整体是正态分布的惊人优势之一。

I believe the best analogy I know for that is with food. When you are exploring a new food or flavor, usually you don’t go for a large bite. First you get a small piece of it and try it to know the flavor. That is because you assume the whole will have the same taste of that little piece. The same is true for Normal Distributions and you can learn more about it researching about Central Limit Theorem.

我相信我所知道的最好的比喻是食物。 当您探索新的食物或风味时，通常不会大吃一口。 首先，您会得到一小块，然后尝试了解其味道。 那是因为您假设整个部分将具有与该小块相同的味道。 正态分布也是如此，您可以通过研究中心极限定理了解更多有关正态分布的信息。

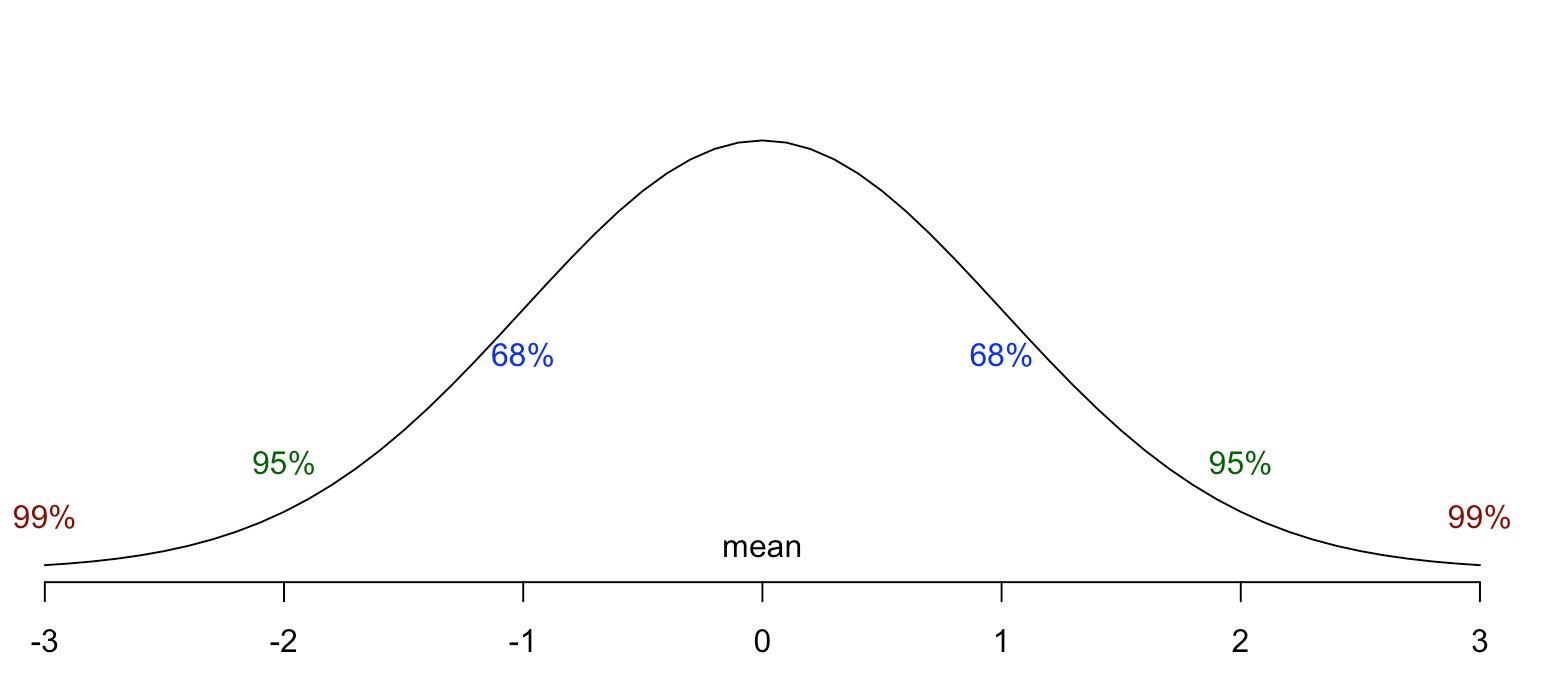
Furthermore, the area under the bell shaped curve will have 100% of the values. As the Normal Distributions are centered on its mean, it is correct to say that 50% will be higher and 50% will be lower than average, as well as most part of the values are concentrated around the average. If you calculate how much the values can be away from the center and then split the curve in 6 equal parts called standard deviation — 3 below average and 3 over the average — , each one unit of standard deviation added will hold more values.

此外，钟形曲线下方的区域将具有100％的值。 由于正态分布以平均值为中心，因此可以正确地说，平均数将比平均值高50％，而平均值将低50％，并且大多数值都集中在平均值附近。 如果计算多少的值可以从中心要离开，然后分裂在6个等份的曲线称为标准偏差-在以下的平均平均和3 3 - ，加入标准差中的每一个单元将持有多个值。

Now it becomes easier to divide the sample in ranges of probability. This is know as the 68–95–99 rule. Bear with me: looking at the normal curve below it becomes easy to see that my average is the center, the values are 3 points away from the center and we know the area under the curve comprehends 100% of the values from my sample. So if I take one standard deviation for more and one for less than the average, I will have around 68% of the values of a given attribute. If I take two standard deviations, I will have 95% of the values.And three gets me 99% of the values. And this explains the confidence interval you must have heard many times, specially during elections season. Learn more in this great video from Simple Learning Pro.

现在，将样本划分为概率范围变得更加容易。 这就是6​​8–95–99规则。 忍受我：看下面的法线曲线，很容易发现我的平均值是中心，其值与中心相距3个点，我们知道曲线下的面积包含了我样本中100％的值。 因此，如果我采用一个标准偏差多于一个标准偏差，而采用一个小于平均值的标准偏差，则将拥有给定属性值的大约68％ 。 如果我采用两个标准偏差，则将获得95％的值 ，而三个将获得99％的值。 这解释了您必须多次听到的置信区间，尤其是在选举季节。 观看来自Simple Learning Pro的精彩视频，了解更多信息。

Moving on and bringing the problem to the last ice cream example. Let’s take the month of March for our test. Here is the distribution of the 427 sales.

继续讲到最后一个冰淇淋问题。 让我们以三月份进行测试。 这是427笔交易的分布。

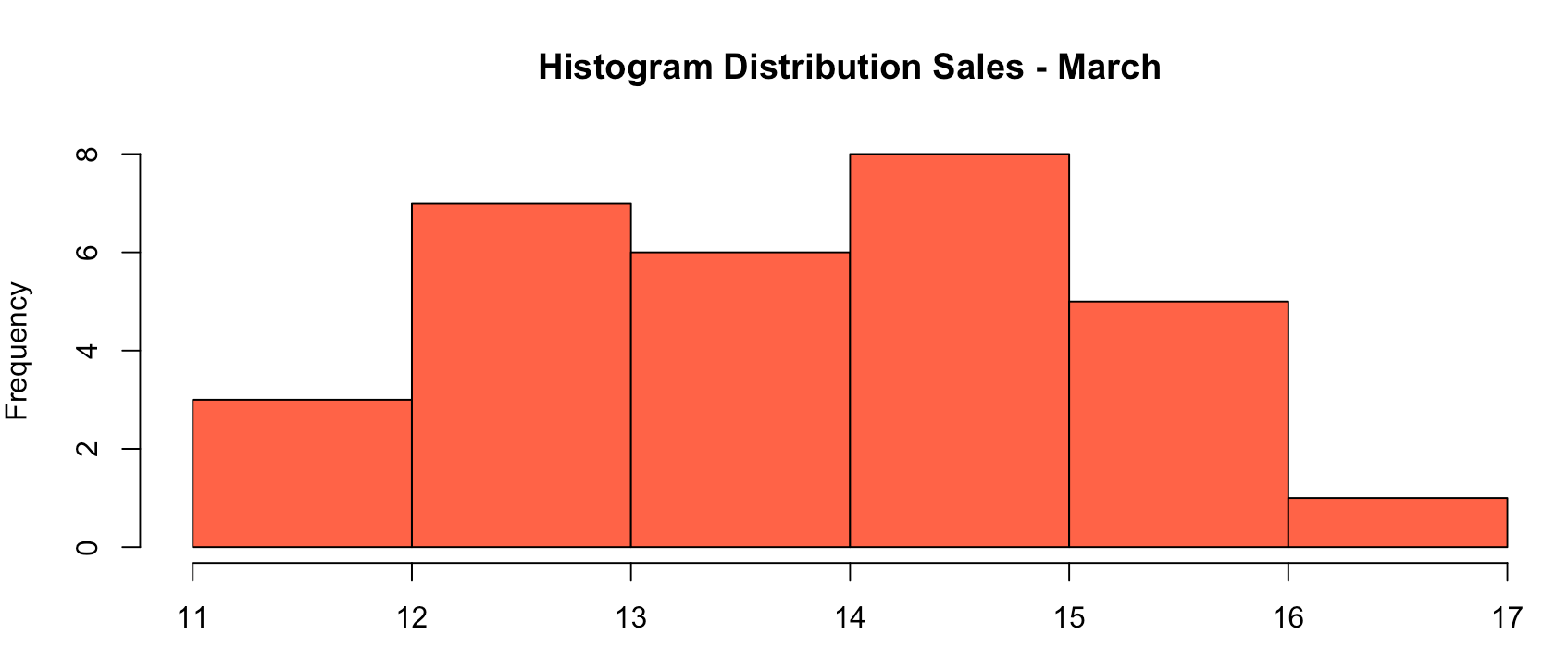
427 sales in 30 days gives us approximately 14 sales per day. The standard deviation is 1 (e.g. it could have been 13 or 15 sales instead).

在30天内实现427笔销售，使我们每天大约有14笔销售。 标准偏差是1(例如，可能是13或15次销售)。

We want to know how probable is that we have 16 sales in a day. I am multiplying by 100 so we see the final percentage already. Then we see 5% chance to have 16 sales in a day. That drops to only 0.44% if we test 17 and 0.01% for the 18 sales test.

我们想知道一天有16笔销售的可能性有多大。 我乘以100，所以我们已经看到了最终百分比。 然后，我们发现一天有16笔销售的机会为5％。 如果我们测试17，则下降到0.44％，而对于18销售测试，下降到0.01％。

# 16 sales in a day
dnorm(16, mean=14, sd=1)*100
[1] 5.399097# 17 sales in a day
dnorm(17, mean=14, sd=1)*100
[1] 0.4431848# 18 sales in a day
dnorm(18, mean=14, sd=1)*100
[1] 0.01338302

结论 (Conclusion)

The statistical tests are very useful for business and data science if we know how to apply them.

如果我们知道如何应用统计测试，则它们对于业务和数据科学非常有用。

We must have caution when showing the numbers and probabilities to the decision makers, since those can be easily misinterpreted. Be sure to always include detailed explanations for each probability and graphics.

在向决策者展示数字和概率时，我们必须谨慎行事，因为这些数字和概率很容易被误解。 确保始终包括每种概率和图形的详细说明。

It is easy to make a mistake and put the blame on 'bad' statistics. But the problem is not with the numbers, the problem is with the people interpreting those numbers.

容易犯错误并归咎于“不良”统计数据。 但是问题不在于数字，问题在于人们解释这些数字。

if data:
   data.science()

Gus

古斯