1.全排列的定义和公式:
从n个数中选取m(m<=n)个数按照一定的顺序进行排成一个列,叫作从n个元素中取m个元素的一个排列。由排列的定义,显然不同的顺序是一个不同的排列。从n个元素中取m个元素的所有排列的个数,称为排列数。从n个元素取出n个元素的一个排列,称为一个全排列。全排列的排列数公式为n!,通过乘法原理可以得到。
2.时间复杂度:
n个数(字符、对象)的全排列一共有n!种,所以全排列算法至少时间O(n!)O(n!) 的。如果要对全排列进行输出,那么输出的时间要O(n∗n!)O(n∗n!) ,因为每一个排列都有n个数据。所以实际上,全排列算法对大型的数据是无法处理的,而一般情况下也不会要求我们去遍历一个大型数据的全排列。
3.列出全排列的初始思想:
解决一个算法问题,我比较习惯于从基本的想法做起,我们先回顾一下我们自己是如何写一组数的全排列的:1,3,5,9(为了方便,下面我都用数进行全排列而不是字符)。
【1,3,5,9】(第一个)
首先保持第一个不变,对【3,5,9】进行全排列。
同样地,我们先保持3不变,对【5,9】进行全排列。
保持5不变,对9对进行全排列,由于9只有一个,它的排列只有一种:9。
故排列为【1,3,5,9】
接下来5不能以5打头了,5,9相互交换,得到
【1,3,9,5】
此时5,9的情况都写完了,不能以3打头了,得到
1,5,3,9
1,5,9,3
1,9,3,5
1,9,5,3- 1
- 2
- 3
- 4
这样,我们就得到了1开头的所有排列,这是我们一般的排列数生成的过程。再接着是以3、5、9打头,得到全排列。
我们现在做这样的一个假设,假设给定的一些序列中第一位都不相同,那么就可以认定说这些序列一定不是同一个序列,这是一个很显然的问题。有了上面的这一条结论,我们就可以同理得到如果在第一位相同,可是第二位不同,那么在这些序列中也一定都不是同一个序列。
那么,这个问题可以这样来看。对
T=【T=【 x1,x1, x2,x3,x4,x5,........xn−1,xn】x2,x3,x4,x5,........xn−1,xn】
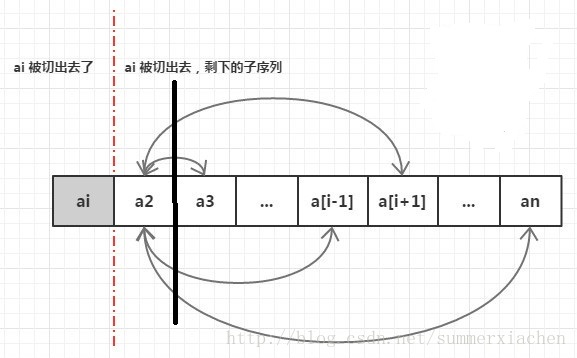
我们获得了在第一个位置上的所有情况之后(注:是所有的情况),对每一种情况,抽去序列TT 中的第一个位置,那么对于剩下的序列可以看成是一个全新的序列
T1=【x2,x3,x4,x5,........xn−1,xn】T1=【x2,x3,x4,x5,........xn−1,xn】
序列T1T1 可以认为是与之前的序列毫无关联了。同样的,我们可以对这个T1T1 进行与TT 相同的操作,直到TT 中只一个元素为止。这样我们就获得了所有的可能性。所以很显然,这是一个递归算法。
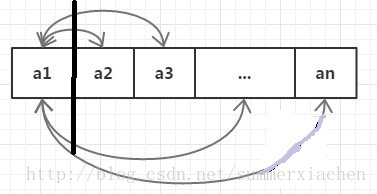
第一位的所有情况:无非是将x1x1 与后面的所有数x2,x3,.......xnx2,x3,.......xn 依次都交换一次
示意图如下:
4.全排列的非去重递归算法
算法思路:全排列可以看做固定前i位,对第i+1位之后的再进行全排列,比如固定第一位,后面跟着n-1位的全排列。那么解决n-1位元素的全排列就能解决n位元素的全排列了,这样的设计很容易就能用递归实现。
【附代码段:】
#include<iostream>
using namespace std;
int arr[5]={0,1,2,3,4};
void swap(int x,int y)//用于交换数组的两个数
{int temp=arr[x];arr[x]=arr[y];arr[y]=temp;
}
int resove(int n)//递归函数
{if(n==5)//当尝试对不存在的数组元素进行递归时,标明所有数已经排列完成,输出。{for(int i=0;i<5;i++)cout<<arr[i]; cout<<endl;return 0;}for(int i=n;i<5;i++)//循环实现交换和之后的全排列 {//i是从n开始 i=n;swap(n,i)相当于固定当前位置,在进行下一位的排列。swap(n,i);resove(n+1);swap(n,i); }}
int main()
{resove(0);
}- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
排列模板
void permutation1(char* str,int sbegin,int send) //全排列的非去重递归算法 { if( sbegin == send) //当 sbegin = send时输出 { for(int i = 0;i <= send; i++) //输出一个排列 cout << str[i]; cout << endl; } else { for(int i = sbegin; i <= send; i++) //循环实现交换和sbegin + 1之后的全排列 { swap(str[i],str[sbegin]); //把第i个和第sbegin进行交换 permutation1(str,sbegin + 1,send); swap(str[i],str[sbegin]); //【注1】交换回来 } } } - 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
【注1】swap(str[i],str[sbegin])//交换回来
我们来仔细推敲一下循环体里的代码,当我们对序列进行交换之后,就将交换后的序列除去第一个元素放入到下一次递归中去了,递归完成了再进行下一次循环。这是某一次循环程序所做的工作,这里有一个问题,那就是在进入到下一次循环时,序列是被改变了。可是,如果我们要假定第一位的所有可能性的话,那么,就必须是在建立在这些序列的初始状态一致的情况下,所以每次交换后,要还原,确保初始状态一致。
)












)


)
![[ BZOJ 4668 ] 冷战](http://pic.xiahunao.cn/[ BZOJ 4668 ] 冷战)

