You’re sitting in a classroom. You look around and see your friends writing something down. It seems they are taking the exam, and they know all the answers (even Johnny who, how to say it… wasn’t the brilliant one). You realize that your exam is in front of you, and it’s Maths. You start reading it but you don’t understand a thing. That’s terrible, your heart speeds up, you’re sweating and then… you wake up.

你坐在教室里。 您环顾四周，看到您的朋友写下来一些东西。 看来他们正在参加考试，而且他们知道所有答案(甚至Johnny谁，怎么说呢……也不是一个很棒的答案)。 您意识到考试就在眼前，这就是数学。 您开始阅读它，但您一无所知。 太糟糕了，您的心脏加速，出汗，然后……您醒来。

Uff, it was only a dream. You get back to sleep, but one thing bothers you. This paper from a dream, there was something about… how is it called… derivatives? You remember you learned it by heart at school, but never truly understood it. It’s time to face this ghost from the past.

乌夫，那只是一个梦。 您重新入睡，但一件事困扰您。 这篇梦from以求的论文，涉及到……它如何被称为…… 衍生物 ？ 您还记得自己在学校内心地学习到它，但从未真正理解过它。 现在是时候面对过去的鬼魂了。

不用担心，它在那里存在了一段时间 (Don’t be afraid, it’s there for a while)

The idea of the derivative is not new. There is a little bit of controversy about the inventor of derivatives. The battle is between Sir Isaac Newton and Gottfried Wilhelm Leibniz.

派生的想法并不新鲜。 关于衍生工具的发明者存在一些争议。 这场战斗在艾萨克·牛顿爵士和戈特弗里德·威廉·莱布尼兹之间进行。

Apparently, these two great minds discovered it independently, not being aware of their colleagues’ work. What’s interesting they came to similar conclusions having completely different ideas and approaches to the problems they were trying to solve[1].

显然，这两个伟大的思想家是独立发现它的，没有意识到他们同事的工作。 有趣的是，他们得出了相似的结论，对要解决的问题具有完全不同的想法和方法[1]。

Newton thought in the context of physics and motion, while Leibniz thought in terms of formula that could describe a change in the metaphysical meaning. However, people worked on similar theorems before the 17th century, when Newton & Leibniz lived. Arab and Persian mathematicians from the 11th and 12th centuries are supposed to discover basic ideas behind derivatives[2].

牛顿在物理和运动的语境中思考，而莱布尼兹则在可以描述形而上学意义变化的公式方面进行思考。 但是，人们在牛顿和莱布尼兹(Newton＆Leibniz)居住的17世纪之前从事类似的定理研究。 十一和十二世纪的阿拉伯和波斯数学家应该发现导数背后的基本思想[2]。

这很有用！ (And it’s useful!)

If you have ever been wondering if you’ll use any of the things you learned at school in real life, the answer is yes, derivatives are such a thing. Nowadays they are an important part of algorithms in many innovative areas, like Artificial Intelligence. In Machine Learning which is one of the AI domains, derivatives help computer programs to learn.

如果您曾经想过是否会使用在现实生活中在学校学到的任何东西，答案是肯定的，衍生工具就是这样。 如今，它们已成为人工智能等许多创新领域算法的重要组成部分。 在AI域之一的机器学习中，派生工具帮助计算机程序学习。

Generally speaking, such algorithms optimize objective functions (very often derivatives are needed for this purpose) so programs can find optimal parameters to solve different tasks (e.g. recognizing people on photos). Let’s get the key idea behind derivatives.

一般而言，此类算法会优化目标函数(为此经常需要使用导数)，因此程序可以找到最佳参数来解决不同的任务(例如，在照片上识别人物)。 让我们了解衍生工具背后的关键思想。

然而它移动 (And yet it moves)

Leibniz was right, it’s all about the change.

莱布尼兹说得对，这就是变化。

The derivative of a function gives us information about how this function is changing.

函数的导数为我们提供了有关此函数如何变化的信息。

Is it increasing? Decreasing? Or maybe it’s constant? How fast is it changing? In which direction? These are questions that depict the usefulness of derivatives. They also explain why Newton considered it in terms of the motion. Motion is also a change.

它在增加吗？ 减少？ 还是恒定的？ 它的变化速度有多快？ 朝哪个方向？ 这些是描述衍生工具有用性的问题。 他们还解释了牛顿为何以动议来考虑这一点。 运动也是一种变化。

Ok, but to understand the change of the function, we need to understand what is the function itself. So let’s do a small step back and define a function.

好的，但是要了解功能的变化，我们需要了解功能本身是什么。 因此，让我们退一步，定义一个函数。

You can imagine a function as a rule that transforms input and produces an output. It is required that such a rule can produce only one output for a given input. Putting it in other words, the function assigns one output value to each input value[3].

您可以想象一个函数通常会转换输入并产生输出。 要求这样的规则对于给定的输入只能产生一个输出。 换句话说，该函数将一个输出值分配给每个输入值[3]。

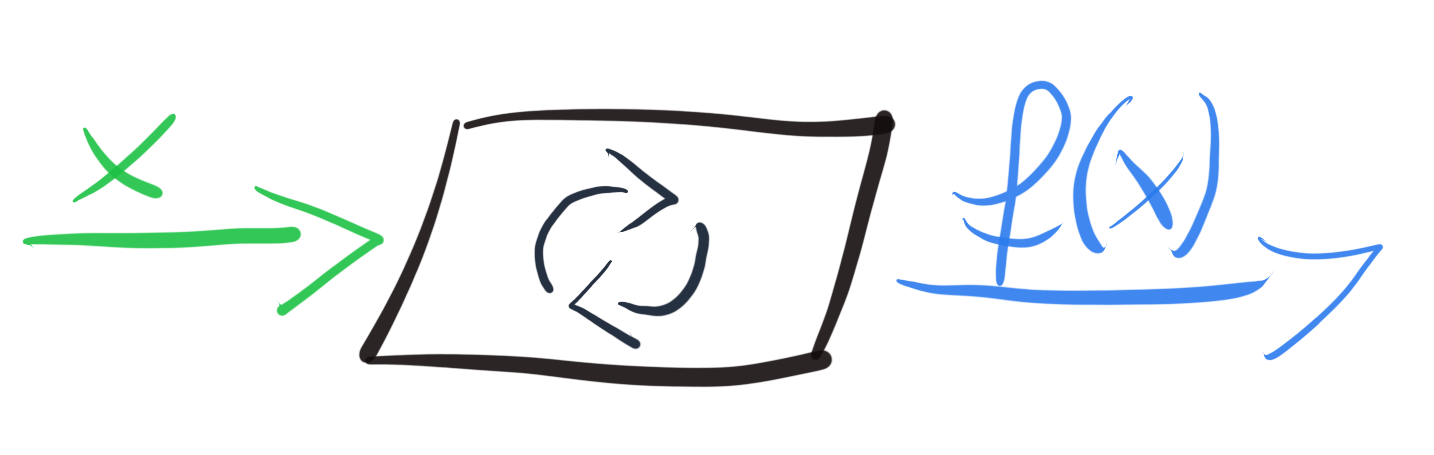
One of the simplest functions is called a linear function. Yes, it’s a straight line. Linear functions transform input number x by multiplying it by coefficient a and adding coefficient b. That’s how we compute the output of function f(x).

最简单的函数之一称为线性函数 。 是的，这是一条直线。 线性函数通过将输入数x乘以系数a并乘以系数b来变换输入数x 。 这就是我们计算函数f(x)的输出的方式。

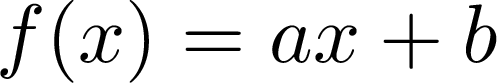
To visualize an example let’s set parameters a and b to 1. As a result we get f(x) = 1x +1. However x multiplied by 1 is x, so finally f(x) = x + 1. If we put 0 as x we get f(0) = 1, f(1) = 2 and so on. That’s the graph of our function:

为了可视化示例，我们将参数a和b设置为1。结果，我们得到f(x)= 1x +1 。 但是x乘以1就是x ，所以最终f(x)= x + 1 。 如果将0设为x，我们得到f(0)= 1 ， f(1)= 2等等。 那是我们函数的图形：

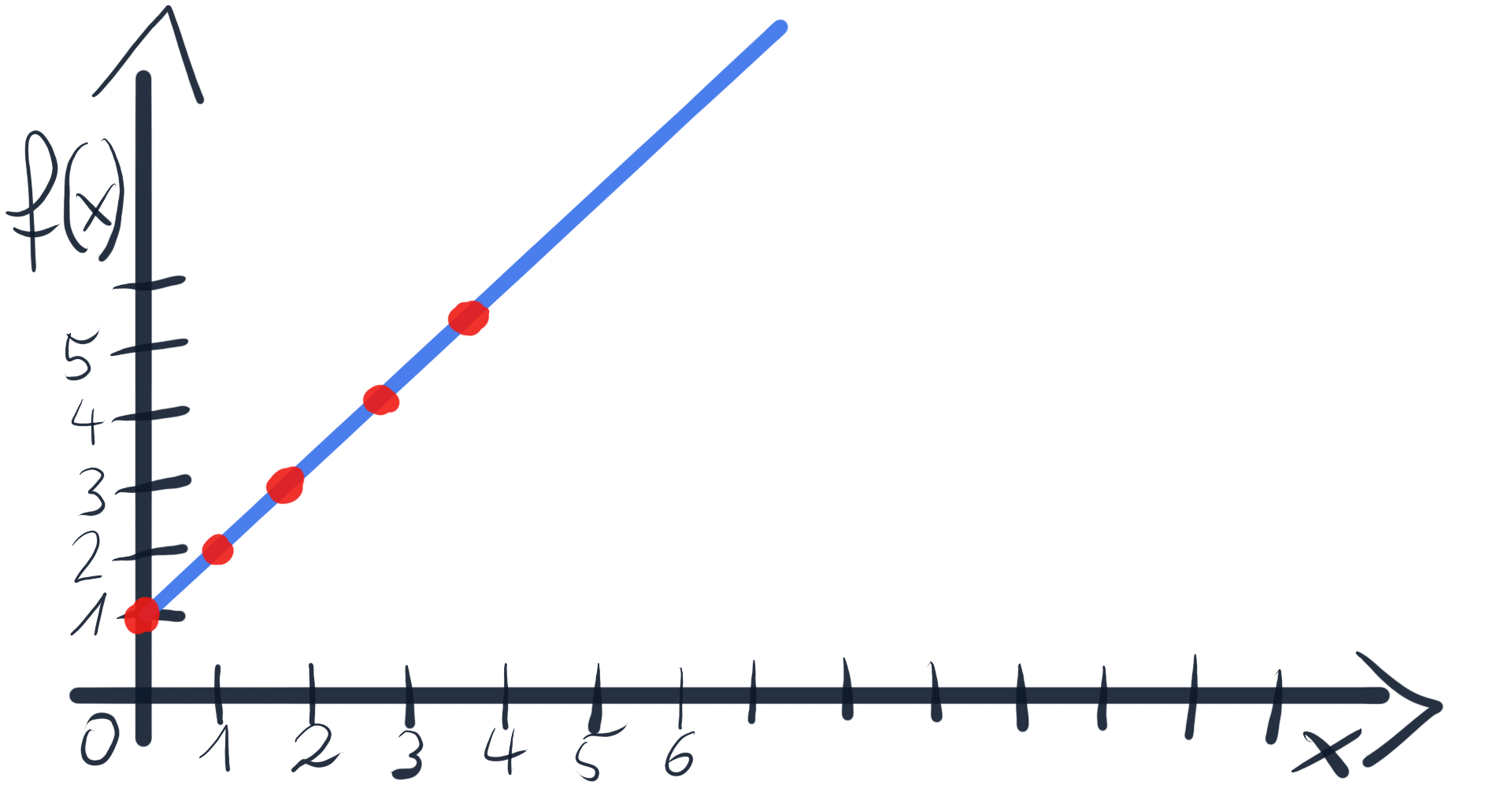
Having in mind the key idea about derivatives and functions, let’s put it all together. We’ll see how derivative describes changes of our linear function f(x).

考虑到有关派生和函数的关键思想，让我们将它们放在一起。 我们将看到导数如何描述线性函数f(x)的变化 。

增长还是衰减？ (Growth or decay?)

To determine the change of our function f(x) = x + 1, we can take a look at its graph and calculate what’s the change on the vertical axis when the value on the horizontal axis (x) changes by one unit.

为了确定函数f(x)= x + 1的变化 ，我们可以看一下它的图，并计算水平轴(x)的值变化一个单位时垂直轴的变化。

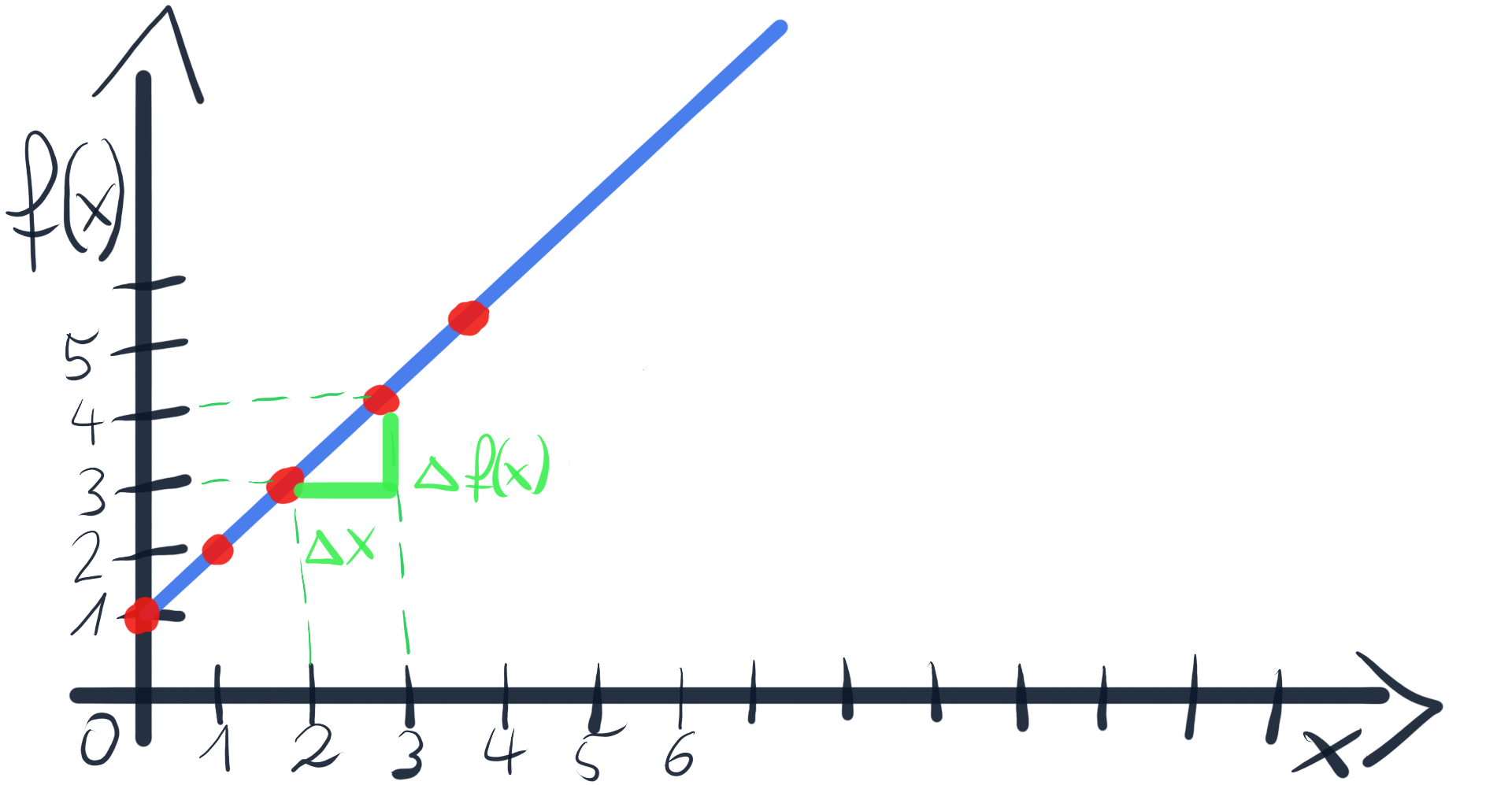
As you can see in the picture, if we change x by 1 (Δx = 1), it results in grow of f(x) by 1 (Δf(x) = 1). Our line is going up, it’s increasing. And that’s exactly what a parameter tells us (a = 1).

如您在图片中看到的，如果我们将x改变1( Δx= 1 )，则会导致f(x)增长1( Δf(x)= 1 )。 我们的生产线正在上升，正在增加。 而这正是一个参数告诉我们(A = 1)。

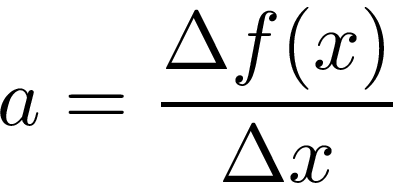
If a would be negative, for example, a = -1, our line would go down. And the function would decrease by 1 unit per 1 unit change of x.

如果a为负，例如a = -1 ，则我们的行将下降。 并且每x改变1个单位，该函数将减少1个单位。

But what happens when our function is not a line, but a curve? In such cases, we need to check how our function is changing at each point that is interesting for us. The curve can increase, decrease, or be constant in different areas of the space.

但是，当我们的功能不是直线而是曲线时会发生什么呢？ 在这种情况下，我们需要检查我们感兴趣的每个点的功能如何变化。 曲线可以在空间的不同区域中增加，减少或保持不变。

To check the change of function in a given point we can think of tangent in this point of the curve (green line) and the a coefficient of this tangent. It has information about the change.

要检查给定点的函数变化，我们可以考虑曲线的该点(绿线)的切线和该切线的系数。 它具有有关更改的信息。

统治一切的规则 (Rules to rule them all)

Graphs are a really useful form of visualizing functions, however, in more complex scenarios it’s not easy to plot a graph. Functions can have more dimensions than we’re able to see and imagine. Finally, sometimes it’s just easier to calculate the derivative that plot the function.

图形是可视化功能的一种非常有用的形式，但是，在更复杂的场景中，绘制图形并不容易。 函数的维度超出我们所能看到和想象的范围。 最后，有时更容易计算出绘制函数的导数。

Fortunately, there is a set of rules we can use to calculate derivatives. Let’s introduce 3 simple yet useful ones.

幸运的是，我们可以使用一组规则来计算导数。 让我们介绍3个简单而有用的方法。

常数的导数 (The derivative of a constant)

Constant means no change at all. As a result, the derivative of something constant is equal to zero. As simple as that. This idea is compatible with our considerations regarding a coefficient of a linear function.

常数表示完全没有变化。 结果，常数的导数等于零。 就如此容易。 这种想法与我们有关的线性函数的系数考虑兼容。

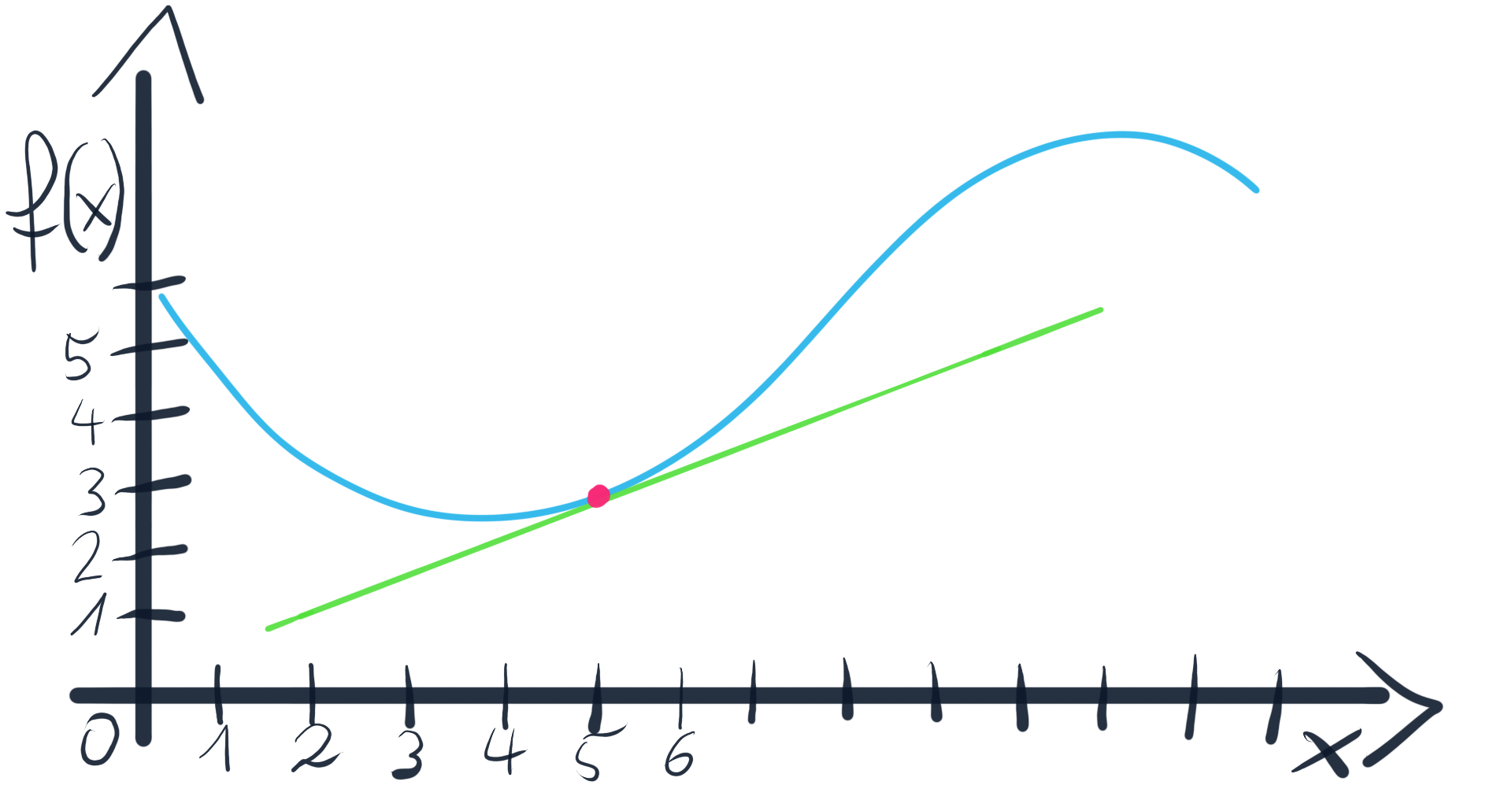
If a = 0, the only things that is left in the function is parameter b, so f(x) = b. And b is a constant number like 4. Let’s have a look at the graph:

如果a = 0，则函数中仅剩下参数b ，因此f(x)= b 。 b是一个像4的常数。让我们看一下图：

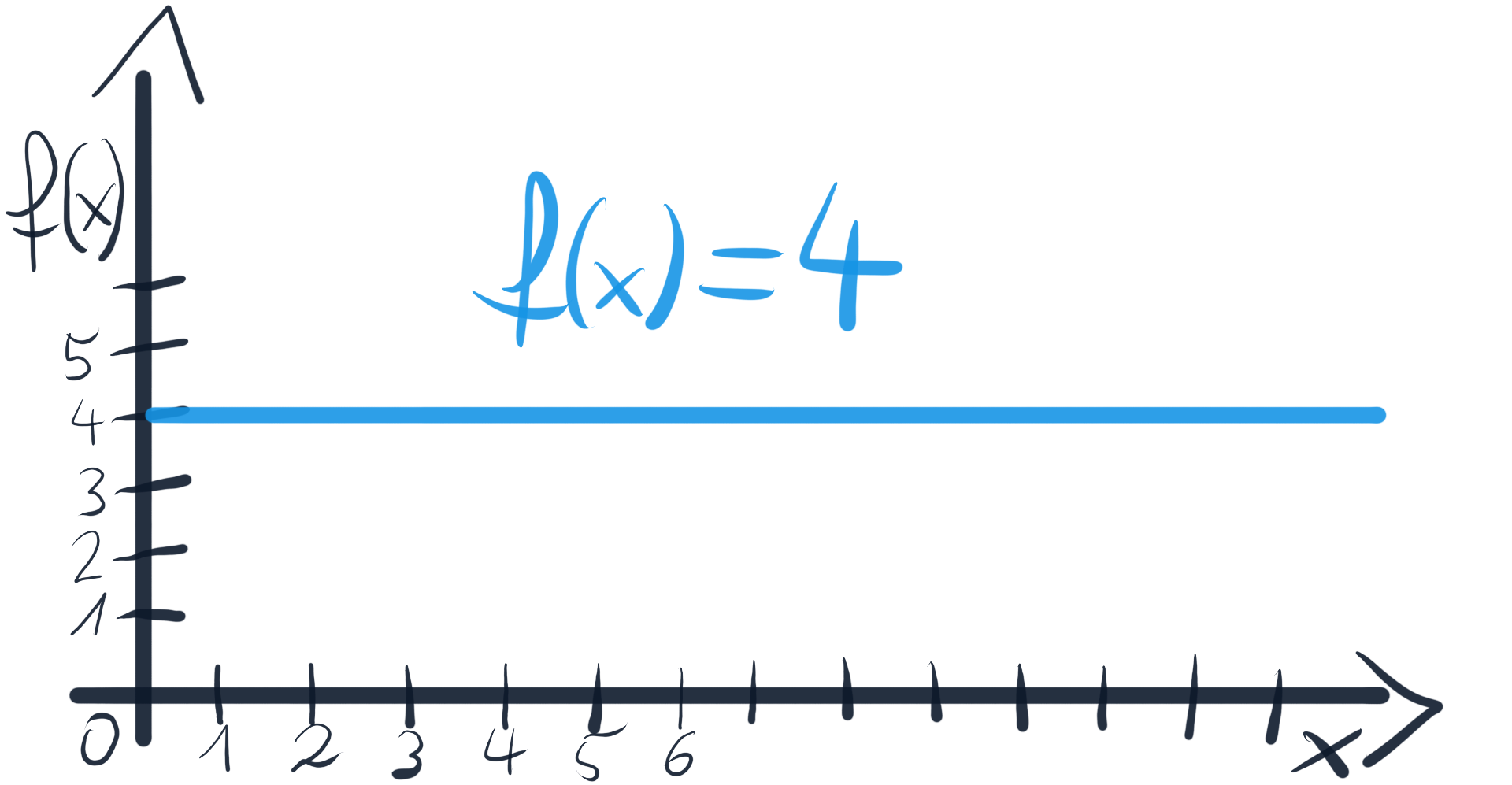
Extremely stable, isn’t it?

非常稳定，不是吗？

幂的导数 (The derivative of a power)

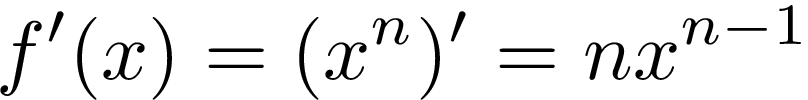
Calculating the derivative of a power is also very simple. Having function f(x)=xⁿ, we put n before x and raise x to the power of n-1. Symbol f ’(x) means the derivative of function f(x). For example:

计算幂的导数也非常简单。 有函数f(x)=xⁿ，我们n放在x和加薪十大之前N-1的能力。 符号f'(x)表示函数f(x)的导数。 例如：

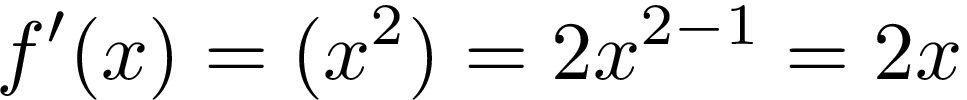
Actually, this function is a parabola:

实际上，此函数是抛物线：

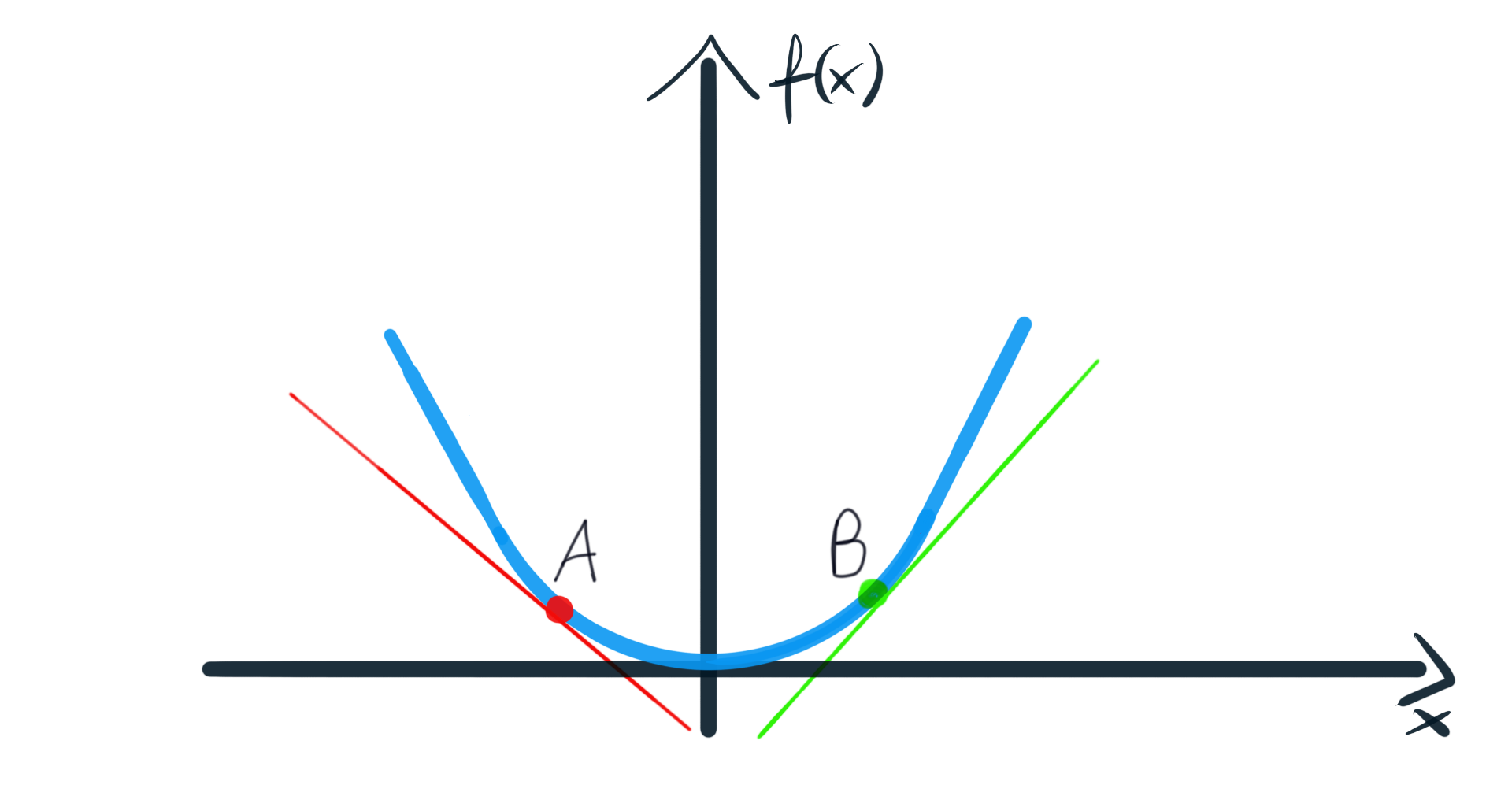
In point A a derivative will be negative, because the tangent slope is decreasing. Our parabola goes through (0, 0), so in point A (to the left of 0) x will be negative, e.g. -5. We can calculate it:

在点A上 ，导数将为负，因为切线斜率正在减小。 我们的抛物线穿过(0，0)，因此在点A (位于0的左侧) x为负，例如-5。 我们可以计算出：

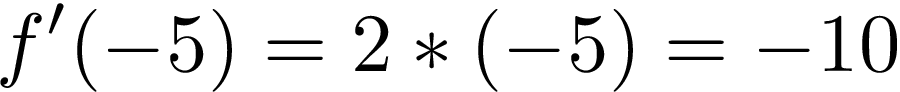
When we choose point B on the other side of the axis, x = 5, we see that tangent line is going up. Derivative at this point should be positive. Let’s check it:

当我们选择轴另一侧的B点x = 5时 ，我们会看到切线在上升。 此时的导数应为正。 让我们检查一下：

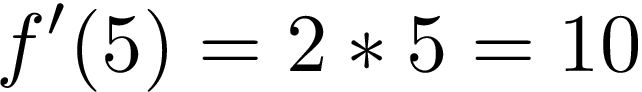
连锁规则 (Chain rule)

It sounds a little bit spooky, chains, ghosts, etc. Ok, it’s the most complex rule we learn today, but no worries, we’ll follow a simple example.

听起来有点怪异，连锁，鬼影等。好的，这是我们今天学习的最复杂的规则，但不用担心，我们将举一个简单的例子。

Chain rule is useful when we need to calculate a derivative of so-called composite functions. You can imagine a composite function, as a function that includes another function inside. To spark your imagination even more, composite functions are like Russian dolls.

当我们需要计算所谓的复合函数的导数时，链式规则很有用。 您可以将复合函数想象为内部包含另一个函数的函数。 为了激发您的想象力，复合功能就像俄罗斯的娃娃一样。

Having function f that contains function g is f(g(x)). We calculate the derivative of function f using this formula:

具有包含函数g的函数f是f(g(x))。 我们使用以下公式计算函数f的导数：

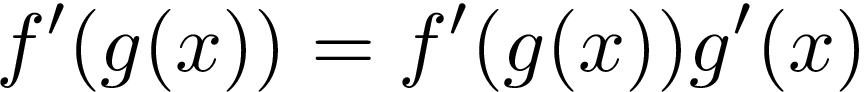
Let’s decipher it. The first part of a chain rule says that we have to calculate a derivative of a function f’(g(x)), so the derivative of an “outside” function. Then we have to multiply it by a derivative of an inner function g’(x).

让我们破译它。 链式规则的第一部分说，我们必须计算函数f'(g(x))的导数，因此必须计算“外部”函数的导数。 然后，我们必须将其乘以内部函数g'(x)的导数 。

An example will shed some light on these chains. Let’s have a function g(x) = x² and function f(g(x)) = (x²)². It’s equal to x⁴ and using the power rule we know that (x⁴)’ is equal to 4x³. But for the sake of example let’s calculate it using the chain rule and check if we get the same result.

一个例子将阐明这些链条。 让我们有一个函数g(x)=x²和函数f(g(x))=(x²)² 。 它等于x⁴，并且使用幂定律我们知道(x⁴) '等于4x³ 。 但是为了举例，让我们使用链式规则进行计算，并检查是否得到相同的结果。

So the first step is to calculate the derivative of the outer function f’(g(x)), in our case it’s (g(x))². So we use a power rule and we get:

因此，第一步是计算外部函数f'(g(x))的导数 ，在本例中为(g(x))² 。 因此，我们使用幂规则，得到：

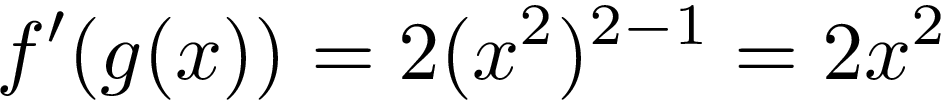
The second step is to calculate the derivative of the inner function g(x), let’s use power rule again:

第二步是计算内部函数g(x)的导数，让我们再次使用幂规则：

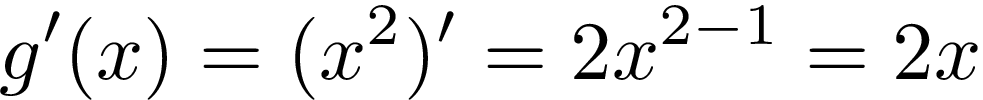
Finally, we have to multiply the derivative of an outer function by derivative of an inner function:

最后，我们必须将外部函数的导数乘以内部函数的导数：

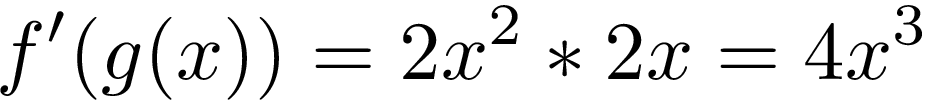
Yes! We got the same result as for using the power rule. It means our chain rule works!

是! 我们得到的结果与使用幂规则相同。 这意味着我们的连锁规则有效！

用它！ (Use it!)

Now, you got the intuition as well as simple mathematical apparatus you can use in practice. If you’re interested in Artificial Intelligence you can use this knowledge to get a more in-depth understanding of Machine Learning algorithms (e.g. Gradient Descent).

现在，您已经获得了直觉以及可以在实践中使用的简单数学工具。 如果您对人工智能感兴趣，则可以使用此知识对机器学习算法(例如Gradient Descent )有更深入的了解。

If you’re not into AI at all, but you love puzzles (Sudoku, crosswords), I encourage you to grab some Math book and play by calculating derivatives. It’s a great brain training and you’ll get addicted to solving more and more challenging examples.

如果您根本不喜欢AI，但是您喜欢拼图(数独，填字游戏)，那么我建议您拿些数学书，并通过计算导数来玩。 这是一次很棒的大脑训练，您将沉迷于解决越来越多具有挑战性的示例。

If these ideas don’t appeal to you, you still gained knowledge about one of the very important Mathematics tool, widely used in many domains. You won’t be surprised when you meet derivatives someday in the future.

如果这些想法对您没有吸引力，您仍然会获得关于在许多领域中广泛使用的非常重要的数学工具之一的知识。 将来某天遇到衍生产品时，您不会感到惊讶。

参考书目 (Bibliography)

1. https://www.math.uh.edu/~tomforde/calchistory.html

   https://www.math.uh.edu/~tomforde/calchistory.html

2. https://en.wikipedia.org/wiki/History_of_calculus

   https://zh.wikipedia.org/wiki/History_of_calculus

3. Stroud K.A., Booth Dexter J., Engineering Mathematics, ISBN: 978–0831133276.
   斯特劳德·卡(Stroud KA)，布斯·德克斯特(Booth Dexter J.)，工程数学，ISBN：978–0831133276。